【考后总结】NOI 春季测试 2023
文化课补完了，所以来改题。
T1 涂色 paint
弱智签到题，维护时间戳。
提交记录：Submission - QOJ
T2 幂次 power
一个数可能会被统计多次，例如 \(2^{12}=4^6=8^4=16^3=64^2\)，考虑只在 \(2^{12}\)，即指数最大的位置记录答案，由于 \(1\) 比较特殊先不考虑。
可以得到 \(cnt_i=\left\lfloor\sqrt[i]{n}\right\rfloor-1\)，表示可以表示为 \(x=a^i\) 的个数。
于是要在 \(i\) 处删去 \(i\times j\) 次的贡献，也就是减去所有倍数的并，容斥：
显然多重集没有贡献，容斥系数是 \(\mu\)，集合交的大小也就是对应的 \(cnt\)。
提交记录：Submission - QOJ
这个复杂度在 CodeForces 里过不去，原因是单次 \(O(\log^2 n)\) 不够快。
容易发现 \(k\ge 3\) 时数据规模较小，可以暴力枚举底数和指数，并且这个支持预处理。
\(k=2\) 的部分可以用 \(\left\lfloor\sqrt{n}\right\rfloor\) 求出，但有重复部分，重复部分可以在暴力枚举 \(k\ge 3\) 时不统计指数为偶数的情况。
T3 圣诞树 tree
任意选四个点构成一个四边形，走对角线一定不是最优策略，同样路径也不能出现交叉。
这说明对于已经走到的区间 \([L,R]\) 下一个要去到的位置一定是 \(L-1\) 或 \(R+1\)，区间 DP 一下。
提交记录：Submission - QOJ
T4 密码锁 lock
\(k=1\)
直接输出最大值减最小值。
\(k=2\)
容易发现把较小值放一行把较大值放一行一定不劣。
\(k=3\)
和 \(k=2\) 关系不大。
直接求不好求所以考虑二分答案，目前二分的极差为 \(mid\)。
所有数中的最大值和最小值放在一行一定最劣，所以我们相当于已经确定一行的最大值和一行的最小值了，那么对于每一列都可以 \(O(k)\) 判断当前这个顺序是不是能满足条件，具体就是看与最大值一行的是不是不小于 \(mx-mid\)，与最小值一行的是不是不大于 \(mn+mid\)。
而剩下一行实际上是一个值域的问题，假设当前枚举的列在剩下一行的值为 \(x\)，那么这个值适用于最小值在 \([x-mid,x]\) 内的情况，区间加，只需要判断是否存在一个位置被加了 \(n\) 次。还剩一个问题是一列可能不只有一种放置方法是满足条件的，但这几种放置方法对 \([x-mid,x]\) 的贡献不能同时存在，所以需要对每一列的贡献区间求并集再差分。
钦定最大值在第一行，最小值在第二行和第三行是不同的，需要枚举。
这样单次判断的复杂度是 \(O(nk)\)，总复杂度 \(O(nk^2\log a)\)。
\(k=4\)
\(k=3\) 做法放到 \(k=4\) ，正解就呼之欲出了！
把一维的线段加改成矩形加，线段求并改成矩形求并，剩下就是一个扫描线。
需要思考的是如何把一列 \(O(k)\) 个矩形求并，直接容斥的 \(O(2^k)\) 不够优秀，可以考虑把矩形拆成多个。
一个拆法是把纵坐标离散化，把每个纵坐标区间的矩形单独拿出来，类似一个线段求并。但问题是我们把答案记在了矩形的每个整点上，这样会出现矩形边界被计算两侧或矩形实际上是线段而没有被计入。在此基础上修改，可以把每个矩形边界单独拿出来，剩下纵坐标区间改成开区间，但矩形个数增加，常数变大了。
一个好的解决方法如下：
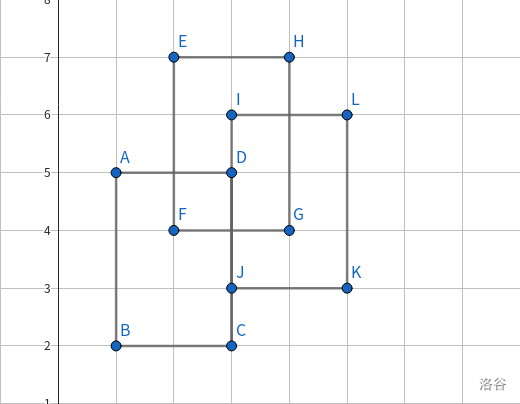
对于一个 \(x\in [l,r],y\in [u,d]\) 的矩形，由于横向是线段处理，不做改变，而纵向改成 \([u-1,d]\)，这样相当于把整点 \((x,y)\) 的答案记在了正下方的方格上，这时候再对矩形求并方格一定不会算重，同时也就规避掉了矩形本身是线段的情况。加入扫描线时再把 \(u\) 加回来即可。
这样单次判断的复杂度是 \(O(nk^2\log a)\)，总复杂度是 \(O(nk^3\log^2 a)\)，可以通过。（算复杂度可能把部分展开的循环也计算在内了。）
提交记录：Submission - QOJ
