【学习笔记】Segment Tree Beats
基础线段树操作的复杂度证明
单点操作
由于线段树深度是 \(O(\log n)\),同一层只会去到一个节点,复杂度是 \(O(n\log n)\)。
区间查询
按照当前所在区间 \([l,r]\) 与询问区间 \([L,R]\) 分成三种情况:
-
\([l,r]\) 与 \([L,R]\) 无交,退出函数。
-
\([l,r]\) 是 \([L,R]\) 的子区间,更新答案并退出函数。
-
除上面两种情况以外的,向下递归。
注意到前两种情况一定来自于第三种情况,且数量不会超过第三种情况的 \(2\) 倍,只需要考虑第三种情况。
对线段树每层进行考虑,出现第三种情况一定是在可以遍历到的区间中左右两个,因此每一层只有 \(O(1)\) 个第三种情况,故 \(O(\log n)\) 的复杂度是 \(O(\log n)\)。
区间修改
打上懒标记之后,算法流程同区间查询。
合并
设初始线段树总节点数为 \(m\),注意到每合并一个节点相当于减少一个节点,因此复杂度是 \(O(m)\),通常是 \(O(n\log n)\)。
区间最值操作
区间最值操作指对 \(i\in [l,r]\),\(a_i\leftarrow \max/\min(a_i,k)\) 的操作。
不含区间加减的问题
支持区间取 \(\min\),区间求 \(\max\),区间求和。
算法流程
对每个节点维护最大值 \(mx\),严格次大值 \(secmx\),最大值个数 \(cntmx\),和 \(sum\) 以及标记 \(tag\)。
当前区间是修改区间子区间时,与 \(k\) 取 \(\min\) 时进行讨论:
-
若 \(mx<k\),则操作不会影响到这个节点以及其子树,退出函数。
-
若 \(secmx<k\le mx\),则操作只会影响到最大值,\(sum\leftarrow sum+cntmx\times(k-mx),mx\leftarrow k,tag\leftarrow k\),退出函数。
-
若 \(secmx\ge k\),向下递归修改。
下传标记时类似类似,注意到打标记的前提条件,因此下传只有前两种情况。
点击查看代码
int t;
int n,m;
int a[maxn];
struct SegmentTree{
#define mid ((l+r)>>1)
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
int mx[maxn<<2],secmx[maxn<<2],cntmx[maxn<<2];
ll sum[maxn<<2];
int tag[maxn<<2];
inline void push_up(int rt){
if(mx[rt<<1]==mx[rt<<1|1]){
mx[rt]=mx[rt<<1],secmx[rt]=max(secmx[rt<<1],secmx[rt<<1|1]),cntmx[rt]=cntmx[rt<<1]+cntmx[rt<<1|1];
sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}
else if(mx[rt<<1]>mx[rt<<1|1]){
mx[rt]=mx[rt<<1],secmx[rt]=max(secmx[rt<<1],mx[rt<<1|1]),cntmx[rt]=cntmx[rt<<1];
sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}
else{
mx[rt]=mx[rt<<1|1],secmx[rt]=max(mx[rt<<1],secmx[rt<<1|1]),cntmx[rt]=cntmx[rt<<1|1];
sum[rt]=sum[rt<<1]+sum[rt<<1|1];
}
}
void build(int rt,int l,int r){
tag[rt]=-1;
if(l==r){
mx[rt]=a[l],secmx[rt]=-1,cntmx[rt]=1;
sum[rt]=a[l];
return;
}
build(lson),build(rson);
push_up(rt);
}
inline void push_down(int rt){
if(tag[rt]!=-1){
if(mx[rt<<1]>tag[rt]&&secmx[rt<<1]<tag[rt]){
sum[rt<<1]+=1ll*cntmx[rt<<1]*(tag[rt]-mx[rt<<1]),mx[rt<<1]=tag[rt];
tag[rt<<1]=tag[rt];
}
if(mx[rt<<1|1]>tag[rt]&&secmx[rt<<1|1]<tag[rt]){
sum[rt<<1|1]+=1ll*cntmx[rt<<1|1]*(tag[rt]-mx[rt<<1|1]),mx[rt<<1|1]=tag[rt];
tag[rt<<1|1]=tag[rt];
}
tag[rt]=-1;
}
}
void update_min(int rt,int l,int r,int pl,int pr,int k){
if(pl<=l&&r<=pr){
if(mx[rt]<=k) return;
else if(secmx[rt]<k){
sum[rt]+=1ll*cntmx[rt]*(k-mx[rt]),mx[rt]=k;
tag[rt]=k;
return;
}
}
push_down(rt);
if(pl<=mid) update_min(lson,pl,pr,k);
if(pr>mid) update_min(rson,pl,pr,k);
push_up(rt);
}
int query_max(int rt,int l,int r,int pl,int pr){
if(pl<=l&&r<=pr) return mx[rt];
push_down(rt);
int res=0;
if(pl<=mid) res=max(res,query_max(lson,pl,pr));
if(pr>mid) res=max(res,query_max(rson,pl,pr));
return res;
}
ll query_sum(int rt,int l,int r,int pl,int pr){
if(pl<=l&&r<=pr) return sum[rt];
push_down(rt);
ll res=0;
if(pl<=mid) res+=query_sum(lson,pl,pr);
if(pr>mid) res+=query_sum(rson,pl,pr);
return res;
}
#undef mid
#undef lson
#undef rson
}S;
int main(){
t=read();
while(t--){
n=read(),m=read();
for(int i=1;i<=n;++i) a[i]=read();
S.build(1,1,n);
for(int i=1;i<=m;++i){
int opt=read(),l=read(),r=read();
if(!opt){
int k=read();
S.update_min(1,1,n,l,r,k);
}
else if(opt==1) printf("%d\n",S.query_max(1,1,n,l,r));
else printf("%lld\n",S.query_sum(1,1,n,l,r));
}
}
return 0;
}
复杂度证明
定义一个节点的标记为这个节点子树内的最大值,并删去和父亲标记相同的所有标记,这样初始标记有 \(O(n)\) 个,且满足由上到下递减的性质,具体如下图:
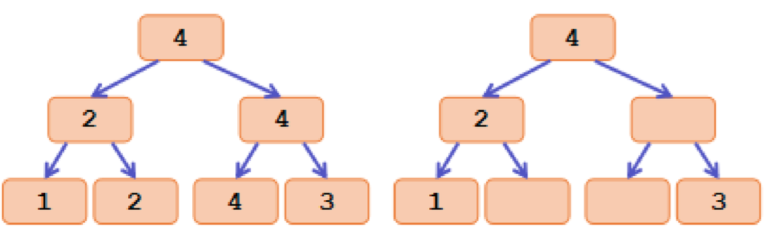
另一性质是,节点的严格次大值等价于子树内(不包含本身)中标记的最大值。
定义一类标记为一次修改以及对应懒标记下传时得到的标记,定义一类标记的权值为子树内含有这类标记的节点个数,定义势能函数 \(\Phi(x)\) 为所有标记的权值总和。
初始 \(\Phi(x)\) 为 \(O(n\log n)\) 级别。
把取 \(\min\) 操作遍历的节点为两种:常规操作也会遍历到的以及暴力向下递归的,每次操作前者个数为 \(O(\log n)\)。同时懒标记下传时最多影响 \(2\) 个区间,每次下传伴随线段树的遍历,在常规遍历中共下传 \(O(m\log n)\) 次。这样可以证明常规遍历以及伴随的下传懒标记的复杂度都是 \(O(m\log n)\)。
考虑暴力向下递归的节点,暴力向下递归意味着子树内存在小于 \(k\) 的标记,向下递归等价于回收的这个不合法的标记。这样每遍历到一个节点就意味着这个子树内至少有一个标记被回收,对应这个标记在当前节点产生的权值就会减少,因此每遍历到一个节点 \(\Phi(x)\) 至少减少 \(1\),而 \(\Phi(x)\) 不超过 \(O((n+m)\log n)\) 级别,暴力向下递归执行的次数也不超过 \(O((n+m)\log n)\) 级别。
总复杂度是 \(O((n+m)\log n)\)。
包含区间加减的问题
区间加减对维护的 \(mx,secmx,cntmx,sum\) 影响不大,可以按照相同方法处理。
复杂度证明略有不同,修改势能函数 \(\Phi(x)\) 的定义,定义其为每个标记所在节点的深度和。
在暴力递归时,节点的原有标记在由父亲下传后一定会被立刻撤去,所以这里的下传不会产生影响。常规操作的下传相当于增加 \(O(\log n)\) 个节点存在标记,那么深度和 \(\Phi(x)\) 增加 \(O(\log^2 n)\)。区间加减的操作同理,也是增加 \(O(\log n)\) 个节点存在标记。
暴力递归的分析和上面类似,遍历到删去一个标记的过程均摊就是每遍历一个节点 \(\Phi(x)\) 减少 \(1\),这样总复杂度可以分析到 \(O(m\log^2 n)\)。
实际跑得很快。
发现在复杂度分析过程中,并没有实际用到区间加减这操作,所以区间赋值之类不影响 \(mx,secmx,cntmx,sum\) 的操作都是可以的。
参考资料
-
《区间最值操作与历史最值问题》 - 吉如一


 浙公网安备 33010602011771号
浙公网安备 33010602011771号