【学习笔记】多项式 1:基础操作
复数
以下内容均在高中数学范围。
复数的定义与运算
定义 \(i=\sqrt{-1}\),称 \(z=a+bi\) 为 复数,复数集用 \(\mathbf{C}\) 表示。
复数的四则运算:
复平面
定义复平面横轴为实数,纵轴为虚数,点 \((a,b)\) 唯一对应复数 \(z=a+bi\)。
引入复平面上的向量,起点为原点,终点为 \((a,b)\),将相关定义补充至复数的概念当中。
定义复数 \(z=a+bi\) 的 模 为该向量的模长 \(|z|=\sqrt{a^2+b^2}\),辐角 \(\theta=\mathrm{Arg} z=\mathrm{arctan} \tfrac{b}{a}+2k\pi\ (k\in \mathbb{Z})\),满足 \(\theta\in [-\pi,\pi]\) 的 \(\theta\) 称为 辐角主值,记作 \(\mathrm{arg} z\)。
若复数的模为 \(r\),辐角为 \(\theta\),则同样可以将复数 \(z\) 表示为 \(r(\cos\theta+i\sin\theta)\)。
棣莫佛定理
因此若干复数累乘表现为 模累乘,辐角累加。
同时当 \(r=1\) 时,模不变,因此单位圆上的复数乘法等价于逆时针旋转 \(\theta\)。
单位根
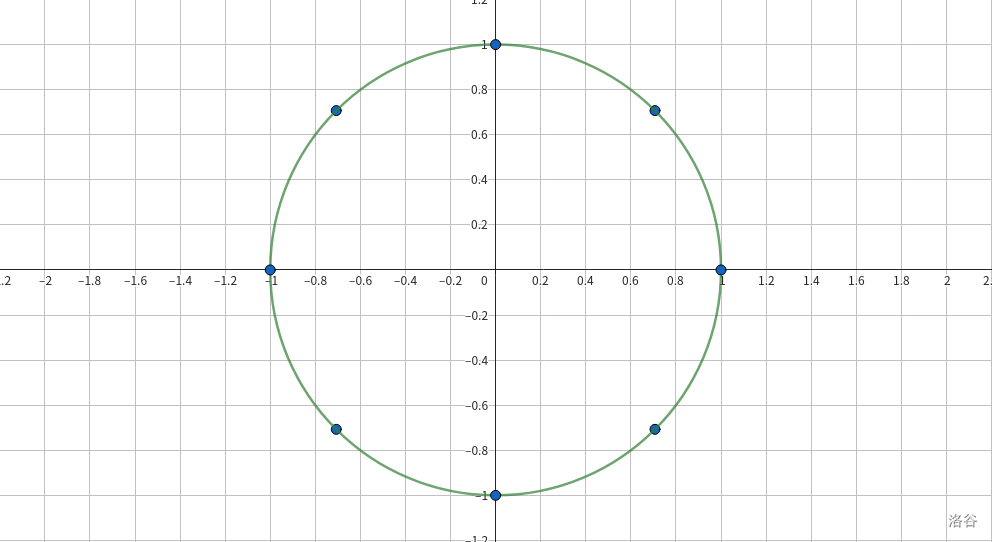
当棣莫佛定理中的复数均相同且 \(r=1\) 时,\(z^n\) 就表现为从 \((1,0)\) 开始每次旋转 \(\theta\),若 \(\theta=\dfrac{2k\pi}{n}\ (k\in[0,n))\),则旋转 \(n\) 次后恰好回到 \((1,0)\)。定义此时的复数 \(z\) 为 \(n\) 次单位根,记作 \(\omega_n\),同时 \(n\) 个单位根也是方程 \(x^n-1=0\) 的全部解。而任意的单位根都能被最小单位根(即第一次逆时针旋转得到的单位根) \(\omega_{n}\) 的乘方表示。
单位根具有很多性质,列举其中的部分:
-
\(\omega_{n}^k=\omega_{n}^{k\bmod n}\) 显然 \(n\) 次为一循环。
-
\(\omega_{cn}^ck=\omega_{n}^k\) 代入定义式中可消去 \(c\)。
-
\(\omega_{n}^k\ (\gcd(n,k)=1)\) 的 \(0\sim i-1\) 次幂各不相同,称这些单位根为 \(n\) 次本原单位根。这等价于数论中的欧拉定理,底数与模数互质时构成了完全剩余系,而此时的底数即为单位根,模数即为循环大小 \(n\)。
欧拉公式
证明略。
多项式基本概念与性质
基本定义
称形如 \(f(x)=\sum_{i=0}^n a_ix^i\) 的 有限和式 为 多项式,其中 \(a_i\) 为 \(i\) 次项的 系数,记作 \([x^i]f(x)\),其中系数非零的最高次项的次数 \(i\) 称作多项式的 度,也称作 次数,记作 \(\mathrm{deg} f\)。
若项数无限,形如 \(\sum_{i=0}^{\infty}a_ix^i\) 的多项式称为 形式幂级数。
使得 \(f(x)=0\) 的 \(x\) 被称为多项式的 根。
代数基本定理:一个 \(n\) 次多项式至少有一个互异的根,恰好有 \(n\) 个两两可能重复的根。
表示方法
多项式的两种表示方法:系数表示法 与 点值表示法。系数表示法即给出所有的 \(a_i\);将 \(x=x_i\) 代入 \(f(x)\) 得到 \(y_i=f(x_i)\),用若干点值 \((x_i,y_i)\) 表示多项式的方法称为点值表示法。
系数表示法转为点值表示法称为 求值,点值表示法转为系数表示法称为 插值。
由于 \(n\) 个 \(n\) 元线性方程构成的方程组有唯一解,则任意 \(n\) 个点值即可解出 \(n-1\) 次多项式的 \(n\) 个系数。所以:\(n\) 个点值可以唯一确定 \(n-1\) 次的多项式。
基本运算
定义 \(\Delta^n f(x)=\Delta^{n-1} f(x+1)-\Delta^{n-1} f(x)\) 为 \(f(x)\) 的 \(n\) 阶差分,其中 \(\Delta^0 f(x)=f(x)\)。
\(n\) 次多项式的 \(k\) 阶差分是 \(n-k\) 次多项式,因此 \(k\) 阶差分为 \(n\) 次多项式的多项式是 \(n+k\) 次多项式。
多项式乘法:\(n\) 次多项式 \(f(x)=\sum_{i=0}^n a_ix^i\) 与 \(m\) 次多项式 \(g(x)=\sum_{i=0}^m b_ix^i\) 的卷积 \(h=f*g\) 定义为:
因此 \(h(x)\) 应为 \(n+m\) 次多项式。
拉格朗日插值
常规拉格朗日插值
常规的解线性方程组需要使用高斯消元法,复杂度为 \(O(n^3)\)。
拉格朗日插值是一种使用构造得出多项式的方法。
类比中国剩余定理中的构造,如果我们能够构造出 \(n\) 个多项式 \(f_i(x)\),使得 \(f_i(x_i)=y_i,f_i(x_j)=0\ (i\neq j)\),那么这 \(n\) 个多项式之和即为所求的多项式。
当 \(i\neq j\) 时使 \(f_i(x_j)=0\) 不难想到 \(\prod_{j\neq i} (x-x_j)\) 的构造。在此基础上只需要保证 \(f_i(x_i)=y_i\),也就是保证 \(\dfrac{f_i(x_i)}{y_i}=1\),可以选择在 \(x=x_i\) 时消去所有的 \(\prod_{j\neq i} (x-x_j)\),写成:
求和得到:
这样的复杂度是 \(O(n^2)\) 的。
取值连续拉格朗日插值
当出现 \(x_i=i\) 的特例时(事实上大部分都是这样的),正常的式子会更加简洁:
分子部分的 \(\prod_{j\neq i} (x-j)\) 可以前缀积后缀积预处理出 \(pre_i=\prod_{j=0}^{i-1} (x-j),suf_i=\prod_{j=i+1}^{n-1} (x-j)\)。
分母部分的 \(\prod_{j\neq i} (i-j)\),分正负讨论,\(i>j\) 时 \(\prod_{j=0}^{i-1} (i-j)=i!\),\(i<j\) 时提出负号 \((-1)^{n-1-i}\prod_{j=i+1}^{n-1} (j-i)=(-1)^{n-1-i} (n-1-i)!\)。
这样式子化简成:
这样的复杂度是 \(O(n)\) 的。
例题
Luogu-P4781 【模板】拉格朗日插值
点击查看代码
int n,k;
int X[maxn],Y[maxn];
inline int q_pow(int A,int B,int P){
A=(A%P+P)%P;
int res=1;
while(B){
if(B&1) res=1ll*res*A%P;
A=1ll*A*A%P;
B>>=1;
}
return res;
}
inline int Lagrange(int x){
int res=0;
for(int i=0;i<n;++i){
int now=Y[i];
for(int j=0;j<n;++j){
if(i==j) continue;
now=1ll*now*((x-X[j]+mod)%mod)%mod*q_pow(X[i]-X[j],mod-2,mod)%mod;
}
res=(res+now)%mod;
}
return res;
}
int main(){
n=read(),k=read();
for(int i=0;i<n;++i) X[i]=read(),Y[i]=read();
printf("%d\n",Lagrange(k));
return 0;
}
CodeForces-622F The Sum of the k-th Powers *2600
求自然数幂和 \(f(x)=\sum_{i=1}^x i^k\)。
由于 \(\Delta f(x)=x^k\) 为 \(k\) 次多项式,因此 \(f(x)\) 为 \(k+1\) 次多项式,从而需要 \(k+2\) 个点值插出多项式
LibreOJ-6024 XLkxc
定义以下函数:
因此 \(h(x)\) 的三阶差分是自然数幂,因此 \(h(x)\) 为 \(k+3\) 次多项式。
依次插出 \(f(x),g(x),h(x)\),所求即为 \(h(n)\)。
Luogu-P4463 集训队互测 2012 calc
若将所有选取集合相同的方案视为一种,设 \(f_{i,j}\) 为 前 \(i\) 个选取 \(j\) 个的方案,则有递推式:
则答案为 \(n!\times f_{k,n}\)。
将状态写成关于 \(i\) 的多项式,即 \(f_j(i)\),得到:
移项写成差分形式:
若 \(f_{j-1}(i)\) 是 \(m\) 次多项式,则等式右边是 \(m+1\) 次多项式,而差分前的 \(f_{j}(i)\) 是 \(m+2\) 次多项式。
考虑 \(j=0\) 的边界情况,此时 \(f_0(i)=1\),为 \(0\) 次多项式,因此 \(f_n(k)\) 应当为 \(2n\) 次多项式。只需要预处理出 \(2n+1\) 个点值即可。
快速傅里叶变换 FFT
用范德蒙德矩阵表示多项式求值
由于 \(n\) 个点唯一确定 \(n-1\) 次多项式,因此 \(m\) 中选择任意 \(n\) 个不同的 \(x_i\) 构成方阵,其方阵一定有逆。
而求出逆之后由点值计算系数就是多项式插值了。
离散傅里叶变换 DFT
离散傅里叶变换大多应用在工程当中,其实现了一个序列 \(x\) 到另一序列 \(X\) 的转换,并用到了多项式以及单位根,具体而言是:
即以 \(x\) 序列为系数构造出多项式并在每个单位根出求值。
接下来关于 FFT 的内容实际上是基于 DFT 的大致思想的。
对多点求值的优化
求 \(n\) 个点值显然是 \(O(n^2)\) 的。尝试降低这个复杂度,方式是 计算一次值可以被用于多个式子。
若所取的 \(x_i\) 均为形如 \((x_i,-x_i)\) 的相反数正对出现,则可以将计算次数减半,然而单次计算的复杂度仍然为 \(O(n)\)。
一个多项式函数一定可以看作一个奇函数与一个偶函数之和,即 \(f(x)=g(x)+h(x)\),其中 \(g(x)\) 为偶函数,\(h(x)\) 为奇函数。
将多项式按照奇偶拆分,则可以写成:
考虑到 \(g\) 的系数下标均为偶数,\(h\) 的系数下标均为奇数,如果枚举系数时直接枚举有贡献的下标就可以使得两个函数求值的总复杂度是 \(O(n)\)。
\(g'(x)\) 与 \(h'(x)\) 均为压缩后只剩下有效系数的多项式。
试想如果我们层层按照奇偶性一分为二,则只需要 \(w=\left\lceil\log n\right\rceil\) 层即可求出答案,为保证每一层的每个子问题都能被恰好一分为二,将 \(n\) 补全为 \(L=2^{w}\)。
接下来就要探究 \(L\) 个 \(x\) 该如何选择的问题了。
我们需要使得这 \(x\) 个数中相反数成对出现,再进行平方并去重之后相反数依旧成对出现,直至到最后一个值。
这时就需要使用单位根 \(\omega_L^k\),这恰好满足我们的需求。
递归
现在将单位根 \(\omega_L^k\ \left(k\in\left[0,\dfrac{L}{2}\right)\right)\) 代入上面的递归式子并且根据一些性质做化简:
递归常数过大,需要更优秀的写法。
蝴蝶变换
定义第 \(k\) 层递归为将规模为 \(\dfrac{L}{2^{k-1}}\) 的多项式分成两个规模为 \(\dfrac{L}{2^k}\) 的多项式进行计算。
那么系数 \(a_i\) 在第 \(1\) 层划分到 \(g'\) 或 \(h'\) 完全取决于 \(i\) 是偶数或奇数,而在第 \(k\) 层则是取决于 \(\left\lfloor\dfrac{i}{2^{k-1}}\right\rfloor\) 是偶数或奇数,抑或是 \(i\) 从低到高第 \(k\) 位是 \(0\) 或 \(1\)。
设 \(r_i\) 为 \(i\) 二进制翻转后的值,例如 \(11=(1011)_2,r_{11}=(1101)_2=13\)。
例如 \((a_0,a_1,\cdots,a_7)\) 在第一层分成 \((a_0,a_2,a_4,a_6),(a_1,a_3,a_5,a_7)\),第二次分成 \((a_0,a_4),(a_2,a_6),(a_1,a_3),(a_5,a_7)\),注意到此时下标的顺序已然是按照 \(r_i\) 排序的了,更具体地说,每个括号内的下标 \(r_i\) 都是连续的,于是我们可以将 \(i\) 的系数转移到 \(r_i\) 位置,每次向下递归都是将区间从中间一分为二,这才是最关键之处。
设当前处理的规模为 \(2d\),枚举 \(i=2kd\ (i\in[0,2d)),j\in[0,d)\)。目前的单位根应当为 \(\omega_{2d}\),而 \(\omega_{2d}^k=-\omega_{2d}^{k+d}\)。
注意到区间 \([i,i+2d)\) 应当划分为 \([i,i+d)\) 与 \([i+d,i+2d)\) 二者均在规模 \(d\) 时处理完成。而 \(i+j\) 与 \(i+d+j\) 位置的 \(2d\) 次单位根平方位置同样是 \(i+j\) 与 \(i+d+j\),且前者对应 \(g'\),后者对应 \(h'\)。
设 \(x=i+j,y=i+d+j\),则对应的点值序列 \(f'_x=f_x+\omega_{2d}^jf_y,f'_y=f_x-\omega_{2d}^jf_y\)。(此时 \(f_i\) 表示的是第 \(i\) 个 \(L\) 次单位根目前的点值。)
以上过程称作 快速傅里叶变换,我们注意到这实际上是快速求多个点值以确定多项式的 \(O(n\log n)\) 算法。
逆快速傅里叶变换 IFFT
上文最早提到的范德蒙德矩阵 \(\bm{F}\),本质是系数到点值的转换,也就是求值,而对矩阵的逆 \(\bm{F}^{-1}\),本质是点值到系数的转换,也就是插值。
在逆矩阵中,\(f(x_j)\) 对 \(a_i\) 的贡献是 \((\bm{F}^{-1})_{ij}\)。
将 \(x_i=\omega_{L}^i\) 代入拉格朗日插值的式子:
于是 \((\mathbf{F}^{-1})_{ij}=[x^i]\prod\limits_{k\neq j}\dfrac{x-\omega_{L}^k}{\omega_{L}^j-\omega_{L}^k}\)。
设 \(g_j(x)=\dfrac{\prod_{k=0}^{L-1} (x-\omega_{L}^k)}{x-\omega_{L}^j}\)。
分子部分实际上是 \(x^L-1\) 的展开(单位根的定义),于是 \(g_j(x)=\dfrac{x^L-1}{x-\omega_{L}^j}\)
使用短除法,发现:
代入到刚刚的表达式:
再回顾一下 FFT 构建的矩阵:
而刚刚计算出的逆矩阵:
因此只需要单位根取负次幂并最后除去系数即可。
快速多项式乘法
这才是 FFT 的最终目的。
\(n\) 次多项式 \(f(x)\) 与 \(m\) 次多项式 \(g(x)\) 的卷积 \(h(x)\) 为 \(n+m\) 次多项式。如果直接进行系数相乘求出 \(h\) 的话,复杂度是 \(O(nm)\) 的,然而 \(n+m\) 次多项式只需要 \(n+m+1\) 个点值,是线性的。
如果能以较快的速度将 \(f\) 与 \(g\) 的 \(n+m+1\) 个点值求出,乘积作为 \(h\) 的点值,再进而得到系数,那么复杂度将会很优秀。
也就是快速求值再快速插值,这个问题分别被 FFT 与 IFFT 解决了。
点击查看代码
int rev[maxn];
struct Complex{
db a,b;
Complex()=default;
Complex(db a_,db b_):a(a_),b(b_){}
Complex operator+(const Complex &rhs)const{return Complex(a+rhs.a,b+rhs.b);}
Complex operator-(const Complex &rhs)const{return Complex(a-rhs.a,b-rhs.b);}
Complex operator*(const Complex &rhs)const{return Complex(a*rhs.a-b*rhs.b,a*rhs.b+b*rhs.a);}
}base,W[maxn],w[maxn];
struct Poly{
int deg;
vector<Complex> f;
Complex &operator[](const int &i){return f[i];}
Complex operator[](const int &i)const{return f[i];}
inline void set(int L){deg=L;f.resize(L);}
inline void clear(int L,int R){for(int i=L;i<=R;++i)f[i]=Complex(0,0);}
inline void output(int L){for(int i=0;i<L;++i)printf("(%Lf,%Lf) ",f[i].a,f[i].b);printf("\n");}
inline void FFT(int L,bool type){
set(L);
for(int i=1;i<L;++i){
rev[i]=(rev[i>>1]>>1)+(i&1?L>>1:0);
if(i<rev[i]) swap(f[i],f[rev[i]]);
}
for(int d=1;d<L;d<<=1){
for(int i=0,j=0;i<d;++i,j+=L/(2*d)) w[i]=W[type?j:L-j];
for(int i=0;i<L;i+=d<<1){
for(int j=0;j<d;++j){
Complex x=f[i+j],y=w[j]*f[i+d+j];
f[i+j]=x+y,f[i+d+j]=x-y;
}
}
}
if(!type){
for(int i=0;i<L;++i) f[i].a/=L,f[i].b/=L;
}
}
};
多项式乘法计算出的系数实际上是两个系数序列的卷积,因此计算普通序列的卷积可以直接等价于序列看作多项式的系数,进行多项式乘法。
快速数论变换 NTT
实际上应当为 FNTT。
当我们的多项式定义在整数域且有模数质数 \(p=a\times 2^k+1\),可以使用 NTT 来代替 FFT 获得更高的精度,同时常数也更加小。
在 FFT 中我们使用了 \(L\) 次单位根 \(\omega_{L}\),由于 \(p\) 为质数一定有原根 \(g\),且 \(g\) 的 \([0,p-2]\) 次幂在模 \(p\) 下各不相同,这等价于单位根 \(\omega_{p-1}\) 的性质。
于是 \(\omega_{L}=\omega_{p-1}^{\frac{p-1}{L}}\),等价于 \(g^{\frac{p-1}{L}}\)。将其作为替换单位根 \(\omega_{L}\),即可得到在整数域的快速变换。
上面关于单位根与原根的转换,说明了我们对 \(p\) 的要求合理之处——\(L=2^w\mid p-1\),同时我们要求 \(k\ge w\)。
点击查看代码
inline int q_pow(int A,int B,int P){
int res=1;
while(B){
if(B&1) res=1ll*res*A%P;
A=1ll*A*A%P;
B>>=1;
}
return res;
}
int rev[maxn];
int base,w[maxn];
struct Poly{
const static int g=3;
int deg;
vector<ull> f;
ull &operator[](const int &i){return f[i];}
ull operator[](const int &i)const{return f[i];}
inline void set(int L){deg=L;f.resize(L);}
inline void clear(int L,int R){for(int i=L;i<=R;++i)f[i]=0;}
inline void output(int L){for(int i=0;i<L;++i)printf("%llu ",f[i]);printf("\n");}
inline void NTT(int L,bool type){
set(L);
for(int i=1;i<L;++i){
rev[i]=(rev[i>>1]>>1)+(i&1?L>>1:0);
if(i<rev[i]) swap(f[i],f[rev[i]]);
}
for(int d=1;d<L;d<<=1){
base=q_pow(type?g:q_pow(g,mod-2,mod),(mod-1)/(2*d),mod);
w[0]=1;
for(int i=1;i<d;++i) w[i]=1ll*w[i-1]*base%mod;
for(int i=0;i<L;i+=d<<1){
for(int j=0;j<d;++j){
ull x=f[i+j],y=f[i+d+j]*w[j]%mod;
f[i+j]=x+y,f[i+d+j]=x-y+mod;
}
}
}
for(int i=0;i<L;++i) f[i]%=mod;
if(!type){
int inv_L=q_pow(L,mod-2,mod);
for(int i=0;i<L;++i) f[i]=f[i]*inv_L%mod;
}
}
};
常见 NTT 模数有:
-
\(998244353=7\times 17\times 2^{23}+1\),原根 \(3\)。
-
\(1004535809=479\times 2^{21}+1\),原根 \(3\)。
-
\(469762049=7\times 2^{26}+1\),原根 \(3\)。
应用
差卷积
对于长度均为 \(n\) 的序列 \(f\) 与 \(g\),上面已经提到卷积可以看做是多项式乘法的系数。
和卷积的形式为:
进行操作为对 \(f,g\) 分别做一次 FFT,再乘出 \(h\) 的点值并对 \(h\) 做 IFFT,即得 \(h\) 系数。
而差卷积的形式为:
解法 \(1\)
比较常规,将 \(g\) 翻转,即令 \(g'_i=g_{n-i}\),这样等式右边为:
于是按照和卷积运算,答案的位置是 \(h_{n+k}\)。
解法 \(2\)
尝试直接令 \(g'_i=g_{-i}\),再回到多项式乘法与序列卷积的关系中,就相当于变成了:
如果在上式代入 \(x_i^{-1}\) 作为点值 \((x_i,y_i)\),那么消去负号后同正常的多项式没有区别。
因此代入单位根时修改为 \(\omega_{2d}^{-k}\) 即可。
分治 FFT
考虑形如:
的半在线卷积,求出 \(n\) 需要在已知 \(0\sim n-1\) 的情况下,此时可以使用 CDQ 分治。
设当前区间 \([l,r]\),先向下处理 \([l,mid]\),此时 \(0\sim mid\) 处的值完全已知。考虑 \([l,mid]\) 对 \([mid+1,r]\) 的贡献,实际上就是与 \(g\) 卷积。由于 \(f\) 有贡献的部分为左区间大小,\(g\) 有贡献的部分为整个区间大小,所以在一层分治中,总复杂度为 \(n\) 次多项式的卷积复杂度,\(\log n\) 层的总复杂度即为 \(O(n\log^2n)\)。
具体地说,在卷积时令 \(f'_i=f_{l+i}\),与 \(g\) 的卷积结果 \(h_i\) 贡献到 \(f_{l+i}\) 处。
点击查看代码
inline int q_pow(int A,int B,int P){
int res=1;
while(B){
if(B&1) res=1ll*res*A%P;
A=1ll*A*A%P;
B>>=1;
}
return res;
}
int rev[maxn];
int base,w[maxn];
struct Poly{
const static int g=3;
int deg;
vector<ull> f;
ull &operator[](const int &i){return f[i];}
ull operator[](const int &i)const{return f[i];}
inline void set(int L){deg=L;f.resize(L);}
inline void clear(int L,int R){for(int i=L;i<=R;++i)f[i]=0;}
inline void output(int L){for(int i=0;i<L;++i)printf("%llu ",f[i]);printf("\n");}
inline void NTT(int L,bool type){
set(L);
for(int i=1;i<L;++i){
rev[i]=(rev[i>>1]>>1)+(i&1?L>>1:0);
if(i<rev[i]) swap(f[i],f[rev[i]]);
}
for(int d=1;d<L;d<<=1){
base=q_pow(type?g:q_pow(g,mod-2,mod),(mod-1)/(2*d),mod);
w[0]=1;
for(int i=1;i<d;++i) w[i]=1ll*w[i-1]*base%mod;
for(int i=0;i<L;i+=d<<1){
for(int j=0;j<d;++j){
ull x=f[i+j],y=f[i+d+j]*w[j]%mod;
f[i+j]=x+y,f[i+d+j]=x-y+mod;
}
}
}
for(int i=0;i<L;++i) f[i]%=mod;
if(!type){
int inv_L=q_pow(L,mod-2,mod);
for(int i=0;i<L;++i) f[i]=f[i]*inv_L%mod;
}
}
}F,G,H;
int f[maxn],g[maxn];
#define mid ((l+r)>>1)
#define siz (r-l+1)
inline void Conquer(int l,int r){
if(l==r) return;
Conquer(l,mid);
int L=1;
while(L<2*siz) L<<=1;
F.set(L),G.set(L),H.set(L);
F.clear(0,L-1),G.clear(0,L-1);
for(int i=l;i<=mid;++i) F[i-l]=f[i];
for(int i=l;i<=r;++i) G[i-l]=g[i-l];
F.NTT(L,1),G.NTT(L,1);
for(int i=0;i<L;++i) H[i]=F[i]*G[i]%mod;
H.NTT(L,0);
for(int i=mid+1;i<=r;++i) f[i]=(f[i]+H[i-l])%mod;
Conquer(mid+1,r);
}
#undef mid
#undef siz


 浙公网安备 33010602011771号
浙公网安备 33010602011771号