【学习笔记】图的连通性
无向图连通性
一些定义
若无向图 \(G\) 中任意不同两点 \((u,v)\) 都有路径可达,称 \(G\) 为一个 连通图,若 \(G\) 的一个子集 \(H\) 满足不存在连通子图 \(G'\) 满足 \(H\subseteq G'\),则 \(H\) 为一个 连通块/连通分量,也即极大连通子图。
若无向图 \(G\) 中存在一个点集 \(V'\) 满足删去这些点以及连边后,原图的连通分量个数会增加,称点集 \(V'\) 为一个 点割集,特别地,当 \(V'\) 中只含一个节点 \(u\) 时,称节点 \(u\) 为 割点。
若无向图 \(G\) 中存在一个边集 \(E'\) 满足删去这些边后,原图的连通分量个数会增加,称边集 \(E'\) 为一个 边割集,特别地,当 \(E'\) 中只含一条边 \((u,v)\) 时,称边 \((u,v)\) 为 割边/桥。
若一个连通图中不含割点,则该连通图 点双连通;若一个连通图中不含割边,则该连通图 边双连通。类比连通分量的定义,同样有 点双连通分量 与 边双连通分量。
割点
使用 Tarjan 算法。
在无向图 DFS 树中,横叉边是不存在的,因此每个 \(u\) 的每个儿子 \(v_i\) 的子树 \(T(v_i)\) 都是两两独立的,这个性质在后续会不断用到。
割点不为 DFS 树根时
对非树根 \(u\) 讨论,其作为割点的充要条件是删去 \(u\) 后存在一棵子树 \(T(v_i)\) 成为连通块,也就是存在一棵子树 \(T(v_i)\),其内部的任意节点是无法在不经过 \(u\) 的前提下去到子树外。
思考可以不经过 \(u\) 去到子树外的一颗子树 \(T(v_i)\),这条路径应当是若干 \(T(v_i)\) 内部的边与一条返祖边 \((w,f)\) 组成,由于 DFS 树中不含横叉边,则 \(f\) 应当是 \(u\) 的一个祖先,于是 \(\mathrm{dfn}(f)<\mathrm{dfn}(u)\)。
因此只需要维护 \(\mathrm{low}(v_i)\) 表示子树 \(T(v_i)\) 内所有节点中 只通过一条非树边 可以去到的最小 \(\mathrm{dfn}\) 值。
关于“只经过一条非树边”的设定
这样的设定足以满足我们对割点的探究,思考为什么更广泛的定义会出现错误。
原因在于一个割点可能对应多个点双连通分量,因此存在一个节点先后通过两条非树边到达割点再走到割点的祖先,此时就违背了刚才“不经过 \(u\)”的前提。
\(\mathrm{low}(u)\) 的计算方法如下:
-
初始设置为 \(\mathrm{dfn}(u)\)
-
当 \(v\) 未被访问时,是一条树边,更新 \(\mathrm{low}(u)=\min(\mathrm{low}(u),\mathrm{low}(v))\)
-
当 \(v\) 已被访问时,是一条返祖边或前向边,后者对答案无影响,根据对 \(\mathrm{low}(u)\) 的定义,更新 \(\mathrm{low}(u)=\min(\mathrm{low}(u),\mathrm{dfn}(v))\)。
于是当 \(u\) 存在一个子树 \(T(v_i)\) 满足 \(\mathrm{low}(v_i)\ge \mathrm{dfn}(u)\),说明 \(u\) 是割点。
割点为 DFS 树根时
容易发现,当树根出现不只一棵子树时,两棵子树间唯一路径为经过根的路径,即此时根是割点。
点击查看代码
struct Graph{
vector<int> E[maxn];
inline void add_edge(int u,int v){
E[u].push_back(v);
E[v].push_back(u);
}
int rt;
int dfn[maxn],low[maxn],dfncnt;
bool vcut[maxn];
int cnt_vcut;
void Tarjan(int u){
dfn[u]=++dfncnt,low[u]=dfn[u];
int cnt_son=0;
for(int v:E[u]){
if(!dfn[v]){
++cnt_son;
Tarjan(v);
low[u]=min(low[u],low[v]);
if(u!=rt&&low[v]>=dfn[u]) vcut[u]=1;
}
else{
low[u]=min(low[u],dfn[v]);
}
}
if(u==rt&&cnt_son>1) vcut[u]=1;
if(vcut[u]) ++cnt_vcut;
}
inline void solve(){
for(int u=1;u<=n;++u){
if(!dfn[u]){
rt=u;
Tarjan(u);
}
}
printf("%d\n",cnt_vcut);
for(int u=1;u<=n;++u){
if(vcut[u]) printf("%d ",u);
}
printf("\n");
}
}G;
割边
割边一定是 DFS 树的非树边,在割点的基础上修改算法流程,注意到 \(T(v_i)\) 可以经过非树边返回 \(u\) 则 \((u,v_i)\) 并不属于割边,因此判断条件修改为:\(\mathrm{low}(v_i)>\mathrm{dfn}(u)\)。
且求割边不需要讨论根的问题。
有重边时用邻接表存图,\(cnt\) 从 \(2\) 开始记录,这样正反两条边的编号是异或关系,判断是不是同一条边即可。
点击查看代码
struct Graph{
struct edge{
int to,nxt;
}e[maxm<<1];
int head[maxn],cnt;
Graph(){
cnt=1;
}
inline void add_edge(int u,int v){
e[++cnt].to=v,e[cnt].nxt=head[u],head[u]=cnt;
e[++cnt].to=u,e[cnt].nxt=head[v],head[v]=cnt;
}
int fa[maxn];
int dfn[maxn],low[maxn],dfncnt;
bool ecut[maxn];
int cnt_ecut;
void Tarjan(int u,int f,int id){
dfn[u]=++dfncnt,low[u]=dfn[u];
for(int i=head[u];i;i=e[i].nxt){
if(i==id) continue;
int v=e[i].to;
if(!dfn[v]){
Tarjan(v,u,i^1);
low[u]=min(low[u],low[v]);
if(low[v]>dfn[u]) ecut[v]=1;
}
else{
low[u]=min(low[u],dfn[v]);
}
}
}
inline void solve(){
for(int u=1;u<=n;++u){
if(!dfn[u]){
Tarjan(u,0,0);
}
}
for(int u=1;u<=n;++u){
if(ecut[u]) ++cnt_ecut;
}
printf("%d\n",cnt_ecut);
for(int u=1;u<=n;++u){
if(ecut[u]) printf("%d %d\n",u,fa[u]);
}
}
}G;
边双连通分量
考虑一个简单粗暴的做法,先 Tarjan 求出所有割边之后暴力 DFS,但是很不优美。
我们使用一个同时求出割边并缩点的做法,具体利用一个栈,这个方法将在各种缩点中一直用到。
在访问到一个节点时将其加入栈,当 \((u,v)\) 为割边时(此时 \(v\) 内遍历完回溯至 \(u\)),设将其分成了 \(G_u,G_v\) 两个子图,考虑到子树间独立,\(G_v\) 内部的点都在 \(v\) 之前入栈,而在 \(G_v\) 内部其他边双连通分量都已经被从栈求出(设另一割边 \((x,y)\),则 \(y\) 遍历完回溯 \(x\) 一定在这之前),因此栈中 \(v\) 到栈顶的节点都属于 \(v\) 的边双连通分量。
于是暴力弹栈即可。
点击查看代码
struct Graph{
struct edge{
int to,nxt;
}e[maxm<<1];
int head[maxn],cnt;
Graph(){
cnt=1;
}
inline void add_edge(int u,int v){
e[++cnt].to=v,e[cnt].nxt=head[u],head[u]=cnt;
e[++cnt].to=u,e[cnt].nxt=head[v],head[v]=cnt;
}
int dfn[maxn],low[maxn],dfncnt;
int st[maxn],top;
int ebcc[maxn],cnt_ebcc;
vector<int> EBCC[maxn];
void Tarjan(int u,int id){
dfn[u]=++dfncnt,low[u]=dfn[u];
st[++top]=u;
for(int i=head[u];i;i=e[i].nxt){
if(i==id) continue;
int v=e[i].to;
if(!dfn[v]){
Tarjan(v,i^1);
low[u]=min(low[u],low[v]);
if(low[v]>dfn[u]){
++cnt_ebcc;
while(st[top]!=v){
ebcc[st[top]]=cnt_ebcc;
EBCC[cnt_ebcc].push_back(st[top]);
--top;
}
ebcc[v]=cnt_ebcc;
EBCC[cnt_ebcc].push_back(v);
--top;
}
}
else{
low[u]=min(low[u],dfn[v]);
}
}
}
inline void solve(){
for(int u=1;u<=n;++u){
if(!dfn[u]){
Tarjan(u,0);
++cnt_ebcc;
while(top){
ebcc[st[top]]=cnt_ebcc;
EBCC[cnt_ebcc].push_back(st[top]);
--top;
}
}
}
printf("%d\n",cnt_ebcc);
for(int i=1;i<=cnt_ebcc;++i){
printf("%ld ",EBCC[i].size());
for(int u:EBCC[i]){
printf("%d ",u);
}
printf("\n");
}
}
}G;
点双连通分量
与边双连通分量类似,在 \(u\) 为割点时弹栈,要注意以下四点:
-
弹栈时栈顶到 \(v\) 都属于这个点双连通分量,同时割点 \(u\) 也属于这个点双连通分量但不一定在栈中与 \(v\) 相邻。
-
\(u\) 可能在多个点双连通分量中,不能弹栈;但 \(v\) 的子树内所有点双连通分量都已经处理,可以弹栈。
-
每次 DFS 后的栈中剩余一个元素是 DFS 树的根。
-
孤立点也是一个点双连通分量。
点击查看代码
struct Graph{
vector<int> E[maxn];
inline void add_edge(int u,int v){
E[u].push_back(v);
E[v].push_back(u);
}
int dfn[maxn],low[maxn],dfncnt;
int st[maxn],top;
int cnt_vbcc;
bool vbcc[maxn];
vector<int> VBCC[maxn];
void Tarjan(int u){
dfn[u]=++dfncnt,low[u]=dfn[u];
st[++top]=u;
for(int v:E[u]){
if(!dfn[v]){
Tarjan(v);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]){
++cnt_vbcc;
while(st[top]!=v){
vbcc[st[top]]=1;
VBCC[cnt_vbcc].push_back(st[top]);
--top;
}
vbcc[v]=1;
VBCC[cnt_vbcc].push_back(v);
--top;
vbcc[u]=1;
VBCC[cnt_vbcc].push_back(u);
}
}
else{
low[u]=min(low[u],dfn[v]);
}
}
}
inline void solve(){
for(int u=1;u<=n;++u){
if(!dfn[u]){
Tarjan(u);
if(!vbcc[u]){
++cnt_vbcc;
VBCC[cnt_vbcc].push_back(st[top]);
}
--top;
}
}
printf("%d\n",cnt_vbcc);
for(int i=1;i<=cnt_vbcc;++i){
printf("%ld ",VBCC[i].size());
for(int u:VBCC[i]){
printf("%d ",u);
}
printf("\n");
}
}
}G;
然而点双连通分量的“缩点”是有矛盾的(一个点出现在多个点双连通分量中),我们想要达成的效果实际上是“缩边”,这一点会在下文的圆方树中提到。
有向图连通性
一些定义
若有向图 \(G\) 中任意不同两点 \((u,v)\) 都有路径可达,称 \(G\) 为一个 强连通图,若 \(G\) 的一个子集 \(H\) 满足不存在连通子图 \(G'\) 满足 \(H\subseteq G'\),则 \(H\) 为一个 强连通分量。
若将有向图 \(G\) 中所有有向边替换成无向边后 \(G'\) 是一无向连通图,则称 \(G\) 为一个 弱连通图,同样也有 弱联通分量 的定义。
若有向图 \(G\) 中所有无序点对 \((u,v)\) 至少满足 \(u\) 可达 \(v\) 或 \(v\) 可达 \(u\),则称 \(G\) 为一个 单向连通图。
强连通分量
下面的介绍将类比无向图中边双连通分量缩点的算法流程。
有向图 DFS 的子树虽然不保证完全独立,依然满足所有的横叉边 \((u,v)\) 都有 \(\mathrm{dfn}(u)>\mathrm{dfn}(v)\),这一性质会广泛用到。
下面来讨论三种非树边对连通性的影响:
-
前向边:没有任何影响,等价于树上路径。
-
返祖边:边的两端点之间形成一个简单的强连通分量,同时可以与其他强连通分量结合。
-
横叉边:可以到达时间戳更小的节点。
也就说有必要好好研究的就是横叉边,给出一个性质:若存在横叉边 \((u,v)\) 则 \(v\) 可达 \(u\) 当且仅当 \(v\) 可达 \(\mathrm{LCA}(u,v)\)。
充分性显然。
必要性考虑如何在不经过 \(\mathrm{LCA}(u,v)\) 的情况下到达 \(u\),此时返祖边结合树边是无用的,似乎只能借助与横叉边,而显然横叉边 \((u,v)\) 的存在就代表着 \(u\) 所在子树的时间戳都大于 \(v\) 所在子树,且横叉边只能从较大时间戳到较小时间戳,因此横叉边也无法使用,于是得证。
若 \(u,v\) 同时存在一个强连通分量里,则这个强连通分量树上深度最小的点至少是 \(\mathrm{LCA}(u,v)\),因此一个强连通分量深度最小的点只有一个。我们希望在这个点记录强连通分量。
一个点如果不是强连通分量中深度最小的点,则一定可以通过一系列的横叉边以及返祖边去到自己的祖先位置,而这个祖先位置就是强连通分量中最小的点。
于是我们继续定义 \(\mathrm{low}(u)\) 为 \(u\) 通过非树边可以去到的最小时间戳。
下面是更新 \(\mathrm{low}(u)\) 的方式:
-
初始设置为 \(\mathrm{dfn}(u)\)
-
当 \(v\) 未被访问时,是一条树边,更新 \(\mathrm{low}(u)=\min(\mathrm{low}(u),\mathrm{low}(v))\)
-
当 \(v\) 已被访问时且已经弹栈,不再更新
-
当 \(v\) 已经被访问且未弹栈,更新 \(\mathrm{low}(u)=\min(\mathrm{low}(u),\mathrm{dfn}(v))\)
关于已经弹栈后不更新
\(v\) 已经弹栈说明 \(v\) 不可达 \(\mathrm{LCA}(u,v)\)(当前还处于 \(\mathrm{LCA}(u,v)\) 子树中,已经弹栈说明不在统一强连通分量),于是到达 \(v\) 对 \(u\) 的连通性是没有意义的。
这样当 \(\mathrm{dfn}(u)=\mathrm{low}(u)\) 时,说明 \(u\) 是当前强连通分量的最小深度节点,类比上文边双连通分量的证明,此时栈顶到 \(u\) 的所有节点都属于该强连通分量。
关于未弹栈时更新的转移
这里写作 \(\mathrm{dfn}(v)\) 或 \(\mathrm{low}(v)\) 均可,不同与割点割边时对一次非树边的限制,这里更新主要目的是检验 \(u\) 是否是最小深度节点,只需要让 \(\mathrm{low}(u)<\mathrm{dfn}(u)\) 就可以。
点击查看代码
struct Graph{
vector<int> E[maxn];
inline void add_edge(int u,int v){
E[u].push_back(v);
E[v].push_back(u);
}
int dfn[maxn],low[maxn],dfncnt;
int st[maxn],top;
int scc[maxn],cnt_scc;
vector<int> SCC[maxn];
void Tarjan(int u){
dfn[u]=++dfncnt,low[u]=dfncnt;
st[++top]=u;
for(int v:E[u]){
if(!dfn[v]){
Tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(!scc[v]){
low[u]=min(low[u],dfn[v]);// or low[u]=min(low[u],low[v])
}
}
if(dfn[u]==low[u]){
++cnt_scc;
while(st[top]!=u){
scc[st[top]]=cnt_scc;
SCC[cnt_scc].push_back(st[top]);
--top;
}
scc[u]=cnt_scc;
SCC[cnt_scc].push_back(u);
--top;
}
}
inline void solve(){
for(int u=1;u<=n;++u){
if(!dfn[u]) Tarjan(u);
}
}
}G;
圆方树
构建
狭义圆方树处理仙人掌(每条边最多只出现在一个简单环中),将环视作方点,点视作圆点;广义圆方树处理点双连通分量的缩点,将点双视作方点,点视作圆点。环是点双的简单情况,因此本部分讲解广义圆方树。
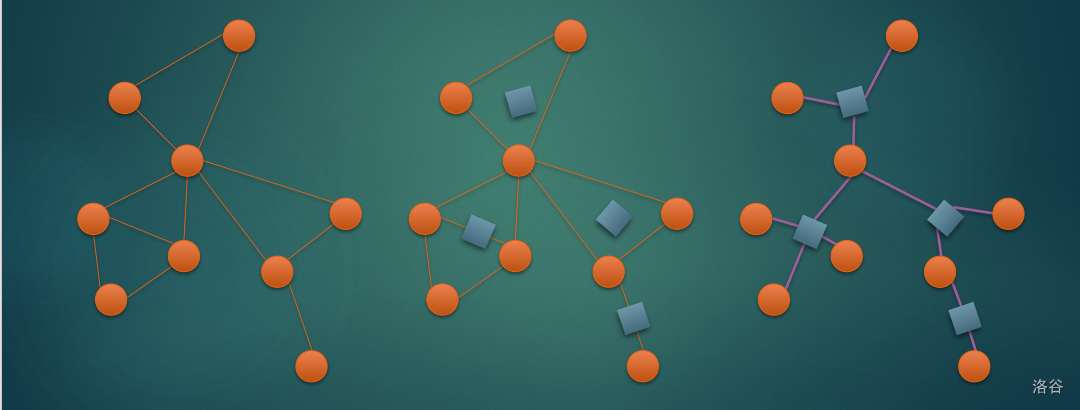
容易发现一条边两端点应为一圆一方,且两个点双最多只有一个公共点(割点),因此形成一棵树。
圆方树的构建实际上就是求点双的过程。
点击查看代码
struct Graph{
vector<int> E[maxn];
inline void add_edge(int u,int v){
E[u].push_back(v);
E[v].push_back(u);
}
int dfn[maxn],low[maxn],dfncnt;
int st[maxn],top;
void Tarjan(int u){
dfn[u]=++dfncnt,low[u]=dfn[u];
st[++top]=u;
for(int v:E[u]){
if(!dfn[v]){
Tarjan(v);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]){
++tot;
while(st[top]!=v){
T.add_edge(tot,st[top]);
--top;
}
T.add_edge(tot,v);
--top;
T.add_edge(tot,u);
}
}
else{
low[u]=min(low[u],dfn[v]);
}
}
}
inline void solve(){
tot=n;
Tarjan(1);
}
}G;
例题
Luogu-P4630 APIO 2018 铁人两项
建出圆方树,考虑在 \((u,v,w)\) 的中间点 \(v\) 处统计答案。
一个样例(加粗为方点):
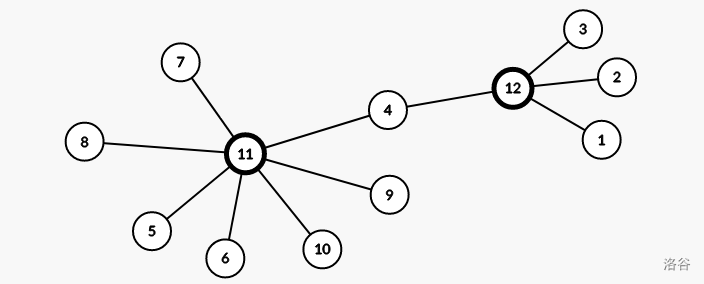
先不考虑点双的影响,圆点 \(v\) 不同子树内的节点可以构成简单的 \((u,v,w)\),例如路径 \((2,4,5)\),此类只需要记录子树大小 \(sum\) 即可。
点双内部任意选三个点都可以构成答案,即 \(siz\times (siz-1)\times (siz-2)\),例如路径 \((1,2,3)\)。
最后一步是考虑点双的作用,刚刚在圆点处统计答案中 \(u,w\) 来自不同的子树,而借助点双,可以在圆点的同一个子树中得到一条路径,例如路径 \((1,7,8)\) 是圆点 \(7\) 同一子树中的,但他们来自方点 \(11\) 的不同子树。
考虑子树 \(u\) 与 \(w\),枚举圆点 \(v\),在方点处记录答案。其中 \(v\) 应当与 \(u,w\) 子树的根不同,因此有 \(siz-2\) 种方案,而 \(u,w\) 子树同时选择根时等价于前面计算的点双内部,需要去除,因此考虑方点两棵子树的答案是:
可以把 \(-1\) 拆出来在最后统一计算。
Luogu-P4606 SDOI 2018 战略游戏
删去的点一定是割点,建出圆方树,每次把选中的节点的虚树建出,虚树中非选中的圆点个数即为答案。
CodeForces-487E Tourists *3200
能够想出圆方树+树链剖分,并用 multiset 维护方点对应的所有圆点最小值。
暴力修改一个圆点对应的所有方点肯定是不行的,考虑对于每个方点只维护其所有儿子的最小值,这样每次修改圆点只需要修改父亲。而当方点不是路径 \(\mathrm{LCA}\) 时,其父亲本身已经被统计过了,反之额外统计一下父亲的贡献。
Luogu-P4334 COI 2007 Policija
本意是求给定的点/边是否是给定路径的割点/边。
比较无脑的做法是分别建出点双的圆方树和边双缩点后的树。
对于查询点的操作,只需要判断该点是否在给定路径上即可;对于查询边的操作,排除点对在同一边双的情况后,判断该边(也就是两个点)是否在给定路径上。
后者的操作也可以在圆方树上进行,是割边的充要条件为二者共同的点双大小为 \(2\),这也保证了该方点至于这两个圆点相连,于是再判断方点是否再给定路径上。
参考资料
无向图连通性
有向图连通性
圆方树
-
OI Wiki


 浙公网安备 33010602011771号
浙公网安备 33010602011771号