Some Conclusions.

目录

• DP
  • 四边形不等式
• 数论 & 数学
• 数据结构
  • 树链剖分
  • 左偏树的性质及\(O(n)\)的构造
• 图论
  • 树
  • 二分图
  • 竞赛图
  • 平面图
  • 双连通分量
• 位运算
• 字符串
  • 后缀自动机
• 复杂度分析

---

没什么好写的。。（懒得补）

一些博客：http://www.cnblogs.com/GuessYCB/p/9090878.html
http://www.cnblogs.com/fenghaoran/p/remember.html

DP

四边形不等式

参考
一般对于如下形式状态转移方程：\(f[i][j]=\min\ or\ \max(f[i][k-1],f[k][j])+cost[i][j]\)，\(i<j\)且\(i<k\leq j\)。
1. 四边形不等式
　　若一个函数\(cost[i][j]\)，满足 \(cost[i][j]+cost[i'][j']\leq cost[i][j']+cost[i'][j]\)，其中 \(i\leq i'<j\leq j'\)，则称\(cost\)满足凸四边形不等式。(可理解为两交错区间之和不超过大区间与小区间之和)

2. 区间包含的单调性
　　若一个函数\(cost[i][j]\)，满足 \(cost[i'][j]\leq cost[i][j']\)，其中 \(i\leq i'<j\leq j'\)，则称\(cost\)关于区间包含关系单调。(可理解为被包含的小区间\(cost\)之和不超过大区间)

3. 定理一
　　若\(cost\)同时满足四边形不等式和区间单调关系，则 \(f\) 也满足四边形不等式。

4. 定理二(关键)
　　若 \(f\) 满足四边形不等式，则决策单调，即 \(P[i][j-1]\leq P[i][j]\leq P[i+1][j]\) 或 \(P[i-1][j]\leq P[i][j]\leq P[i][j+1]\) 等，此处可据需要表示，只要 \(P\) 符合单调即可。据此可以缩小决策枚举区间，进行优化。

5. 定理三
　　\(cost\)为凸当且仅当 \(cost[i][j]+cost[i+1][j+1]\leq cost[i+1][j]+cost[i][j+1]\)。
　　据此可以简单验证cost是否满足凸四边形不等式，将 \(i'\) 具体为 \(i+1\)，\(j'\) 具体为 \(j+1\)，然后对式子变形，再固定一个变量，看做一个一元函数，进而判断单调性。如可变形为 \(cost[i+1][j+1]-cost[i+1][j]\leq cost[i][j+1]-cost[i][j]\)，固定 \(j\)，看 \(cost[i][j+1]-cost[i][j]\) 是关于 \(i\) 递增还是递减，若是递增，则cost为凸。
　　实际中大多只需打表观察cost是否满足四边形不等式、是否单调即可。具体可以见上面的链接。。（懒得再写）

数论 & 数学

见这儿。

数据结构

树链剖分

1. 如果边 u->v 为轻边，那么 \(size[v]\leq size[u]/2\)。

证明：若 \(size[v]>size[u]/2\)，那么 u->v 会成为一条重边。

2. 树中任意两个节点之间的路径中重链、轻边的条数均不会超过\(log_2n\)，即树上任意一条链由不超过\(log_2n\)条重链和轻边组成。

证明：从根到任意非根节点 每遇到一条轻边，size至少会减半。

左偏树的性质及\(O(n)\)的构造

粘个链接。
性质一：节点的权值小于等于它左右儿子的权值。
性质二：节点的左儿子的距离不小于右儿子的距离。
在写平衡树的时候，我们是确保它的深度尽量的小，这样访问每个节点都很快。但是左偏树不需要这样，它的目的是快速提取最小节点和快速合并。所以它并不平衡，而且向左偏。但是距离和深度不一样，左偏树并不意味着左子树的节点数或是深度一定大于右子树。
性质三：节点的距离等于右儿子的距离+1。
性质四：一个n个节点的左偏树距离最大为log(n+1)−1

图论

树

重心 直径的性质（参考：这里和这里，以及平时做的一些题）

1. （定义）删去重心后的树尽可能平衡，即以重心为根，所有子树大小都不超过整棵树的一半。
2. 树中所有点到某个点的距离和中，到重心的距离和是最小的，如果有两个重心，他们的距离和一样。例：BZOJ3510 首都.

Proof: 如果不是重心，那么向重心走一步，由求重心的过程可以知道答案一定会变小。

3. 把两棵树通过某一点相连得到一颗新的树，新的树的重心必然在连接原来两棵树重心的路径上。
4. 一棵树添加或者删除一个节点，树的重心最多只移动一条边的位置。
5. 树的中心一定在直径的中点上。树的中心是到最远点的距离最小的点。
6. 从树上任意一个点 \(dfs\)，所到达的所有最远的点都是直径的端点。

Proof：如果该点是直径端点则显然，否则假设两个点是\(PQ\)，分类讨论与直径\(AB\)是否有交点。
无论与直径是否有交点，总能证明 原直径的一部分边+PQ的一部分边，长度大于原直径。

7. 树的所有直径必交于某一点或某条边。

二分图

1. 若一个图不存在奇环，那么这是二分图；如果含有奇一定不是二分图。（二分图中的环只能是偶环，无奇环）

竞赛图

Defination：每对顶点之间都有一条(有向)边相连的有向图。
性质：（证明见这）
1. 竞赛图一定存在哈密顿通路，强连通竞赛图一定存在哈密顿回路（强连通为其充要条件）。
2. \((n\geq 3\ ,3\leq i\leq n)\) n个点的强连通竞赛图中包含有长度为i的简单环。
3. 竞赛图缩点后一定是条链。

平面图

Defination：若能将无向图G=(V,E)画在平面上使得任意两条无重合顶点的边不相交，则称G是平面图。
link: 可平面图--百度百科
性质：平面图的边数 \(m\leq3*n-6\).
应用：在平面图中将边数降到\(O(n)\)级别，如BZOJ1997（如果边数大于\(3n-6\)则不是平面图）.

双连通分量

Point(Edge) Biconnected Component)
Defination：双连通分量分双连通分量和边双连通分量两种。若一个无向图中的去掉任意一个节点（一条边）都不会改变此图的连通性，即不存在割点（桥），则称作点（边）双连通图。
link: 双连通分量--百度百科
性质1：如果一个双连通分量内的某些顶点在一个奇圈中(即双连通分量含有奇圈)，那么这个双连通分量的其他顶点也在某个奇圈中；
性质2：如果一个双连通分量含有奇圈，则他必定不是一个二分图。反过来也成立，这是一个充要条件。

位运算

1. a^b + ((a&b)<<1) = a+b

字符串

后缀自动机

　　https://www.cnblogs.com/SovietPower/p/9118563.html。

复杂度分析

1.
大\(O\)：

　　我们用记号\(O(n)\)表示一个量时（这个量关于\(n\)的阶不超过\(n\)的阶），它本身是否真的包含阶为\(n\)的项，都是不确定的。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　——巴赫曼

公式

\[f(n)=O(g(n))，对所有n成立 \tag{1} \]

表示存在一个常数\(C\)，使得

\[|f(n)|\leq C|g(n)|，对所有n成立 \tag{2} \]

大\(\Omega\)：
大\(O\)给出了函数增长的上界，而下界有另外的一个记号，即大\(\Omega\)。

\[f(n)=\Omega(g(n))\Leftrightarrow|f(n)|\geq C|g(n)|\ \ \ \ 对某个C>0 \tag{3} \]

大\(\mathcal O\)（或\(\Theta\)）：
大\(\mathcal O\)指出精确的增长的阶：

\[f(n)=\mathcal O(g(n))\Leftrightarrow f(n)=O(g(n))且f(n)=\Omega(g(n)) \tag{4} \]

小\(o\)：
爱德蒙·兰道曾创立过一个“小\(o\)”记号，

\[f(n)=o(g(n))\Leftrightarrow|f(n)|\leq\varepsilon|g(n)|\ \ \ \ 所有n\geq n_0(\varepsilon)以及所有常数\varepsilon>0 \tag{5} \]

这个更全更直观。

2. 均摊\(\leq\)严格\(<\)期望
　　(非持久化下)均摊 \(O(n)=\) 严格 \(O(n)\)。
　　期望 \(O(n)\) 仅在数据随机情况下 \(O(n)\)，但是好像很难卡掉？

3. 启发式合并的总复杂度为 \(O(n\log n)\)，因为每个点最多被合并 \(O(\log n)\) 次。
　　每个点被从小集合合并到大的集合中时，它的集合大小会翻倍。
　　支持finger search的数据结构启发式合并都是一个\(\log\)的，比如splay。

4. 复杂度均摊的数据结构不能实现可持久化。

5. LCT的本质是用Splay维护链剖分。LCT不用别的平衡树维护是因为Splay均摊分析下是\(O(\log n)\)，其它平衡树是\(O(\log^2n)\)。

6. 形如这样的树形DP的复杂度：

void DFS(int x,int fa)
...
DFS(v=son[x],x);

for(int i=0; i<=size[x]; ++i)
	for(int j=0; j<=size[v]; ++j)
		tmp[i+j]=f[x][i]*f[v][j];
size[x]+=size[v];
...

复杂度是\(O(n^2)\)的。可以理解为每个点对只会在LCA处被统计一次，也可以归纳：
\(T(a+b)=T(a)+T(b)+ab\\\frac{(a+b)^2}{2}=\frac{a^2}{2}+\frac{b^2}{2}+ab\)
所以\(T(n)=\frac{n^2}{2}\)
或者：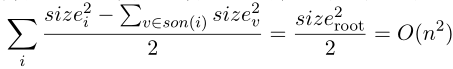

7. 个人对线段树合并复杂度的感性证明...

每次合并两棵树，代价是两棵树的公共节点数，设它是\(x\)。
在合并完两棵树后，这两棵树的\(2*x\)个公共节点被合并成了\(x\)个，相当于删掉了\(x\)个点。
所以合并的代价（复杂度）就是，被合并点的点的个数，也就是删掉的点的个数。
而要删掉这个点就要先存在这个点，初始一共有\(n\log n\)个节点，所以删掉点的个数不会超过\(n\log n\)，所以总复杂度不会超过\(n\log n\)。

如果初始是对每个节点进行一次区间修改，和插入单点一样只会影响\(\log n\)个点，所以初始还是一共最多有\(n\log n\)个点。

另外复杂度也不完全是公共节点数，因为还要从它往下一层才知道它是公共节点。
也许是这个能卡些线段树合并的复杂度吧，但是影响不大不管了。

8. \(\frac{2^{2n}}{C_{2n}^n}=O(\sqrt n)\)

9. \(O(\log n!)=O(n\log n)\)