AGC 019F.Yes or No(思路 组合)

题目链接

\(Description\)

一共有\(n+m\)道判断题，其中有\(n\)个答案为"YES"，\(m\)个为"NO"。现在以随机顺序给你这\(n+m\)道题，你需要依次回答，每回答一道题就会告诉你该题的正确答案。求最优策略下期望答对多少题。
\(n,m\leq 5\times10^5\)。

\(Solution\)

最优策略自然是每次答剩下数目多的。
每次回答问题要么答对要么答错，且使对应题数-1，不妨用坐标表示。
引用这位dalao的一张图：

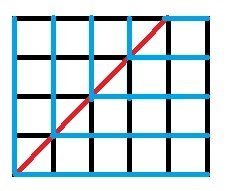
左下角为\((0,0)\)，右上角为\((n,m)\)（设\(n\geq m\)）。题目的每种排列都对应一条从\((n,m)\)走到\((0,0)\)的路径。
那么我们从\((n,m)\)走到\((0,0)\)，每走一条蓝边就表示答对一题。可以发现要走的蓝边数目一定是\(n\)（即\(\max(n,m)\)）。

如果一直在对角线的一侧走，显然成立。
否则至少要答对\(\max(n,m)-\min(n,m)\)题才能到对角线。然后每答错一题，都会导致一定能答对一题，这里一共会答对\(\min(n,m)\)题。所以总共就是\(\max(n,m)\)。

当走到对角线时（两种答案题数相同），会随便猜一个。这时答对的概率为\(\frac 12\)。即对于每个对角线上的点，每次经过期望答对题数都为\(\frac 12\)。
那么我们对每个对角线上的点统计经过它的路径有多少条即可。然后再除以总路径数，再乘以\(\frac 12\)，最后加上\(\max(n,m)\)。

//18ms	7936KB
#include <cstdio>
#include <algorithm>
#define mod 998244353
const int N=1e6;

int fac[N+3],ifac[N+3];

inline int FP(int x,int k)
{
	int t=1;
	for(; k; k>>=1,x=1ll*x*x%mod)
		if(k&1) t=1ll*t*x%mod;
	return t;
}
#define C(n,m) (1ll*fac[n+m]*ifac[n]%mod*ifac[m]%mod)//C(n+m,n)

int main()
{
	int n,m; scanf("%d%d",&n,&m);
	if(n<m) std::swap(n,m);

	int lim=n+m; fac[0]=fac[1]=1;
	for(int i=1; i<=lim; ++i) fac[i]=1ll*fac[i-1]*i%mod;
	ifac[lim]=FP(fac[lim],mod-2);
	for(int i=lim; i; --i) ifac[i-1]=1ll*ifac[i]*i%mod;

	long long ans=0;
	for(int i=1; i<=m; ++i) ans+=1ll*C(i,i)*C(n-i,m-i)%mod;
	ans=ans%mod*FP(C(n,m),mod-2)%mod*FP(2,mod-2)%mod;
	printf("%lld\n",(ans+n)%mod);

	return 0;
}