AGC 018E. Sightseeing Plan(组合 DP)

题目链接

\(Description\)

给定三个不相交的矩形\(A(X1,Y1)-(X2,Y2),B(X3,Y3)-(X4,Y4),C(X5,Y5)-(X6,Y6)\)，求 从第一个矩形中某点\(a\)出发，经过第二个矩形中的某点\(b\)，到达第三个矩形中某点\(c\) 的路径数。\(a,b,c\)有一个不同则路径算作不同。
\(1\leq X1\leq X2<X3\leq X4<X5\leq X6,1\leq Y1\leq Y2<Y3\leq Y4<Y5\leq Y6\)。

\(Solution\)

这个写的挺好。

题目的限制很多，我们考虑简化题目。

令\(C(x,y)\)表示网格图上从\((0,0)\)走到\((x,y)\)的方案数（不是指组合数）。它可以用组合数\(O(1)\)计算。
那么有：

\[\sum_{y=0}^YC(X,y)=C(X+1,Y) \]

（dalao就跳过这吧）
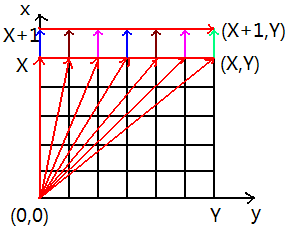
不难理解，大概就是这样（横纵坐标轴画反了QAQ 不建议看这个图 可以自己画画。。）：

设每条路径最后离开\(x=X\)时坐标为\((X,y)(0\leq y\leq Y)\)，那么到\(x=X+1\)后就有唯一的一条路径到达\((X+1,Y)\)，所以对应方案数为\(C(X,y)(0\leq y\leq Y)\)。所以有\(C(X+1,Y)=\sum_{y=1}^YC(X,y)\)。

扩展到二维情况，有：

\[\sum_{x=0}^X\sum_{y=0}^YC(x,y)=C(X+1,Y+1)-1 \]

由刚刚的结论，左边可以写成\(\sum_{x=0}^XC(x+1,Y)=\sum_{x=1}^{X+1}C(x,Y)\)，就是\(C(X+1,Y+1)-1\)。
怎么得到的同上，考虑最后离开\(y=Y\)的位置（不放图了太丑了）。
不过会有\((0,0)\)到\((0,Y)\)再到\((X+1,Y+1)\)的路径（而\(x\neq0\)），因为这条路径是唯一的所以减一即可。

用二维差分就可以将其对应到一个矩形\((X1,Y1)-(X2,Y2)\)上：

\[\sum_{x=X1}^{X2}\sum_{y=Y1}^{Y2}C(x,y)=C(X2+1,Y2+1)-C(X2+1,Y1)-C(X1,Y2+1)+C(X1,Y1) \]

我们可以看出，对于统计一个点到某个矩形内的方案数，可以转化为求该点到四个点的方案数。

对于两个矩形，我们可以\(4\times4\)两两枚举矩形的四个关键点，贡献就是对应方案数乘两个关键点的两个符号。因为可以看做求第二个矩形的四个关键点到第一个矩形的方案数，即右上到左下，所以第一个矩形是拆成\(C(X2,Y2)-C(X2,Y1-1)-C(X1-1,Y2)+C(X1-1,Y1-1)\)（是这样理解吧...不然我就不知道为什么这样了...求指正QAQ）。

对于三个矩形，枚举一三两个矩形的两个关键点后，就成了求给定起点、终点，经过第二个矩形的路径数。
对于每条经过第二个矩形\(len\)个点的路径，对应\(len\)种方案。将\(len\)拆开，我们枚举进入/离开第二个矩形时的横/纵坐标，就可以算\(len\)了。具体是 \(起点到离开点的距离-起点到进入点的距离+1\)（\((0,0)\)到\((x,y)\)经过的点数为\(x+y+1\)）（也可以直接都用\((0,0)\)算到它们的方案不需要用起点\((x1,y1)\)）。
当然距离要乘上\(起点到枚举点的方案数*枚举点到终点的方案数\)。

复杂度\(O(16\max(x,y))\)。

---

改了一下午发现是最底下的g[j]写成g[i]了？？？

---

//862ms	15744KB
#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
#define mod 1000000007
#define Add(x,v) (x+=v)>=mod&&(x-=mod)
typedef long long LL;
const int N=2e6;

int fac[N+3],ifac[N+3];

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}
inline int FP(int x,int k)
{
	int t=1;
	for(; k; k>>=1,x=1ll*x*x%mod)
		if(k&1) t=1ll*t*x%mod;
	return t;
}
#define C(n,m) (1ll*fac[n+m]*ifac[n]%mod*ifac[m]%mod)//C(n+m,n)
int Calc(int x1,int y1,int sign1,int x2,int y2,int sign2,int X3,int X4,int Y3,int Y4)
{//(x1,y1)->(x2,y2)
	LL res=0;
	for(int x=X3; x<=X4; ++x)
		Add(res,1ll*(x+Y4+1)*C(x-x1,Y4-y1)%mod*C(x2-x,y2-Y4-1/*强制下一步离开y=Y4*/)%mod),
		Add(res,mod-1ll*(x+Y3)*C(x-x1,Y3-y1-1/*强制最后一步是到达y=Y3*/)%mod*C(x2-x,y2-Y3)%mod);
//		Add(res,1ll*(x-x1+Y4-y1+1)*C(x-x1,Y4-y1)%mod*C(x2-x,y2-Y4-1)%mod),
//		Add(res,mod-1ll*(x-x1+Y3-y1)*C(x-x1,Y3-y1-1)%mod*C(x2-x,y2-Y3)%mod);
	for(int y=Y3; y<=Y4; ++y)
		Add(res,1ll*(y+X4+1)*C(y-y1,X4-x1)%mod*C(y2-y,x2-X4-1)%mod),
		Add(res,mod-1ll*(y+X3)*C(y-y1,X3-x1-1)%mod*C(y2-y,x2-X3)%mod);
//		Add(res,1ll*(y-y1+X4-x1+1)*C(y-y1,X4-x1)%mod*C(y2-y,x2-X4-1)%mod),
//		Add(res,mod-1ll*(y-y1+X3-x1)*C(y-y1,X3-x1-1)%mod*C(y2-y,x2-X3)%mod);

	res%=mod;
	return sign1*sign2*res;
}

int main()
{
	fac[0]=fac[1]=1, ifac[N]=407182070;
	for(int i=2; i<=N; ++i) fac[i]=1ll*fac[i-1]*i%mod;
	for(int i=N; i; --i) ifac[i-1]=1ll*ifac[i]*i%mod;

	static int f[4][3],g[4][3];

	int x1=read(),x2=read(),x3=read(),x4=read(),x5=read(),x6=read(),
		y1=read(),y2=read(),y3=read(),y4=read(),y5=read(),y6=read();

	f[0][0]=x1-1, f[0][1]=y1-1, f[0][2]=1;
	f[1][0]=x2, f[1][1]=y1-1, f[1][2]=-1;
	f[2][0]=x1-1, f[2][1]=y2, f[2][2]=-1;
	f[3][0]=x2, f[3][1]=y2, f[3][2]=1;

	g[0][0]=x5, g[0][1]=y5, g[0][2]=1;
	g[1][0]=x6+1, g[1][1]=y5, g[1][2]=-1;
	g[2][0]=x5, g[2][1]=y6+1, g[2][2]=-1;
	g[3][0]=x6+1, g[3][1]=y6+1, g[3][2]=1;

	LL ans=0;
	for(int i=0; i<4; ++i)
		for(int j=0; j<4; ++j)
			ans+=Calc(f[i][0],f[i][1],f[i][2],g[j][0],g[j][1],g[j][2],x3,x4,y3,y4);
	printf("%lld\n",(ans%mod+mod)%mod);

	return 0;
}