BZOJ.4237.稻草人(CDQ分治 单调栈)

题目链接
dbzoj

---

\(Description\)
平面上有\(n\)个特殊点，求有多少个矩形，满足其左下角、右上角为特殊点，其内部（不含边界）没有特殊点。
\(n\leq 2\times10^5\)。

\(Solution\)
考虑分治，消掉一维。
把所有点按\(y\)排序，然后我们平行于x轴切一刀，将平面分成上下两部分，考虑上与下产生的答案（即右上角在上半部分，左下角在下半部分）。
然后我们对上下两部分点分别按\(x\)排序。
上面的点会受它前面\(x,y\)均比它小的点的影响。所以对上半部分我们需要维护\(y_j\)比当前小的最大的\(x_j\)，可以用单调栈。
而下半部分的点也会互相影响，我们发现可行点的\(y\)递减，它们都有可能（不受上面某点影响）成为答案。
同样维护单调栈。对于上半部分内的限制，在单调栈中二分一个位置就好了。

如图：

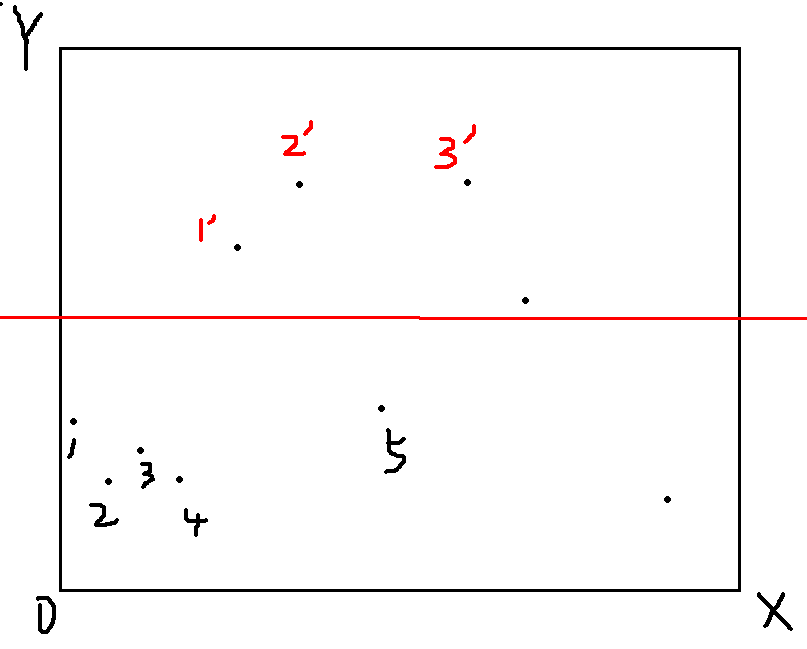
计算1'时，下面的点2会被3,4覆盖；2'的计算会被1'影响；5会覆盖下面前面所有点......

实现：
每次CDQsort三遍太暴力了。虽然可过，但是常数大了(不止一点：5800kb 15748ms)。
先按x排序，然后CDQ时按y归并排序，分成两部分。这样在同一部分的点一定还是按x排好序的。然后分治处理同一部分的点。但是这样不好找分割的位置，要离散化纵坐标，l,r表示y轴区间。
或者可以先按y排序，处理完后把上下两部分点按x归并起来，这样同一部分的点的x是有序的，同时也保证前一部分的y都比后一部分的y小。

---

//7368kb	3696ms
#include <cstdio>
#include <cctype>
#include <algorithm>
//#define gc() getchar()
#define MAXIN 300000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
const int N=2e5+5;

long long Ans;
char IN[MAXIN],*SS=IN,*TT=IN;
struct Point
{
	int x,y;
}p[N],tmp[N],sk1[N],sk2[N];

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}
inline bool cmpx(const Point &a,const Point &b)
{
	return a.x<b.x;
}
inline bool cmpy(const Point &a,const Point &b)
{
	return a.y<b.y;
}
void CDQ(int l,int r)
{
	if(l==r) return;
	int mid=l+r>>1;
	CDQ(l,mid), CDQ(mid+1,r);

	for(int now=l,top1=0,top2=0,i=mid+1; i<=r; ++i)
	{
		int xn=p[i].x,yn=p[i].y;
		while(top1 && sk1[top1].y>=yn) --top1;
		sk1[++top1]=p[i];

		while(now<=mid && p[now].x<xn)
		{
			int yy=p[now].y;
			while(top2 && sk2[top2].y<=yy) --top2;//其实题目已保证yi互不相同...
			sk2[++top2]=p[now], ++now;
		}

		int xx=sk1[top1-1].x,L=1,R=top2,M,res=top2+1;
		while(L<=R)
		{
			if(sk2[M=L+R>>1].x>=xx) res=M, R=M-1;//not mid...
			else L=M+1;
		}
		Ans+=top2-res+1;
	}
	for(int i=l,a=l,b=mid+1; i<=r; ++i)
		tmp[i]=((a<=mid&&p[a].x<p[b].x)||b>r)?p[a++]:p[b++];
	for(int i=l; i<=r; ++i) p[i]=tmp[i];
}

int main()
{
	int n=read();
	for(int i=1; i<=n; ++i) p[i]=(Point){read(),read()};
	std::sort(p+1,p+1+n,cmpy);
	sk1[0].x=sk2[0].x=-1, CDQ(1,n), printf("%lld\n",Ans);

	return 0;
}