9.16 牛客提高集训营2
2018.9.16 牛客提高集训营2
期望得分:100+40+10
实际得分:100+10+10
非要用滚动数组,还不好好清空,丢了30分吧。
A 方差
拆一下方差的式子就可以\(O(1)\)得到要求的值了。
出题人:数据是精心设计的,刚好不会爆longlong。
是的,这是在你原题面乘\(n-1\)而不是乘\((n-1)^2\)的情况下。
longlong不好爆吗,\((10^4)^2\times 10^5\times 10^5\times 10^5=GG\)。so数据(故意)水差评。
输出格式真心有毒。
#include <cstdio>
#include <cctype>
#include <iostream>
#define gc() getchar()
typedef long long LL;
const int N=1e5+5;
int n,A[N];
inline int read()
{
int now=0,f=1;register char c=gc();
for(;!isdigit(c);c=='-'&&(f=-1),c=gc());
for(;isdigit(c);now=now*10+c-'0',c=gc());
return now*f;
}
//void print(__int128 x)
//{
// if(x<0) {x=-x; putchar('-');}
// if(x>9) print(x/10);
// putchar(x%10+'0');
//}
int main()
{
n=read(); LL s1=0,s2=0;
for(int i=1; i<=n; ++i) s1+=(A[i]=read()),s2+=A[i]*A[i];
// if(n>2000)
// {
// __int128 ss1=s1,ss2=s2;
// for(int i=1; i<n; ++i)
// {
// __int128 aver2=ss1-A[i],tmp=ss2-A[i]*A[i];
// print(tmp*(n-1)-aver2*aver2), putchar(' ');
// }
// __int128 aver2=ss1-A[n],tmp=ss2-A[n]*A[n];
// print(tmp*(n-1)-aver2*aver2), putchar('\n');
// }
// else
{
for(int i=1; i<n; ++i)
{
LL aver2=s1-A[i];
printf("%lld ",1ll*(n-1)*(s2-A[i]*A[i])-aver2*aver2);
}
LL aver2=s1-A[n];
printf("%lld\n",1ll*(n-1)*(s2-A[n]*A[n])-aver2*aver2);
}
return 0;
}
B 分糖果(容斥 DP 单调栈)
先考虑拆环为链,序列上怎么做。
有限制不好做,考虑容斥。\(Ans=无限制方案数-存在相邻至少2个相同+存在相邻至少3个相同\ldots\)
每次确定相邻多少个相同就是分一段,这一段的方案数显然为这一段\(A_i\)的最小值。
\(f_i\)表示考虑到\(i\)的答案。于是得到转移方程:$$f_i=\sum_{j<i}f_j\times\min{a_{j+1},\ldots,a_i}\times(-1)^{i-j-1}$$\(i-j-1\)即(这一段)有多少个相同。
(或者我们考虑,第\(i\)个随便放:\(f_i=f_{i-1}\times A_i\),这样多算了\(i\)与\(i+1\)相同的情况,所以再减去\(f_{i-2}\times\min(A_i,A_{i-1})\),...)
首先把\((-1)^i\)提出来:$$f_i=(-1)^i\times\sum_{j<i}\min{a_{j+1},\ldots,a_i}\times f_j\times(-1)^{j+1}$$
后面只与\(j\)有关。考虑怎么维护。当从\(i\)转移到\(i+1\)时:\(\min\{a_{j+1},\ldots,a_i\}\to\min\{a_{j+1},\ldots,a_{i+1}\}\),只改变一项,可以用线段树取min、求和做。
我们实际是在每个位置维护一个后缀最小值。
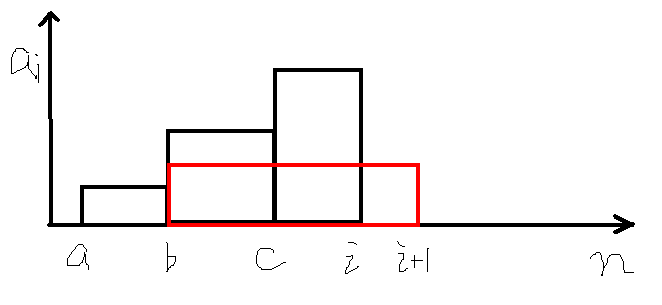
如图,当添加\(i+1\)时,会使\(a\sim i+1\)的最小值改变,即把\(b\sim c,c\sim i\)这两段删去,添加新的一段\(a\sim i+1\)。可以用单调栈维护。
然后是环的问题。即若\(1\)和\(n\)相同则不合法。
我们可以用不考虑环的\(f[n]\),减去不考虑环的\(f[n-1]\),即直接让\(1\)和\(n\)相等(即不合法方案数)。但是又会多减(不用想感觉应该是这样...),所以再加\(f[n-3]\)......
还有个问题是合并时\(a_1,a_n\)是否可以取值相同。可以把最小的\(A_i\)转到\(A_1\)位置,这样就可以直接和最后一段合并。
坑
C 集合划分(构造)
\(m=0\)时
用\(lb(x)=lowbit(x)\)表示\(x\)二进制下最低位的\(1\),即\(x\)集合内标号最小的元素。用\(x|y\)表示集合\(x\)与\(y\)的并。
那么:把\(lb(x)\)相同的元素全部分给一个人,这样构造的方案一定是合法的。
证明:因为\(lb(x|y)\)一定等于\(lb(x)\)或\(lb(y)\),所以若集合\(x,y\)都属于A,集合\(x|y\)也一定属于A。
\(lb(x)=i\)的\(x\)的个数恰好有\(2^{n-i}\)个(比\(i\)大的\(n-i\)个元素任选),可以直接对\(K\)二进制拆分。
\(m>0\)时
把上述做法推广,我们给每个元素定义一个优先级,使得不同元素优先级不同。
然后对于一个集合,定义其"特征"为其中优先级最高的元素的编号。
那么把特征相同的集合全部分给一个人,这样构造的方案一定是合法的。
同时我们可以证明,对于所有方案都可以用这种方法构造。
证明:
假设 \(\{1,2,\dots, n\}\in S\)
那么一定存在一个 \(i\) ,使得 \(\forall U\) 使得 \(i\in U\), 必有 \(U\in S\) .
(如果不存在,那么 \(\forall i, \exists i\in V_i, V_i\in T\) ,那么\(\{1,2,\dots, n\}=\bigcup_i V_i \in T\),矛盾)
不失一般性,交换\(S,T\)也成立。
那么问题有两个:1.确定每个元素的优先级,从而计算集合的特征;2.把特征相同的集合分给同一个人。
因为有\(K\)限制,哪些集合分给谁是确定的,即第二个问题不需要考虑。
然后第一个问题我就看不懂了。
求路过dalao解答


坑
考试代码
B
#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
#define MAXIN 300000
//#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
#define Mod(x) x>=mod&&(x-=mod)
#define mod 1000000007
typedef long long LL;
const int N=1e5+5;//1e6+5
int n,A[N],ref[N],f[2][1005][1005];
char IN[MAXIN],*SS=IN,*TT=IN;
inline int read()
{
int now=0;register char c=gc();
for(;!isdigit(c);c=gc());
for(;isdigit(c);now=now*10+c-'0',c=gc());
return now;
}
inline int Find(int x,int r)
{
int l=1,mid;
while(l<r)
if(ref[mid=l+r>>1]<x) l=mid+1;
else r=mid;
return l;
}
inline int FP(int x,int k)
{
int t=1;
for(; k; k>>=1,x=1ll*x*x%mod)
if(k&1) t=1ll*t*x%mod;
return t;
}
bool Spec1()
{
int a=A[1];
for(int i=2; i<=n; ++i) if(A[i]!=a) return 0;
LL ans=0; int pw=a-1;
for(int i=1; i<=n-3; ++i,pw=1ll*pw*(a-1)%mod)
if((n-i)&1) ans+=1ll*a*pw%mod;
else ans-=1ll*a*pw%mod;
ans-=1ll*a*pw%mod;
pw=1ll*pw*(a-1)%mod, ans+=1ll*a*pw%mod;
printf("%d\n",(int)((ans%mod+mod)%mod));
return 1;
}/*
8 10 10 10 10 10 10 10 10
43046730*/
int main()
{
n=read();
for(int i=1; i<=n; ++i) ref[i]=A[i]=read();
if(n>100 && Spec1()) return 0;
// std::sort(ref+1,ref+1+n); int cnt=1;
// for(int i=2; i<=n; ++i) if(ref[i]!=ref[i-1]) ref[++cnt]=ref[i];
// for(int i=1; i<=n; ++i) A[i]=Find(A[i],cnt);
if(n>2000) return putchar('0'),0;
int now=0,las=1;
for(int i=1,a1=A[1]; i<=a1; ++i) f[las][i][i]=1;
for(int i=2,a1=A[1]; i<=n; ++i)
{
int lc=A[i-1],nc=A[i];
for(int j=1; j<=a1; ++j)
{
LL sum=0;
for(int k=1; k<=lc; ++k) sum+=f[las][j][k];
for(int k=lc+1; k<=nc; ++k) f[las][j][k]=0;//!!!
sum%=mod;
// if(!sum) continue;//...
for(int k=1; k<=nc; ++k) f[now][j][k]=(sum-f[las][j][k]+mod)%mod;
}
now=las, las^=1;
}
LL ans=0;
for(int i=1,a1=A[1]; i<=a1; ++i)
for(int j=1,an=A[n]; j<=an; ++j)
if(i!=j) ans+=f[las][i][j];
printf("%d\n",(int)(ans%mod));
return 0;
}
C
#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
const int N=(1<<18)+5;
int n,m,lim,K,A[10005];
bool OK,chose[N],need[N],inq[N];
char ans[N];
inline int read()
{
int now=0;register char c=gc();
for(;!isdigit(c);c=gc());
for(;isdigit(c);now=now*10+c-'0',c=gc());
return now;
}
void DFS(int x,int sum)
{
if(OK) return;
if(x>lim)
{
if(sum!=K) return;
for(int s1=1; s1<=lim; ++s1)
if(chose[s1])
for(int s2=1; s2<=lim; ++s2)
if(chose[s2] && !chose[s1|s2]) return;
OK=1;
for(int s=1; s<=lim; ++s) if(chose[s]) ans[s]='1';
return;
}
if(need[x])
{
if(sum>=K) return;
chose[x]=1, DFS(x+1,sum+1), chose[x]=0;
}
else
{
if(sum<K) chose[x]=1, DFS(x+1,sum+1), chose[x]=0;
DFS(x+1,sum);
}
}
bool Check1()
{
static int q[N];
int h=0,t=0;
for(int i=1; i<=m; ++i) q[++t]=A[i],inq[A[i]]=1;
while(h<t)
{
int x=q[++h];
for(int i=1; i<=t; ++i)
if(!inq[x|q[i]]) inq[q[++t]=x|q[i]]=1;
}
if(t>K) return 0;
return 1;
}
int main()
{
n=read(),m=read(),K=read(),lim=(1<<n)-1;
for(int s=0; s<=lim; ++s) ans[s]='0'; ans[lim+1]='\0';
for(int i=1; i<=m; ++i) need[A[i]=read()]=1;
if(m>K) return printf("-1"),0;
if(n<=4)
{
DFS(1,0);
if(OK)
{
for(int i=1; i<=lim; ++i) putchar(ans[i]);
// ans[lim+1]='\0', puts(ans+1);//mdzz
}
else printf("-1");
return 0;
}
if(1||!Check1()) return printf("-1"),0;
return 0;
}
别来无恙 你在心上
------------------------------------------------------------------------------------------------------------------------


 浙公网安备 33010602011771号
浙公网安备 33010602011771号