Codeforces.643E.Bear and Destroying Subtrees(DP 期望)

题目链接

\(Description\)

有一棵树。Limak可以攻击树上的某棵子树，然后这棵子树上的每条边有\(\frac{1}{2}\)的概率消失。定义 若攻击以\(x\)为根的子树，高度\(ht(x)\)为\(x\)子树剩余点(与x连通)的最大深度。共\(q\)次操作，两种：
\(1\ x\).新建一个节点，其父节点为\(x\)。
\(2\ x\).询问若攻击以\(x\)为根的子树，\(x\)子树的期望高度。
\(q\leq 5\times10^5\)。允许有一定精度误差。

\(Solution\)

首先我们不需要考虑很大的高度\(h\)，假如\(h=100\)，同时存在\(100\)条边的概率非常小。先假设需考虑的最大高度\(MAX\_H=60\)。
对于询问，只要\(x\)有一个子树的高度为\(h\)且其它子树高度不超过\(h\)，就可以用\(p*h\)更新答案。
so记\(f[x][h]\)表示以\(x\)为根，\(ht(x)\leq h\)的概率。则答案为\(\sum_{h=1}^{MAX\_H}h\times(f[x][h]-f[x][h-1])\)。
对于新建节点，沿着\(fa\)一直更新最多\(MAX\_H\)次。
\(f[x][h]\)自然是从\(f[son_x][h-1]\)转移。每个子节点\(v\)有两种情况，一是存在边，对\(f[x][h]\)贡献\(\frac{1}{2}\times f[v][h-1]\)；二是不存在该边，概率为\(\frac{1}{2}\)。
更新时当然不能\(2^n\)枚举子节点。类似多项式，把\(n\)项乘在一起，即

\[f[x][h]=\prod_{v=son_x}(\frac{1}{2}+\frac{1}{2}f[v][h-1]) \]

所以更新的时候把原来的项除掉再乘上新的项就可以了。

对于\(MAX\_H\)的取值，你可能会认为\(30\)就足够了，因为\(\frac{1}{2^{30}}\)已经足够小。事实上，考虑一个菊花图，从根节点延伸出\(\frac{n}{31}\)条路径，且每条路径长度为\(31\)。那么以\(1\)为根树深为\(31\)的概率为：

\[1-(1-\frac{1}{2^{31}})^{\frac{n}{31}} \]

这是大于\(10^{-6}\)的。
http://www.wolframalpha.com/input/?i=1+-+(1-(1%2F2)%5Ed)%5E(N%2Fd)+for+N+%3D+500000+and+d+%3D+31

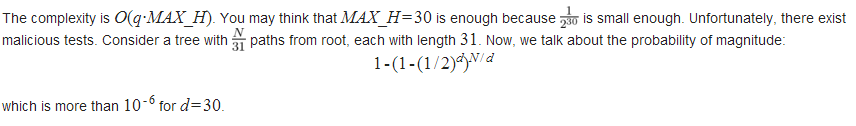
复杂度\(O(q*MAX\_H)\)

#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
#define MAX_H 60
const int N=5e5+5;

int n,fa[N];
double f[N][MAX_H];

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}

int main()
{
	n=1;
	for(int i=0; i<MAX_H; ++i) f[1][i]=1;
	for(int Q=read(),x; Q--; )
	{
		if(read()==1)
		{
			fa[++n]=x=read();
			for(int i=0; i<MAX_H; ++i) f[n][i]=1;
			double tmp1=f[x][0],tmp2;
			f[x][0]*=0.5;//深度还是不超过1啊 
			for(int Fa=fa[x],i=1; Fa&&i<MAX_H; Fa=fa[x=Fa],++i)
			{
				tmp2=f[Fa][i];
				f[Fa][i] /= 0.5 + 0.5*tmp1;
				f[Fa][i] *= 0.5 + 0.5*f[x][i-1];
				tmp1=tmp2;
			}
		}
		else
		{
			x=read(); double ans=0;
			for(int i=1; i<MAX_H; ++i) ans+=(f[x][i]-f[x][i-1])*i;
			printf("%.10lf\n",ans);
		}
	}
	return 0;
}