Codeforces Round #493 (Div 2) (A~E)

目录

• Codeforces 998
  • A.Balloons
  • B.Cutting
  • C.Convert to Ones
  • D.Roman Digits
  • E.Sky Full of Stars(容斥 计数)

---

Codeforces 998

比赛链接

A.Balloons

输出啥看错WA\(*2\)+第一次写sort写了cmp()但是没加cmpWA\(*2\)（结构体重载运算符后遗症）。。
没谁了。

#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
const int N=150;

int n,A[N];

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}

int main()
{
	n=read(); int pos=1,sum=0;
	for(int i=1; i<=n; ++i)
		sum+=(A[i]=read()), A[pos]>A[i]&&(pos=i);
	sum-=A[pos];
	if(sum<=A[pos]) puts("-1");
	else
	{
		printf("%d\n",n-1);
		for(int i=1; i<=n; ++i) if(i!=pos) printf("%d ",i);
	}

	return 0;
}

B.Cutting

能切割的位置显然确定。

#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
const int N=1004;

int n,B,A[N],c[N];

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}

int main()
{
	n=read(),B=read();
	int cnt=0;
	for(int i=1; i<=n; ++i) A[i]=read();
	for(int i=1,odd=0,even=0; i<=n; ++i)
	{
		if(A[i]&1) ++odd; else ++even;
		if(odd==even&&i!=n) c[++cnt]=std::abs(A[i+1]-A[i]);
	}
	std::sort(c+1,c+1+cnt);
	int res=0;
	for(int i=1; i<=cnt; ++i)
		if(B>=c[i]) ++res, B-=c[i];
		else break;
	printf("%d",res);

	return 0;
}

C.Convert to Ones

如果X,Y的大小关系确定，那可以完全利用小的那个。即策略只有两种：把所有0换在一起，一次反转；反转所有段的0。统计有多少段0即可。
当时闲的数了一下1的段数，然后就把zero和one写反了，然后就被MainTest给×了==。

#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
using std::min;
typedef long long LL;
const int N=4e5+7;
const LL INF=1e17;

int n;
LL X,Y;
char s[N];

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}

int main()
{
	n=read(), X=read(), Y=read(), scanf("%s",s+1);
	int cnt=0;
	for(int i=1; i<=n; ++i) if(s[i]=='0') ++cnt;
	if(!cnt) return putchar('0'),0;//判1的话还要判一下这个...
	if(cnt==n) return printf("%I64d",Y),0;

	LL zero=0,one=0;
	if(s[1]=='0') ++zero; else ++one;
	for(int i=2; i<=n; ++i)
		if(s[i]=='1'&&s[i-1]=='0') ++one;
		else if(s[i]=='0'&&s[i-1]=='1') ++zero;
	printf("%I64d",min((zero-1ll)*X+Y,min(zero*Y,min((one-1ll)*X+2ll*Y,one*Y+Y))));

	return 0;
}

---

比赛结束后

D.Roman Digits

由于序列长度n是固定的，我们可以假设最初有n个1，然后用5,10,50去替换，即求从{0,4,9,49}中选n个数能组成多少个不同的。
先看{0,4,9}。问题在于一个数可以有多种表示。在使用4的个数大于9之后，一部分4是可以用9替换的，多余的位置用0补。
所以如果暴力的话，4的个数只需从0枚举到min(n,8)，然后选一些9，这样每次都能组成一个不同的数。
对于{0,4,9,49}，可以用类似方法暴力计算(9只需要枚举到min(n,48)吗...并不清楚)。
打表后可以发现，n>=12时，n每加一，组成数的个数+49，即都能组成。然后只需要算n<=12的就OK了。
嗯。。不会证。

还有种思路(Way2)：
我们考虑一下有多种表示的数字的可能。可以先通过打表找到有多种表示的数字，能发现从45往后都可以。(然而好像并没什么用)

\[9*5 = 4*10 + 5*1\\ 9*10 = 1*50 + 8*5\\ 5*10 + 1*5 = 1*50 + 5*1\]

这意味着我们不需要 超过8个的5、超过8个的10、超过4个的10且至少1个5。那枚举时范围就很小了。
后面没看明白 不写了。。

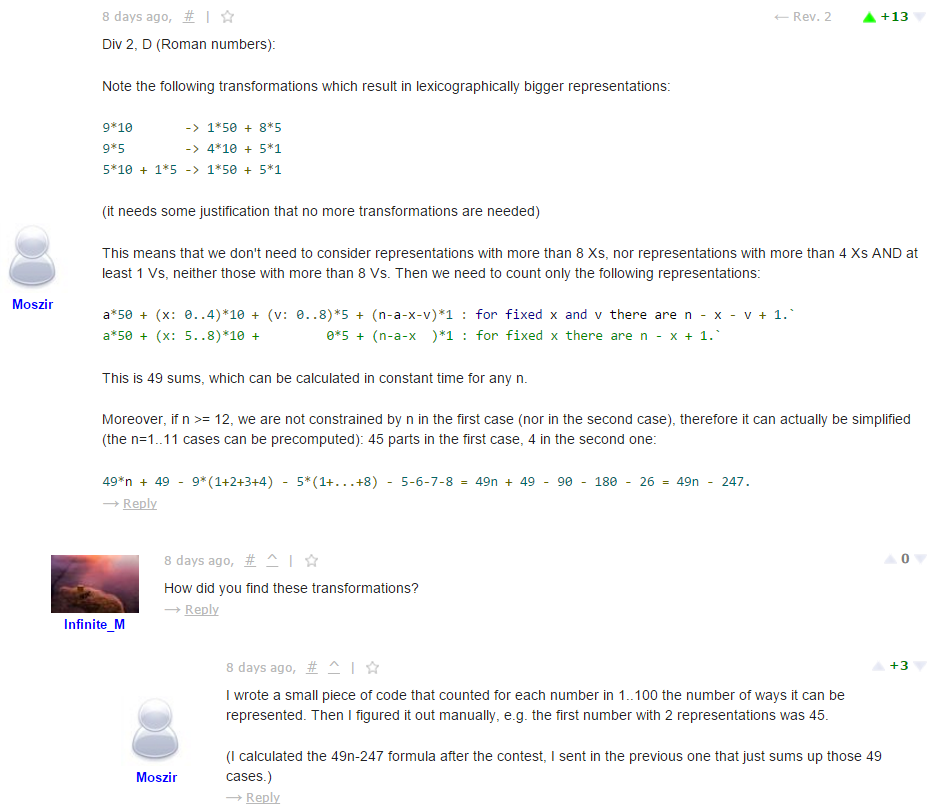
还有一种思路：

找到个证明（然而没啥用 也不想看 先粘这了）：

#include <cstdio>
#include <cstring>
#include <algorithm>
const int N=1e4+5;
const int Ans[17]={0,4,10,20,35,56,83,116,155,198,244,292,341,390};

namespace Way2
{
	bool use[200];
	int Judge(int n)
	{
		memset(use,0,sizeof use);
		for(int i=0; i<=20; ++i)
			for(int j=0; j<=20; ++j)
				for(int k=0; k<=20; ++k)
					for(int l=0; l<=20; ++l)
						if(i+j*5+k*10+l*50==n && use[i+j+k+l]) return 1;
						else if(i+j*5+k*10+l*50==n) use[i+j+k+l]=1;// printf("%d=%d+%d*5+%d*10+%d*50\n",n,i,j,k,l);
		return 0;
	}
	void Main()
	{
		for(int i=1; i<=100; ++i)
			if(Judge(i)) printf("%d\n",i);	
	}
}

long long Calc(int n)
{
	return Ans[n];
	static bool vis[N];
	memset(vis,0,sizeof vis);
	long long ans=0;
	for(int i=0; i<=8; ++i)
		for(int j=0; j<=8; ++j)
			for(int k=0; k<=48; ++k)//我也不知道最小可以枚举到多少...大点吧 
				if(i+j+k<=n && !vis[i*4+j*9+k*49])
					vis[i*4+j*9+k*49]=1, ++ans;
	return printf("%d:",n),ans;
}

int main()
{
	int n; scanf("%d",&n);
	if(n<=12) printf("%I64d\n",Calc(n));
	else printf("%I64d\n",Calc(12)+1ll*(n-12)*49);

	return 0;
}

E.Sky Full of Stars(容斥 计数)

单独写一篇，见这儿。

//1107ms	7700KB
#include <cstdio>
#include <algorithm>
#define mod (998244353)
typedef long long LL;
const int N=1e6+7;

int C[N],inv[N];

inline LL FP(LL x,int k)
{
	LL t=1;
	for(; k; k>>=1,x=x*x%mod)
		if(k&1) t=t*x%mod;
	return t;
}

int main()
{
	int n; scanf("%d",&n);
	LL ans1=0; C[0]=inv[1]=1;
	for(int i=1; i<=n; ++i)
	{
		if(i>1) inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
		C[i]=1ll*(n-i+1)*C[i-1]%mod*inv[i]%mod;
		if(i&1) ans1+=1ll*C[i]*FP(3,(1ll*n*(n-i)+i)%(mod-1))%mod;//a^{\varphi(p)}=1(\mod p)
		else ans1-=1ll*C[i]*FP(3,(1ll*n*(n-i)+i)%(mod-1))%mod;
	}
	ans1=2ll*ans1%mod;
	LL ans2=0;
	for(int i=0,pw3=1; i<n; ++i)
	{
		if(i&1) ans2+=1ll*C[i]*(FP(1+mod-pw3,n)-FP(mod-pw3,n))%mod;
		else ans2-=1ll*C[i]*(FP(1+mod-pw3,n)-FP(mod-pw3,n))%mod;
		pw3=3ll*pw3%mod;
	}
	printf("%I64d\n",((ans1+3ll*ans2)%mod+mod)%mod);

	return 0;
}