BZOJ.2716.[Violet3]天使玩偶(K-D Tree)

BZOJ
洛谷

---

\(Description\)
二维平面上初始有\(n\)个点，\(m\)次\(2\)种操作：在二维平面上加一个点；询问离某个点曼哈顿距离最近的点是多少。
\(n,m\leq3\times10^5\)。

\(Solution\)
KD-Tree。因为插入过多点后可能会退化成链，所以\(\text{左/右子树的size} \gt α\times\text{整棵子树的size}\)时，对整棵子树进行重构。

树的节点数必须是3n？why？洛谷BZOJ都这样（应该是数据范围错了吧 和SYJ摆棋子一样n=5e5）
但是n=5e5 为什么仍要3倍空间（如果重构）迷。

吊打CDQ。

---

PS：
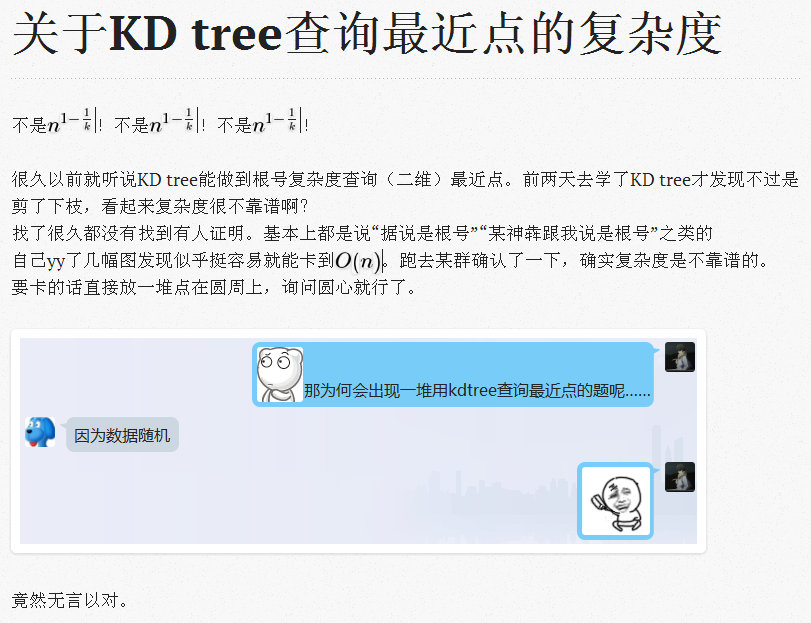
不确定实际复杂度，可以google一下
图片来源：http://dwjshift.logdown.com/posts/306502

---

//65280kb	14368ms
#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
#define alpha (0.75)
const int N=(3e5+5),INF=0x7fffffff;

int n,Q,root,D_now,Ans,top,sk[N*2];

struct Point{
	int d[2];
}p[N*2];
struct Node{
	int ls,rs,sz,Min[2],Max[2];
	Point pt;
}t[N*3];//?

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}
inline bool cmp(const Point &a,const Point &b){
	return a.d[D_now]<b.d[D_now];//||(a.d[D_now]==b.d[D_now]&&a.d[D_now^1]<b.d[D_now^1]);
}
inline int New_Node(){
	return top?sk[top--]:++n;
}
inline void Init(int rt){
	for(int i=0; i<2; ++i)
		t[rt].Min[i]=t[rt].Max[i]=t[rt].pt.d[i];
}
inline void Update(int rt)
{
	int ls=t[rt].ls,rs=t[rt].rs;
	t[rt].sz=t[ls].sz+t[rs].sz+1;
	for(int i=0; i<2; ++i){
		if(ls) t[rt].Min[i]=std::min(t[rt].Min[i],t[ls].Min[i]), t[rt].Max[i]=std::max(t[rt].Max[i],t[ls].Max[i]);
		if(rs) t[rt].Min[i]=std::min(t[rt].Min[i],t[rs].Min[i]), t[rt].Max[i]=std::max(t[rt].Max[i],t[rs].Max[i]);
	}
}
int Build(int l,int r,int D)
{
	if(l>r) return 0;
	int mid=l+r>>1, k=New_Node();
	D_now=D, std::nth_element(p+l,p+mid,p+r+1,cmp);
	t[k].pt=p[mid], Init(k);
	t[k].ls=Build(l,mid-1,D^1), t[k].rs=Build(mid+1,r,D^1);
	Update(k); return k;
}
void DFS(int rt,int num)
{
	if(t[rt].ls) DFS(t[rt].ls,num);
	p[num+t[t[rt].ls].sz+1]=t[rt].pt, sk[++top]=rt;
	if(t[rt].rs) DFS(t[rt].rs,num+t[t[rt].ls].sz+1);
}
inline void Check(int &k,int D){
	if(alpha*t[k].sz<t[t[k].ls].sz||alpha*t[k].sz<t[t[k].rs].sz)
		DFS(k,0), k=Build(1,t[k].sz,D);
}
void Insert(Point p,int &k,int D)
{
	if(!k) {t[k=New_Node()].pt=p, Init(k), t[k].sz=1, t[k].ls=t[k].rs=0; return;}
	if(p.d[D]<=t[k].pt.d[D]) Insert(p,t[k].ls,D^1);
	else Insert(p,t[k].rs,D^1);
	Update(k), Check(k,D);
}
int Get_dis(Point p,int k)//Manhattan Distance
{
	int res=0;
	for(int i=0; i<2; ++i)
		res+=std::max(0,p.d[i]-t[k].Max[i])+std::max(0,t[k].Min[i]-p.d[i]);
	return res;
}
inline int Dis(Point a,Point b){
	return std::abs(a.d[0]-b.d[0])+std::abs(a.d[1]-b.d[1]);
}
void Query(Point p,int k)//Manhattan Distance
{
	Ans=std::min(Ans,Dis(t[k].pt,p));
	int dl=t[k].ls?Get_dis(p,t[k].ls):INF;
	int dr=t[k].rs?Get_dis(p,t[k].rs):INF;
	if(dl<dr){
		if(dl<Ans) Query(p,t[k].ls);
		if(dr<Ans) Query(p,t[k].rs);
	}
	else{
		if(dr<Ans) Query(p,t[k].rs);
		if(dl<Ans) Query(p,t[k].ls);
	}
}

int main()
{
	n=read(),Q=read();
	for(int i=1; i<=n; ++i) p[i].d[0]=read(),p[i].d[1]=read();
	root=Build(1,n,0); int x,y; Point tmp;
	while(Q--)
		if(read()==1) tmp.d[0]=read(),tmp.d[1]=read(),Insert(tmp,root,0);
		else tmp.d[0]=read(),tmp.d[1]=read(),Ans=INF,Query(tmp,root),printf("%d\n",Ans);

	return 0;
}

2018.5.21 又写了遍，常数好像小了？(然并软)

//65280kb	14264ms(fread:65576kb	12412ms)
#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
#define alpha (0.75)
const int N=5e5+5,INF=0x7fffffff;

namespace KD_Tree
{
	int n,Q,root,Now_d,top,sk[N<<1],Ans;
	struct Point{
		int d[2];
	}p[N<<1];
	struct Node{
		int Min[2],Max[2],ls,rs,sz;
		Point pt;
	}t[N*3];//??
	
	inline bool Cmp_d(const Point &a,const Point &b){
		return a.d[Now_d]<b.d[Now_d];
	}
	inline int New_Node(){
		return top?sk[top--]:++n;
	}
	inline void Init(int rt)
	{
		t[rt].sz=1;
		for(int i=0; i<2; ++i)
			t[rt].Min[i]=t[rt].Max[i]=t[rt].pt.d[i];
	}
	inline void Update(int rt)
	{
		int ls=t[rt].ls,rs=t[rt].rs;
		t[rt].sz=t[ls].sz+t[rs].sz+1;
		for(int i=0; i<2; ++i){
			if(ls) t[rt].Min[i]=std::min(t[rt].Min[i],t[ls].Min[i]),t[rt].Max[i]=std::max(t[rt].Max[i],t[ls].Max[i]);
			if(rs) t[rt].Min[i]=std::min(t[rt].Min[i],t[rs].Min[i]),t[rt].Max[i]=std::max(t[rt].Max[i],t[rs].Max[i]);
		}
	}
	int Build(int l,int r,int D)
	{
		if(l>r) return 0;
		int mid=l+r>>1,k=New_Node();
		Now_d=D, std::nth_element(p+l,p+mid,p+r+1,Cmp_d);
		t[k].pt=p[mid], Init(k);
		t[k].ls=Build(l,mid-1,D^1), t[k].rs=Build(mid+1,r,D^1);
		Update(k); return k;
	}
	void DFS(int rt,int num)
	{
		if(t[rt].ls) DFS(t[rt].ls,num);
		p[num+t[t[rt].ls].sz+1]=t[rt].pt, sk[++top]=rt;
		if(t[rt].rs) DFS(t[rt].rs,num+t[t[rt].ls].sz+1);
	}
	inline void Check(int &k,int D){
		if(t[k].sz*alpha<t[t[k].ls].sz||t[k].sz*alpha<t[t[k].rs].sz)
			DFS(k,0), k=Build(1,t[k].sz,D);
	}
	void Insert(Point p,int &k,int D)
	{
		if(!k) {t[k=New_Node()].pt=p, Init(k), t[k].ls=t[k].rs=0; return;}
		if(p.d[D]<=t[k].pt.d[D]) Insert(p,t[k].ls,D^1);
		else Insert(p,t[k].rs,D^1);
		Update(k), Check(k,D);
	}
	int Dis_node(Point a,int k)
	{
		int res=0;
		for(int i=0; i<2; ++i)
			res+=std::max(0,a.d[i]-t[k].Max[i])+std::max(0,t[k].Min[i]-a.d[i]);
		return res;
	}
	int Dis(Point a,Point b){
		return std::abs(a.d[0]-b.d[0])+std::abs(a.d[1]-b.d[1]);
	}
	void Query(Point p,int k)
	{
		Ans=std::min(Ans,Dis(p,t[k].pt));
		int dl=t[k].ls?Dis_node(p,t[k].ls):INF;
		int dr=t[k].rs?Dis_node(p,t[k].rs):INF;
		if(dl<dr){
			if(dl<Ans) Query(p,t[k].ls);
			if(dr<Ans) Query(p,t[k].rs);
		}
		else{
			if(dr<Ans) Query(p,t[k].rs);
			if(dl<Ans) Query(p,t[k].ls);
		}
	}
}
using namespace KD_Tree;

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}

int main()
{
	n=read(),Q=read();
	for(int i=1; i<=n; ++i) p[i].d[0]=read(),p[i].d[1]=read();
	root=Build(1,n,0); Point tmp;
	while(Q--)
		if(read()==1) tmp.d[0]=read(),tmp.d[1]=read(),Insert(tmp,root,0);
		else tmp.d[0]=read(),tmp.d[1]=read(),Ans=INF,Query(tmp,root),printf("%d\n",Ans);

	return 0;
}