BZOJ.3529.[SDOI2014]数表(莫比乌斯反演 树状数组)

题目链接

总感觉博客园的\(Markdown\)很。。\(gouzhi\)，可以看这的。

---

\(Description\)
　　令\(F(i)\)表示\(i\)的约数和，给定\(n,m,a\)，多次询问，求（这个式子博客园Markdown加载不出来 真拉）

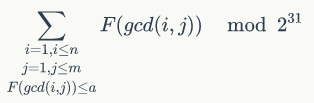
\(Solution\)
　　\(F(i)\)是一个积性函数，根据约数和定理可以线性筛出来。（具体见这，好像比较麻烦，所以直接\(O(n\log n)\)求）

约数和定理：若\(n=p_1^{a_1}p_2^{a_2}\ldots p_k^{a_k}\)，则

\[F(n)=(p_1^0+p_1^1+p_1^2+\ldots+p_1^{a_1})(p_2^0+p_2^1+p_2^2+\ldots+p_2^{a_2})\ldots(p_k^0+p_k^1+p_k^2+\ldots+p_k^{a_k}) \]

　　先考虑去掉\(a\)的限制，

\[\sum_{d=1}^n\sum_{i=1}^n\sum_{j=1}^n[gcd(i,j)=d]*F(d) \]

\[\sum_{d=1}^nF(d)\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{d}\rfloor}[gcd(i,j)=1] \]

\[\sum_{d=1}^nF(d)\sum_{i=1}^{min}\mu(i)\lfloor\frac{n}{id}\rfloor\lfloor\frac{m}{id}\rfloor \]

　　令\(T=id\)，

\[\sum_{d=1}^nF(d)\sum_{d\mid T}\mu(\frac{T}{d})\lfloor\frac{n}{T}\rfloor\lfloor\frac{m}{T}\rfloor \]

　　枚举\(T\)，把\(\lfloor\frac{n}{T}\rfloor\lfloor\frac{m}{T}\rfloor\)放前边，

\[\sum_{T=1}^n\lfloor\frac{n}{T}\rfloor\lfloor\frac{m}{T}\rfloor\sum_{d\mid T}F(d)\mu(\frac{T}{d}) \]

　　前半部分显然可以优化到\(O(\sqrt{n})\)，对于后半部分和之前一样，暴力枚举约数更新，然后求遍前缀和，复杂度\(O(n\log n)\)。
　　然后是\(a\)的限制，因为只有\(F(i)\leq a\)的\(i\)才会对答案有贡献，所以我们将询问按\(a\)排序，\(i\)按\(F(i)\)排序，每次询问将所有\(\leq a\)的\(F(i)\)插入，用树状数组维护前缀和。
　　（详细写一下，原先对于每个\(F(d)\)，我们在预处理时要更新\(d\)的所有倍数的\(\sum F*\mu\)，然后前缀和。现在根据\(F(d)\)的大小依次更新\(d\)的倍数）
　　复杂度\(O(n\log^2n+q\sqrt{n}\log n)\)。

　　另外对于\(2^k\)取模相当于和\(2^k-1\)取"与(&)"。因此对于这题不需要取模，用int自然溢出然后最后答案对\(2^{31}-1\)取与即可。（与0的部分及模掉的部分）
　　注意如果\(k\)不是\(31\)的话，得到的结果应是同余的（即可能是负的）。

---

小结
套路1：由\(\sum_{i=1}^n\sum_{j=1}^n[gcd(i,j)=d]\)，去枚举\(d\)，化简出\(\sum_{d=1}^n\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{d}\rfloor}[gcd(i,j)=1]\)。

套路2：对于\(\sum_{i=1}^{min}\mu(i)\lfloor\frac{n}{id}\rfloor\lfloor\frac{m}{id}\rfloor\)，令\(T=id\)，得到\(\sum_{d\mid T}\mu(\frac{T}{d})\lfloor\frac{n}{T}\rfloor\lfloor\frac{m}{T}\rfloor\)。

套路3：枚举\(T\)，把\(\lfloor\frac{n}{T}\rfloor\lfloor\frac{m}{T}\rfloor\)放前边，后面留下个\(\sum_{d\mid T}^nF(d)\mu(\frac{T}{d})\)。

反正都是满满的套路

---

//2924kb	3464ms
#include <cstdio>
#include <cctype>
#include <algorithm>
#define lb(x) (x)&-(x)
#define gc() getchar()
#define pr std::pair<int,int>
const int N=1e5+5,M=2e4+5,INF=0x7fffffff;

int Q,Max,cnt,P[N>>3],mu[N],Ans[M];
std::pair<int,int> F[N];
bool Not_P[N];
struct Ques{
	int n,m,a,id;
	bool operator <(const Ques x)const{
		return a<x.a;
	}
}q[M];

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}
void Init()
{
	mu[1]=1;
	for(int i=2; i<=Max; ++i)
	{
		if(!Not_P[i]) P[++cnt]=i,mu[i]=-1;//mu[]别漏！
		for(int t,j=1; j<=cnt&&(t=i*P[j])<=Max; ++j)
		{
			Not_P[t]=1;
			if(i%P[j]) mu[t]=-mu[i];
			else {mu[t]=0; break;}
		}
	}
	for(int i=1; i<=Max; ++i)
		for(int j=i; j<=Max; j+=i) F[j].first+=i;
	for(int i=1; i<=Max; ++i) F[i].second=i;
	std::sort(F+1,F+1+Max);
}
namespace BIT
{
	int t[N+3];
	inline void Add(int p,int v){
		while(p<=Max) t[p]+=v,p+=lb(p);
	}
	inline int Query(int p){
		int res=0;
		while(p) res+=t[p],p^=lb(p);
		return res;
	}
	inline int Sum(int l,int r){
		return Query(r)-Query(l-1);
	}
}
int Calc(int n,int m)
{
//	if(n>m) std::swap(n,m);
	int res=0;
	for(int i=1,nxt; i<=n; i=nxt+1)
		nxt=std::min(n/(n/i),m/(m/i)),res+=(n/i)*(m/i)*BIT::Sum(i,nxt);//这不需要*(nxt-i+1)！BIT::Sum就是区间的值。
	return res;
}

int main()
{
	Q=read();
	for(int n,m,i=1; i<=Q; ++i)
	{
		n=read(),m=read(),q[i].a=read(),q[i].id=i;
		if(n>m) std::swap(n,m);
		q[i].n=n, q[i].m=m, Max=std::max(Max,m);
	}
	std::sort(q+1,q+1+Q);
	Init();
	int now=1; F[Max+1].second=INF;
	for(int i=1; i<=Q; ++i){
		for(; F[now].first<=q[i].a; ++now)
			for(int v=0,d=1; (v+=F[now].second)<=Max; ++d)
				BIT::Add(v,F[now].first*mu[d]);
		Ans[q[i].id]=Calc(q[i].n,q[i].m);
	}
	for(int i=1; i<=Q; ++i) printf("%d\n",Ans[i]&INF);

	return 0;
}