洛谷P1886 滑动窗口（POJ.2823 Sliding Window）（区间最值）

To 洛谷.1886 滑动窗口 To POJ.2823 Sliding Window

题目描述

现在有一堆数字共N个数字（N<=10^6），以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is [1 3 -1 -3 5 3 6 7], and k = 3.

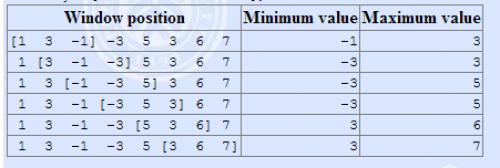
输入输出格式

输入格式：

 

输入一共有两行，第一行为n,k。

第二行为n个数(<INT_MAX).

 

输出格式：

 

输出共两行，第一行为每次窗口滑动的最小值

第二行为每次窗口滑动的最大值

 

输入输出样例

输入样例#1：

8 3
1 3 -1 -3 5 3 6 7

输出样例#1：

-1 -3 -3 -3 3 3
3 3 5 5 6 7

说明

50%的数据，n<=10^5

100%的数据，n<=10^6

代码：

洛谷70分TLE的线段树

#include<cstdio>
#include<algorithm>
using namespace std;
const int N=1000005;

int n,k,From,To,Min[N<<2],Max[N<<2];

void read(int &now)
{
    now=0;int f=1;char c=getchar();
    while(c<'0'||c>'9')
    {
        if(c=='-')f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9')now=now*10+c-'0',c=getchar();
    now*=f;
}

inline void PushUp(int rt)
{
    Min[rt]=min(Min[rt<<1],Min[rt<<1|1]);
    Max[rt]=max(Max[rt<<1],Max[rt<<1|1]);
}

void Build(int l,int r,int rt)
{
    if(l==r)
    {
        int t;
        read(t);
        Min[rt]=Max[rt]=t;
        return;
    }
    int m=(l+r)>>1;
    Build(l,m,rt<<1);
    Build(m+1,r,rt<<1|1);
    PushUp(rt);
}

int QueryMax(int l,int r,int rt,int L,int R)
{
    if(L<=l && r<=R) return Max[rt];
    int m=(l+r)>>1,res=(1<<31);
    if(L<=m) res=max(res,QueryMax(l,m,rt<<1,L,R));
    if(m<R) res=max(res,QueryMax(m+1,r,rt<<1|1,L,R));
    return res;
}

int QueryMin(int l,int r,int rt,int L,int R)
{
    if(L<=l && r<=R) return Min[rt];
    int m=(l+r)>>1,res=(1<<30);
    if(L<=m) res=min(res,QueryMin(l,m,rt<<1,L,R));
    if(m<R) res=min(res,QueryMin(m+1,r,rt<<1|1,L,R));
    return res;
}

int main()
{
    read(n);read(k);
    Build(1,n,1);
    //From=1;To=k;
    for(register int i=1;i<=n-k+1;i++)//,From++,To++
      printf("%d ",QueryMin(1,n,1,i,i+k-1));
    printf("\n");
    //From=1;To=k;
    for(register int i=1;i<=n-k+1;i++)//,From++,To++
      printf("%d ",QueryMax(1,n,1,i,i+k-1));
    return 0;
}

常数优化十分可观的zkw线段树（然而我不会用）

#include<cstdio>
#include<algorithm>
using namespace std;
const int N=1000005;

int n,k,M,Tree[N<<2];

void read(int &now)
{
    now=0;int f=1;char c=getchar();
    while(c>'9'||c<'0')
    {
        if(c=='-')f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9')now=(now<<3)+(now<<1)+c-'0',c=getchar();
    now*=f;
}

void BuildMin(int n)
{
    for(int i=M-1;i;--i)
      Tree[i]=min(Tree[i<<1],Tree[i<<1|1]);
}

void BuildMax(int n)
{
    for(int i=M-1;i;--i)
      Tree[i]=max(Tree[i<<1],Tree[i<<1|1]);
}

int QueryMin(int s,int t,int res)
{
    for(s+=M,t+=M;s^t^1;s>>=1,t>>=1)
    {
        if(~s&1) res=min(res,Tree[s^1]);
        if(t&1) res=min(res,Tree[t^1]);
    }
    return res;
}

int QueryMax(int s,int t,int res)
{
    for(s+=M,t+=M;s^t^1;s>>=1,t>>=1)
    {
        if(~s&1) res=max(res,Tree[s^1]);
        if(t&1) res=max(res,Tree[t^1]);
    }
    return res;
}

int main()
{
    read(n);read(k);
    for(M=1;M<=n+1;M<<=1);
    for(int i=M+1;i<=M+n;i++)
      read(Tree[i]);
    BuildMin(n);
    for(int i=0;i<=n-k;++i)
      printf("%d ",QueryMin(i,i+k+1,1e9));
    printf("\n");
    BuildMax(n);
    for(int i=0;i<=n-k;++i)
      printf("%d ",QueryMax(i,i+k+1,-1e9));
    return 0;
}