博客园 首页 私信博主 显示目录 隐藏目录 管理 动画

洛谷P3373 [模板]线段树 2(区间增减.乘 区间求和)

To 洛谷.3373 [模板]线段树2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.将某区间每一个数乘上x

3.求出某区间每一个数的和

输入输出格式

输入格式：

 

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数乘上k

操作2： 格式：2 x y k 含义：将区间[x,y]内每个数加上k

操作3： 格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

 

输出格式：

 

输出包含若干行整数，即为所有操作3的结果。

 

输入输出样例

输入样例#1：
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4
输出样例#1：
17
2

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^）

样例说明：

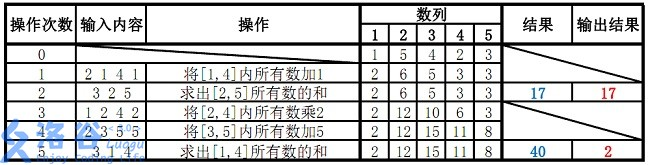
故输出应为17、2（40 mod 38=2）

代码：

  1 #include<cstdio>
  2 #define LL long long//开long long!! 
  3 using namespace std;
  4 const int N=100005;
  5 
  6 int n,m,mod;
  7 LL Sum[N<<2],LazySum[N<<2],LazyMult[N<<2];
  8 
  9 void read(int &now)
 10 {
 11     now=0;int f=1;char c=getchar();
 12     while(c<'0'||c>'9')
 13     {
 14         if(c=='-')f=-1;
 15         c=getchar();
 16     }
 17     while(c>='0'&&c<='9')now=(now<<3)+(now<<1)+c-'0',c=getchar();
 18     now*=f;
 19 }
 20 
 21 void PushUp(int rt)
 22 {
 23     Sum[rt]=Sum[rt<<1]+Sum[rt<<1|1];
 24 }
 25 void PushDown(int rt,int m)
 26 {
 27     if(LazyMult[rt]!=1)//乘法标记需不为1 
 28     {
 29         Sum[rt<<1]*=LazyMult[rt];Sum[rt<<1]%=mod;
 30         Sum[rt<<1|1]*=LazyMult[rt];Sum[rt<<1|1]%=mod;
 31         LazyMult[rt<<1]*=LazyMult[rt];LazyMult[rt<<1]%=mod;
 32         LazyMult[rt<<1|1]*=LazyMult[rt];LazyMult[rt<<1|1]%=mod;
 33         LazySum[rt<<1]*=LazyMult[rt];LazySum[rt<<1]%=mod;
 34         LazySum[rt<<1|1]*=LazyMult[rt];LazySum[rt<<1|1]%=mod;
 35         LazyMult[rt]=1;
 36     }
 37     if(LazySum[rt])
 38     {
 39         Sum[rt<<1]+=LazySum[rt]*(m-(m>>1));Sum[rt<<1]%=mod;
 40         Sum[rt<<1|1]+=LazySum[rt]*(m>>1);Sum[rt<<1|1]%=mod;
 41         LazySum[rt<<1]+=LazySum[rt];LazySum[rt<<1]%=mod;
 42         LazySum[rt<<1|1]+=LazySum[rt];LazySum[rt<<1|1]%=mod;
 43         LazySum[rt]=0;
 44     }
 45 }
 46 void Build(int l,int r,int rt)
 47 {
 48     LazySum[rt]=0;LazyMult[rt]=1;
 49     if(l==r)
 50     {
 51         scanf("%lld",&Sum[rt]);
 52         return;
 53     }
 54     int m=(l+r)>>1;
 55     Build(l,m,rt<<1);
 56     Build(m+1,r,rt<<1|1);
 57     PushUp(rt);
 58 }
 59 void ModifyAdd(int l,int r,int rt,int L,int R,int v)
 60 {
 61     if(L<=l && r<=R)
 62     {
 63         Sum[rt]+=v*(r-l+1);Sum[rt]%=mod;
 64         LazySum[rt]+=v;LazySum[rt]%=mod;
 65         return;
 66     }
 67     PushDown(rt,r-l+1);
 68     int m=(l+r)>>1;
 69     if(L<=m) ModifyAdd(l,m,rt<<1,L,R,v);
 70     if(m<R) ModifyAdd(m+1,r,rt<<1|1,L,R,v);
 71     PushUp(rt);
 72 }
 73 void ModifyMult(int l,int r,int rt,int L,int R,int v)
 74 {
 75     if(L<=l && r<=R)
 76     {//对于懒惰标记 乘法会影响加法，但加法并不会影响乘法 
 77     //所以加法标记必须也乘 
 78         Sum[rt]*=v;Sum[rt]%=mod;
 79         LazySum[rt]*=v;LazySum[rt]%=mod;//更新乘法的同时更新加法 
 80         LazyMult[rt]*=v;LazyMult[rt]%=mod;
 81         return;
 82     }
 83     PushDown(rt,r-l+1);
 84     int m=(l+r)>>1;
 85     if(L<=m) ModifyMult(l,m,rt<<1,L,R,v);
 86     if(m<R) ModifyMult(m+1,r,rt<<1|1,L,R,v);
 87     PushUp(rt);
 88 }
 89 LL QuerySum(int l,int r,int rt,int L,int R)
 90 {
 91     if(L<=l && r<=R) return Sum[rt];
 92     PushDown(rt,r-l+1);
 93     int m=(l+r)>>1;LL res=0;
 94     if(L<=m) res+=QuerySum(l,m,rt<<1,L,R),res%=mod;
 95     if(m<R) res+=QuerySum(m+1,r,rt<<1|1,L,R),res%=mod;
 96     return res;
 97 }
 98 
 99 int main()
100 {
101     read(n);read(m);read(mod);
102     Build(1,n,1);
103     for(int i=1;i<=m;i++)
104     {
105         int opt,a,b;
106         read(opt);read(a);read(b);
107         if(opt==1)
108         {
109             int k;read(k);
110             ModifyMult(1,n,1,a,b,k);
111         }
112         else if(opt==2)
113         {
114             int k;read(k);
115             ModifyAdd(1,n,1,a,b,k);
116         }
117         else
118           printf("%lld\n",QuerySum(1,n,1,a,b));
119     }    
120     return 0;
121 }
posted @ 2017-05-22 17:58  SovietPower  阅读(311)  评论(0)  编辑  收藏  举报