博客园 首页 私信博主 显示目录 隐藏目录 管理 动画

CSAPP Lab4 Cache Lab

目录

CSAPP Lab4 Cache Lab: Understanding Cache Memories

https://www.zybuluo.com/SovietPower/note/1795924
参考：
https://www.jianshu.com/p/e68dd8305e9c

得分测试：

Linux> make
Linux> python driver.py

得分截图：

Part 1

要求：模拟一个组相连高速缓存。只需给出每次操作是否命中、是否发生驱逐即可。

组相连高速缓存有\(S=2^s\)组，每组\(E\)行，每行\(1\)个有效位，\(t\)个标记位，\(B=2^b\)数据位。
地址：\(t\)个标记位，\(s\)个组索引位，\(b\)个块偏移位。
每次模拟即可。

代码还可以优化的地方（但也没必要）：s,b,t,verbose,cache等确实可以定义为局部变量并作为函数参数传递；Cache结构体应有自己的s,b,t，而不是全局的。

测试得分：

Linux> make
linux> ./test-csim

自测：

> csim(.exe) -v -s 4 -E 1 -b 4 -t traces/yi.trace
L 10,1 miss
M 20,1 miss hit
...
M 12,1 miss eviction hit
hits:4 misses:5 evictions:3

代码：

#include "cachelab.h"
#include <stdio.h>
#include <getopt.h>
#include <stdlib.h>
#include <unistd.h>
typedef unsigned long long ull;

const char *Usage="Usage: ./csim-ref [-hv] -s <s> -E <E> -b <b> -t <tracefile>";
const char *Error="Wrong augment.";

typedef struct
{
	int valid, tm;
	ull tag;
}CacheLine; //缓存行 
typedef CacheLine* CacheSet; //缓存组 
typedef CacheSet* Cache; //组相连高速缓存 

int s,S,E,b,B;
int verbose;
int hits=0, misses=0, evictions=0;

Cache cache;
FILE *fp=NULL; //<tracefile>

void Read(int argc, char* argv[])
{
	for(int opt; ~(opt=getopt(argc, argv, "hvs:E:b:t:")); )
	{
		switch(opt)
		{
			case 'h': //Optional help flag that prints usage info
				fprintf(stdout, Usage, argv[0]);
				exit(0);
			case 'v': //Optional verbose flag that displays trace info
				verbose=1;
				break;
			case 's': //Number of set index bits (S = 2^s is the number of sets)
				s=atoi(optarg), S=1<<s;
				break;
			case 'E': //Associativity (number of lines per set)
				E=atoi(optarg);
				break;
			case 'b': //Number of block bits (B = 2^b is the block size)
				b=atoi(optarg), B=1<<b;
				break;
			case 't': //-t <tracefile>: Name of the valgrind trace to replay
				fp=fopen(optarg,"r");
				break;
			default:
				fprintf(stdout, Error, argv[0]);
				exit(1);
		}
	}
}
void Init()
{
	cache=(Cache)malloc(sizeof(CacheSet)*S);
	if(cache==NULL) exit(1);
	for(int i=0; i<S; ++i)
	{
		cache[i]=(CacheSet)calloc(E,sizeof(CacheLine)); //calloc会初始化分配的内容为0，malloc不会 
		if(cache[i]==NULL) exit(1);
	}
}
void Load(int set_id,ull tag)
{
	static int TIME=0;
	++TIME; //time stamp

	int empty=-1, eviction=-1;

	CacheSet set=cache[set_id];
	for(int i=0; i<E; ++i)
	{
		if(set[i].valid)
		{
			if(set[i].tag==tag)
			{
				++hits, set[i].tm=TIME;
				if(verbose) printf(" hit");
				return;
			}
			if(eviction==-1 || set[i].tm<set[eviction].tm)
				eviction=i;
		}
		else empty=i;
	}
	++misses;

	if(~empty)
	{
		set[empty].valid=1, set[empty].tag=tag;
		set[empty].tm=TIME;
		if(verbose) printf(" miss");
	}
	else
	{
		++evictions;
		set[eviction].tag=tag;
		set[eviction].tm=TIME;
		if(verbose) printf(" miss eviction");
	}
}
void Store(int set_id,ull tag)
{
	Load(set_id,tag);
}
void Simulater()
{
	char opt;
	ull add;
	int size;
	while(~fscanf(fp," %c %llx,%d",&opt,&add,&size)) //%I64x
	{
		if(opt=='I') continue;

		int set_id=(add>>b)&(S-1); ull tag=add>>(s+b);
		if(verbose) printf("%c %llx,%d",opt,add,size);
		switch(opt)
		{
			case 'L':
				Load(set_id, tag);
				break;
			case 'S':
				Store(set_id, tag);
				break;
			case 'M':
				Load(set_id, tag), Store(set_id, tag);
				break;
		}
		if(verbose) putchar('\n');
	}
}
// void printSummary(int a,int b,int c)
// {
// 	printf("hits:%d misses:%d evictions:%d\n",a,b,c);
// }

int main(int argc, char* argv[])
{
	Read(argc,argv);
	Init();
	Simulater();
	printSummary(hits,misses,evictions);

	fclose(fp);
	for(int i=0; i<S; ++i) free(cache[i]);
	free(cache); //Always free what you malloc, otherwise may get memory leak

    return 0;
}

Part 2

要求：给定一个\(S=5,E=1,B=5\)的直接映射缓存，即有\(32\)组，每组一行能存\(32\)字节/\(8\)个int。分别对\(32\times 32\)、\(64\times 64\)、\(67\times 61\)的矩阵转置函数做修改，使得其miss数尽量小。
三个函数允许的最大miss数分别为：\(600\)、\(2000\)、\(3000\)，满分为小于\(300\)、\(1300\)、\(2000\)。
此外表现分要求：

  1. 每次最多使用12个局部int变量。
  2. 不能定义数组。
  3. 不能改变A矩阵，但B矩阵可以任意修改。

在trans.c中修改。
若要测试例如\(34\times 12\)的矩阵转置可以使用：
Linux> ./test-trans -M 12 -N 34

自测：

Linux> make
Linux> ./test-trans -M <M> -N <N>

查看错误信息：

Linux> ./tracegen -M 64 -N 64 -F 0

2.1 32×32

做法1

先看一下分组情况：

第一行：\(0\sim 3\)组
第二行：\(4\sim 7\)组
第三行：\(8\sim 11\)组
...
第八行：\(28\sim 31\)组

转置时，A是读同一行，所以miss会很小；而对B需要逐列操作，miss的多少主要取决于B，所以主要关注B。
一般的转置中，B依次写\(1,2,3,...,8,9,10,...,32\)行，依次占用第\(0,4,8,...,28,0,4,...,28\)组。可以发现如果只让B写八行的第一列，再写这八行的下一列直至写完前八列，就不会发生miss/eviction（当然第一列会miss）。
至于A的影响，只是在分块矩阵的主对角线上时，B每写一列（八行）会与A冲突一次，导致两次miss。（注意要先存一下A这行的八个元素，才能写B的这一列，否则A要多miss一次）

结果分析：
对于主对角线上的四个\(8\times 8\)矩阵，miss数为\(2\times 8+7=23\)次；非主对角线上的子矩阵，因为A,B用到的内存组错开了，所以只有\(8+8=16\)次miss。
所以总miss数约为\(23\times 4+16\times 12=284\)，实测\(287\)。

做法2

考虑能否消除做法1中主对角线上，额外的\(7\)次miss。这\(7\)次miss，是因为A,B是 分别按行列 交叉读写的，所以总会有\(7\)次的覆盖。
那么我们A,B全都按行读写，就不会有这\(7\)次覆盖了，每次的一整行都能hit。
注意到缓存可以存下A或B的整个\(8\times 8\)矩阵，不能修改A，但可以修改B。
所以我们把A一行一行赋值给B，是\(16\)次miss；然后再对B的\(8\times 8\)矩阵做转置，额外miss数就是0了（全部在缓存中，全部都hit）。
即先按行复制后整个转置。

这样总miss数为\(16\times 16=256\)，实测\(259\)。

代码：

//Sol1: 287
// for(i=0; i<N; i+=8)
// 	for(j=0; j<M; j+=8)
// 		for(k=i; k<i+8; ++k)
// 		{
// 			v0=A[k][j], v1=A[k][j+1], v2=A[k][j+2], v3=A[k][j+3],
// 			v4=A[k][j+4], v5=A[k][j+5], v6=A[k][j+6], v7=A[k][j+7];
//
// 			B[j][k]=v0, B[j+1][k]=v1, B[j+2][k]=v2, B[j+3][k]=v3,
// 			B[j+4][k]=v4, B[j+5][k]=v5, B[j+6][k]=v6, B[j+7][k]=v7;
// 		}
// return;
//Sol2: 259
for(i=0; i<N; i+=8)
	for(j=0; j<M; j+=8)
	{
		for(k=i, l=j; k<i+8; ++k, ++l)
		{
			v0=A[k][j], v1=A[k][j+1], v2=A[k][j+2], v3=A[k][j+3],
			v4=A[k][j+4], v5=A[k][j+5], v6=A[k][j+6], v7=A[k][j+7];

			B[l][i]=v0, B[l][i+1]=v1, B[l][i+2]=v2, B[l][i+3]=v3,
			B[l][i+4]=v4, B[l][i+5]=v5, B[l][i+6]=v6, B[l][i+7]=v7;
		}
		for(k=0; k<8; ++k)//第j行 第i列（偏移量i,j记得加） 
			for(l=k+1; l<8; ++l)//对于B，行的编号就都加j，列的编号就都加i 
				v0=B[k+j][l+i], B[k+j][l+i]=B[l+j][k+i], B[l+j][k+i]=v0;
	}

2.2 64×64

看一下分组情况：

第一行：\(0\sim 7\)组
第二行：\(8\sim 15\)组
第三行：\(16\sim 23\)组
第四行：\(24\sim 31\)组
第五行：\(0\sim 7\)组...

显然还按\(8\times 8\)分组不利于B的按列写。如果换成\(4\times 4\)分组，B的每列写不会冲突，但缓存中每行的利用率只有一半（能得一点点分）。

考虑综合两种分法，整体采用\(8\times 8\)分组，按行的操作每次处理八个，按列的操作每次处理四个（但注意这四行中的前八列都可以用）。

参考上面链接中的做法及图片：
对每个\(8\times 8\)矩阵，分成四个\(4\times 4\)矩阵，然后做四步：

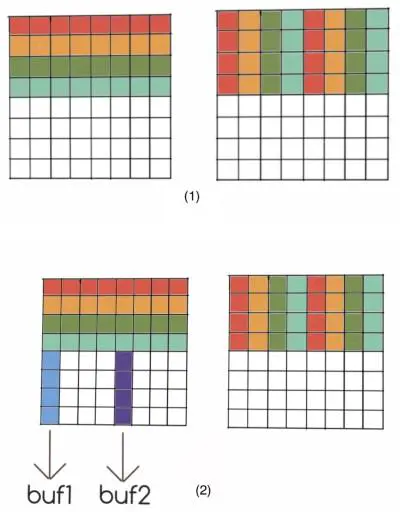
  1. 对A的前四行，前四个数分别存到B的前四列中，后四个数分别存到B的后四列中。
  2. 读A的后四行的第一列、第五列元素，并保存。
  3. 将2.中A的后四行的第一列，放到B当前第一行的后四个元素中（并保存之前这里的四个元素）；将2.中A的后四行的第五列，放到B第五行的后四列去。
  4. 将3.中存下的，原先B第一行的后四个元素，放到B第五行的前四列去。
  5. \(2,3,4\)步对不同列重复做共四次，就可以实现转置了。

这个做法充分利用了，同一行能读\(8\)个数、最多同时存\(4\)整行的性质，以及转置的特点。
总结就是，前四行可以直接按列赋值给B，然后对后四行，左下角部分的每一列放到右上角部分的每一行、右上角的每一行放到左下角部分的每一行、右下角的列转成行位置，就可以实现转置，而且这种方法对内存的利用率很高、miss少。

结果分析：
对于上面的四步，若子矩阵不在主对角线上，则A,B的读写不会相互影响，则：

  1. miss数为\(4+4=8\)。
  2. miss数为\(4\)。
  3. miss数为\(0+1=1\)。
  4. miss数为\(0\)。
  5. 三次重复后的\(2,3,4\)步miss数共\(0+3+0=3\)。

总miss数约为\((8+4+1+3)\times 64=1024\)

若子矩阵在主对角线上，1.中miss数会加\(3\)，每次的3.会多\(4\)（写B的被A驱逐的前四行）+\(3\)（读A的被B驱逐的五六七行）=\(7\)次，所以共多\((3+7)*8=80\)次。

所以总miss数为\(1104\)次，实测\(1107\)次。
1.中多的\(3*8\)次miss可以像2.1中，先复制后转置的方法消除。

代码：

for(i=0; i<N; i+=8)
	for(j=0; j<M; j+=8)
	{
		for(k=i; k<i+4; ++k)
		{
			v0=A[k][j+0], v1=A[k][j+1], v2=A[k][j+2], v3=A[k][j+3],
			v4=A[k][j+4], v5=A[k][j+5], v6=A[k][j+6], v7=A[k][j+7];

			B[j][k]=v0, B[j+1][k]=v1, B[j+2][k]=v2, B[j+3][k]=v3,
			B[j][k+4]=v4, B[j+1][k+4]=v5, B[j+2][k+4]=v6, B[j+3][k+4]=v7;
		}
		for(k=j; k<j+4; ++k)
		{
			v0=A[i+4][k], v4=A[i+4][k+4],
			v1=A[i+5][k], v5=A[i+5][k+4],
			v2=A[i+6][k], v6=A[i+6][k+4],
			v3=A[i+7][k], v7=A[i+7][k+4],

			tmp=B[k][i+4], B[k][i+4]=v0, v0=tmp;
			tmp=B[k][i+5], B[k][i+5]=v1, v1=tmp;
			tmp=B[k][i+6], B[k][i+6]=v2, v2=tmp;
			tmp=B[k][i+7], B[k][i+7]=v3, v3=tmp;

			B[k+4][i+0]=v0, B[k+4][i+1]=v1, B[k+4][i+2]=v2, B[k+4][i+3]=v3,
			B[k+4][i+4]=v4, B[k+4][i+5]=v5, B[k+4][i+6]=v6, B[k+4][i+7]=v7;
		}
	}

2.3 67×61

类似2.1，每行是\(61\)个，所以依旧利用Cache能存B的\(8\)行的性质，对B每\(8\)行处理一次，每次处理所有行的这八个元素的A->B赋值。
因为限制为\(2000\)足够大，比较容易过。实测\(1761\)。
不过\(16\times 16\)分块，暴力转置也能恰好不超过\(2000\)。

代码：

for(j=0; j<56; j+=8)
	for(i=0; i<67; ++i)
	{
		v0=A[i][j], v1=A[i][j+1], v2=A[i][j+2], v3=A[i][j+3],
		v4=A[i][j+4], v5=A[i][j+5], v6=A[i][j+6], v7=A[i][j+7];

		B[j][i]=v0, B[j+1][i]=v1, B[j+2][i]=v2, B[j+3][i]=v3,
		B[j+4][i]=v4, B[j+5][i]=v5, B[j+6][i]=v6, B[j+7][i]=v7;
	}
for(i=0; i<64; ++i)//右上 
	for(j=56; j<61; ++j)
		B[j][i]=A[i][j];
for(i=64; i<67; ++i)//右下 
	for(j=56; j<61; ++j)
		B[j][i]=A[i][j];
posted @ 2021-05-23 01:10  SovietPower  阅读(452)  评论(0)  编辑  收藏  举报