BZOJ.3227.[SDOI2008]红黑树tree(树形DP 思路)

BZOJ
洛谷

orz MilkyWay天天做sxt！

---

首先可以树形DP：\(f[i][j][0/1]\)表示\(i\)个点的子树中，黑高度为\(j\)，根节点为红/黑节点的最小红节点数（最大同理）。
转移的时候枚举两棵子树中有多少点、颜色是什么即可。
因为红黑树的深度是\(O(\log n)\)的，所以第二维只需要\(O(\log n)\)，所以复杂度是\(O(n^2\log n)\)。代码这里有。

---

因为问题可以拆分成子问题，所以我们考虑几种节点数较少的子树的情况，然后把这棵子树合并成一个黑点（表示一棵以该黑点为根的子树）。
对于两个黑点，我们可以把它合并成一个黑点。
对于三个黑点，可以合并成一个红点与一个黑点。
对于四个黑点，可以合并成两个红点与一个黑点。
（看图就很好理解了，盗用一下这位dalao的图）

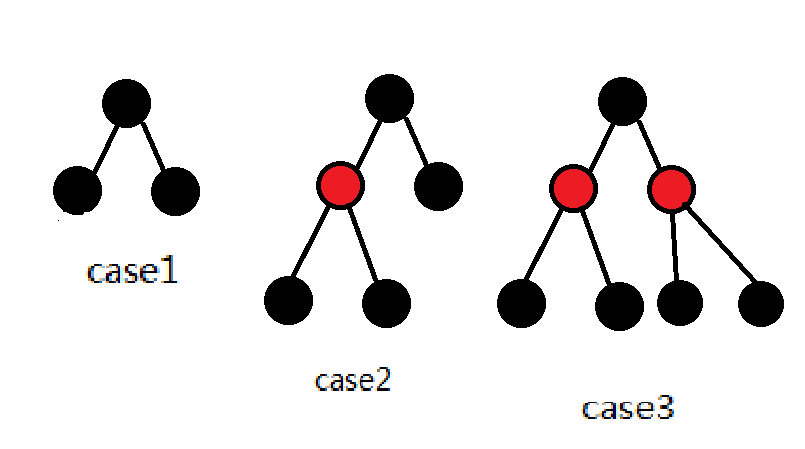
而且只需要考虑这三种情况。

初始的时候前端节点有\(n+1\)个，所以相当于把\(n+1\)个黑点合并至\(1\)个点。
大概也可以这么理解：因为将\(x\)个黑点合并成一个黑点，本质上就是确定\(x-1\)个点选什么颜色。所以我们合并\(n+1\)个点就可以了。
求最小值就每次合并\(2\)个，当有奇数时是\(3\)个点，得补一个红点。
求最大值就每次合并\(4\)个。因为实际上就是每次填\(1\)的深度，所以如果多余\(1\)个要与一个\(4\)拼成\(2\)和\(3\)，余下\(2\)个或\(3\)个可以直接单独合并成\(1\)个。最后剩下两个的时候特判下，根节点可以放红点。

另外这样高度限制没有问题，刚开始是一层高度相同的前端节点，然后两个两个合并，高度都会\(+1\)（多出来就合并3个，高度也是\(+1\)）。
四个四个合并同理。

---

//820kb	0ms
#include <cstdio>

int main()
{
	int n,ans=0; scanf("%d",&n);
	for(int x=n+1; x>1; x>>=1) ans+=x&1;
	printf("%d\n",ans), ans=0;
	for(int x=n+1; x>1; )
	{
		if(x==2) ++ans; 
		switch(x&3)
		{
			case 0: ans+=x>>1, x>>=2; break;// /4*2
			case 1: ans+=(x>>1)-1, x>>=2, ++x; break;// /4*2-1
			case 2: ans+=(x>>2)<<1, x>>=2, ++x; break;
			case 3: ans+=((x>>2)<<1)+1, x>>=2, ++x; break;
		}
	}
	printf("%d\n",ans);

	return 0;
}