BZOJ.3648.寝室管理(点分治 树状数组)

BZOJ

---

\(Description\)
求在一棵树上加一条边后，有多少条至少有\(k\)个点的路径。
\(n\leq10^5\)。

---

\(Solution\)
对于一棵树的情况，可以点分治。
用树状数组维护有\(x\)个点的路径有多少条。处理子树时先用子树中的路径统计一下答案，然后再用子树更新一下树状数组。这样求出的路径就是不同子树之间的了。
也可以用容斥的写法，把所有子树的路径长度统计出来然后sort，双指针维护下。
这两个都是\(O(n\log^2n)\)的。
也可以直接用后缀和维护。只要每次复杂度都是当前子树的最大深度，复杂度就是\(O(n\log n)\)。（因为是维护后缀和其实不用把子树按最大深度排序）

表示刚知道树状数组能维护后缀和QAQ（MilkyWay太强啦）

---

对于多出来的一条边，考虑经过这条边的路径的贡献。我们可以枚举环上的边作为分界，去计算分隔后两部分的点之间的路径。（看代码还是很好理解的）
详细点是这样的：

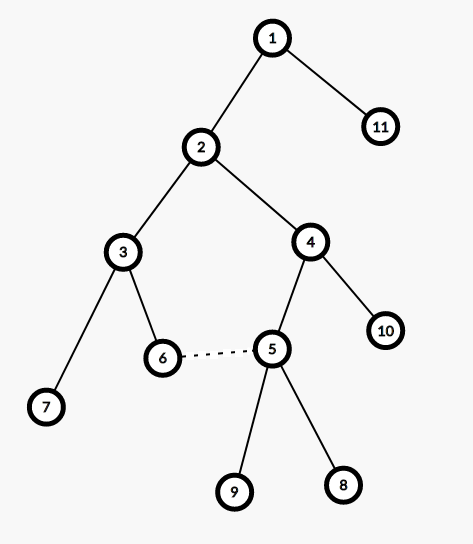
图中的环是：\(6-5-4-2-3-6\)
依次删掉环上除了\(6-5\)的边，看怎么计算答案。

删掉\(4-5\)的时候，答案就是，断开\(4-5\)后\(6\)能到的点，也就是\(6\)到除了\(5\)子树外的各个子树中的路径，与，断开\(4-5\)后\(5\)能到的点，也就是\(5\)到\(5\)子树内的路径，两两组合出来的答案。
答案和点分治的时候一样，用树状数组计算。
然后这样枚举环上每条边，统计答案。

所以我们可以这样：
先从\(6\)开始DFS，对于DFS到的每个点\(x\)，将\(dis(6,x)\)加到树状数组上。
然后按\(5-4-2-3\)的顺序依次枚举环上的点\(s\)，删掉\(s\)的子树在树状数组里的贡献，然后DFS \(s\)的子树。对DFS到的每个点\(x\)，查树状数组中有多少条路径能和\(dis(s,x)\)组成\(\geq k\)的路径，加到答案里。

这样枚举一圈环上的点，每次删掉它子树的贡献然后用它子树内的点统计一次答案，就可以啦。

---

为什么怎么卡都卡不过MilkyWay啊。。orzorz！
我怎么卡不到6666kb啊（当然卡不到了）

---

树状数组：

//6276kb	2132ms
#include <cstdio>
#include <cctype>
#include <algorithm>
//#define gc() getchar()
#define MAXIN 300000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
typedef long long LL;
const int N=1e5+5;

int K,fa[N],Enum,H[N],nxt[N<<1],to[N<<1],Min,root,sz[N],dis[N];
bool vis[N],tag[N];
LL Ans;
char IN[MAXIN],*SS=IN,*TT=IN;
struct BIT
{
	int n,t[N];
	#define lb(x) (x&-x)
	inline void Add(int p)
	{
		for(n=std::max(n,p); p; p^=lb(p)) ++t[p];
	}
	inline void Subd(int p)
	{
		for(; p; p^=lb(p)) --t[p];
	}
	inline void Clear()
	{
		for(int p=n; p; --p) t[p]=0;
	}
	inline int Query(int p)
	{
		int res=0;
		for(p=std::max(p,1); p<=n; p+=lb(p)) res+=t[p];
		return res;
	}
}T;

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-48,c=gc());
	return now;
}
inline int Find(int x)
{
	return x==fa[x]?x:fa[x]=Find(fa[x]);
}
inline void AE(int u,int v)
{
	to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum;
	to[++Enum]=u, nxt[Enum]=H[v], H[v]=Enum;
}
void FindRoot(int x,int fa,int tot)
{
	int mx=0; sz[x]=1;
	for(int i=H[x],v; i; i=nxt[i])
		if(!vis[v=to[i]] && v!=fa)
			FindRoot(v,x,tot), sz[x]+=sz[v], sz[v]>mx&&(mx=sz[v]);
	mx=std::max(mx,tot-sz[x]);
	if(mx<Min) Min=mx, root=x;
}
void Calc1(int x,int fa,int dep)
{
	Ans+=T.Query(K-dep);
	for(int i=H[x]; i; i=nxt[i])
		if(!vis[to[i]] && to[i]!=fa) Calc1(to[i],x,dep+1);
}
void Upd1(int x,int fa,int dep)//应该在Calc时用vector存一下dep，DFS常数大s 
{
	T.Add(dep);
	for(int i=H[x]; i; i=nxt[i])
		if(!vis[to[i]] && to[i]!=fa) Upd1(to[i],x,dep+1);
}
void Solve1(int x)
{
	vis[x]=1, T.n=0, T.Add(1);
	for(int i=H[x],v; i; i=nxt[i])
		if(!vis[v=to[i]]) Calc1(v,x,1), Upd1(v,x,2);//点数>=K 
	T.Clear();
	for(int i=H[x],v; i; i=nxt[i])
		if(!vis[v=to[i]]) Min=N, FindRoot(v,x,sz[v]), Solve1(root);
}
void Clear2(int x,int fa)
{
	T.Subd(dis[x]);
	for(int i=H[x]; i; i=nxt[i])
		if(!tag[to[i]] && to[i]!=fa) Clear2(to[i],x);
}
void Calc2(int x,int fa,int dep)
{
	Ans+=T.Query(K-dep);
	for(int i=H[x]; i; i=nxt[i])
		if(!tag[to[i]] && to[i]!=fa) Calc2(to[i],x,dep+1);//Calc2!!
}
void Solve2(int x)
{
	T.Add(dis[x]=dis[fa[x]]+1);
	for(int i=H[x]; i; i=nxt[i])
		if(to[i]!=fa[x]) fa[to[i]]=x, Solve2(to[i]);
}

int main()
{
	static int path[N];
	const int n=read(),m=read(); K=read();
	for(int i=1; i<=n; ++i) fa[i]=i;
	int s=0,t=0;
	for(int i=1,u,v; i<=m; ++i)
		if(Find(u=read())!=Find(v=read())) fa[fa[u]]=fa[v], AE(u,v);
		else s=u, t=v;
	Min=N, FindRoot(1,1,n), Solve1(root);
	if(s)
	{
		T.n=0, fa[s]=0, Solve2(s);//此时s为根节点 
		int cnt=0;
		for(int x=t; x; x=fa[x]) tag[path[++cnt]=x]=1;
		for(int i=1; i<cnt; ++i) Clear2(path[i],0), Calc2(path[i],0,i);
	}
	printf("%lld\n",Ans);

	return 0;
}

---

直接后缀和：

//7056kb	1740ms
#include <cstdio>
#include <cctype>
#include <algorithm>
//#define gc() getchar()
#define MAXIN 300000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
typedef long long LL;
const int N=1e5+5;

int K,fa[N],Enum,H[N],nxt[N<<1],to[N<<1],Min,root,sz[N],dis[N],mxdep,f[N],g[N];
bool vis[N],tag[N];
LL Ans;
char IN[MAXIN],*SS=IN,*TT=IN;
struct BIT
{
	int n,t[N];
	#define lb(x) (x&-x)
	inline void Add(int p)
	{
		for(n=std::max(n,p); p; p^=lb(p)) ++t[p];
	}
	inline void Subd(int p)
	{
		for(; p; p^=lb(p)) --t[p];
	}
	inline int Query(int p)
	{
		int res=0;
		for(p=std::max(p,1); p<=n; p+=lb(p)) res+=t[p];
		return res;
	}
}T;

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-48,c=gc());
	return now;
}
inline int Find(int x)
{
	return x==fa[x]?x:fa[x]=Find(fa[x]);
}
inline void AE(int u,int v)
{
	to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum;
	to[++Enum]=u, nxt[Enum]=H[v], H[v]=Enum;
}
void FindRoot(int x,int fa,int tot)
{
	int mx=0; sz[x]=1;
	for(int i=H[x],v; i; i=nxt[i])
		if(!vis[v=to[i]] && v!=fa)
			FindRoot(v,x,tot), sz[x]+=sz[v], sz[v]>mx&&(mx=sz[v]);
	mx=std::max(mx,tot-sz[x]);
	if(mx<Min) Min=mx, root=x;
}
void Calc1(int x,int fa,int dep)
{
	++g[dep], mxdep=std::max(dep,mxdep), Ans+=f[std::max(K-dep-1,0)];//更新的时候还是用d更新吧 这样查询的是k-dep-1。
	for(int i=H[x]; i; i=nxt[i])
		if(!vis[to[i]] && to[i]!=fa) Calc1(to[i],x,dep+1);
}
void Solve1(int x)
{
	vis[x]=1; int mx=0; f[0]=1;
	for(int i=H[x]; i; i=nxt[i])
		if(!vis[to[i]])
		{
			mxdep=0, Calc1(to[i],x,1);
			for(int j=mxdep; j; --j) g[j-1]+=g[j], f[j]+=g[j], g[j]=0;
			f[0]+=g[0], g[0]=0;
			mx=std::max(mx,mxdep);
		}
	for(int i=0; i<=mx; ++i) f[i]=0;
	for(int i=H[x],v; i; i=nxt[i])
		if(!vis[v=to[i]]) Min=N, FindRoot(v,x,sz[v]), Solve1(root);
}
void Clear2(int x,int fa)
{
	T.Subd(dis[x]);
	for(int i=H[x]; i; i=nxt[i])
		if(!tag[to[i]] && to[i]!=fa) Clear2(to[i],x);
}
void Calc2(int x,int fa,int dep)
{
	Ans+=T.Query(K-dep);
	for(int i=H[x]; i; i=nxt[i])
		if(!tag[to[i]] && to[i]!=fa) Calc2(to[i],x,dep+1);//Calc2!!
}
void Solve2(int x)
{
	T.Add(dis[x]=dis[fa[x]]+1);
	for(int i=H[x]; i; i=nxt[i])
		if(to[i]!=fa[x]) fa[to[i]]=x, Solve2(to[i]);
}

int main()
{
	static int path[N];
	const int n=read(),m=read(); K=read();
	for(int i=1; i<=n; ++i) fa[i]=i;
	int s=0,t=0;
	for(int i=1,u,v; i<=m; ++i)
		if(Find(u=read())!=Find(v=read())) fa[fa[u]]=fa[v], AE(u,v);
		else s=u, t=v;
	Min=N, FindRoot(1,1,n), Solve1(root);
	if(s)
	{
		T.n=0, fa[s]=0, Solve2(s);
		int cnt=0;
		for(int x=t; x; x=fa[x]) tag[path[++cnt]=x]=1;
		for(int i=1; i<cnt; ++i) Clear2(path[i],0), Calc2(path[i],0,i);
	}
	printf("%lld\n",Ans);

	return 0;
}