BZOJ.4910.[SDOI2017]苹果树(树形依赖背包 DP 单调队列)

BZOJ
洛谷

\(shadowice\)已经把他的思路说的很清楚了，可以先看一下会更好理解？
这篇主要是对\(Claris\)题解的简单说明。与\(shadowice\)的做法还是有差异的（比如并没有明显用到后序遍历的性质），而且用这种写法可能跑的比较轻松？
（另外你只要想明白\(f,h\)是代表啥，就很好理解了...）

问题等价于树形依赖背包，允许一条链每个点各免费取一次。

免费取一条链即\(t\leq h+k\)的限制。这样最优解一定会免费取了一条从叶子到根节点的链。

现在考虑一下怎么做。不妨枚举这条链（也就是枚举叶子）。
假如我们枚举的叶子是7，也就是这样：

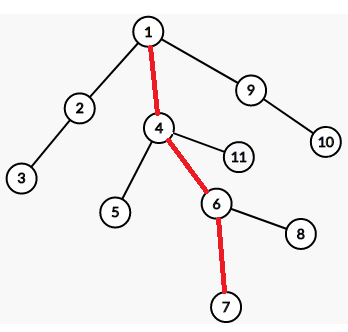
同样我们可以考虑这么4部分：
\((1)\) \(1-4-6-7\)这条链可以免费取一次
\((2)\) \(1-4-6-7\)这条链还可以付费取\(a_i-1\)次
\((3)\) 链左边的点可以各付费取\(a_i\)次
\((4)\) 链右边的点可以各付费取\(a_i\)次

\((1)\)只需要在叶子处算一下到根节点路径上的权值和就可以了（就是\(val_1+val_4+val_6+val_7\)）。
\((2)\)就是对当前链做多重背包（不过每个物品的个数为\(a_i-1\)）。
\((3)\)是对前边枚举过的非链上的点做背包。如果把邻接表反过来，\((4)\)和\((3)\)的求法是一样的（也是对前面的点背包）。

单是枚举叶子就是\(O(n)\)的了。所以我们八成需要DP预处理每个叶子处\((2)(3)(4)\)三个值。
不妨DP的时候将\((2)(3)\)合并到一起算，\((4)\)在反转边表后再计算。

---

设\(f[i][j]\)表示按DFS序考虑到\(i\)，体积为\(j\)的最大收益。

\(f[i][j]\)就是到\(i\)节点，已用体积为\(j\)，同时考虑了\((2)(3)\)两种情况的最大值（只考虑了当前点到根节点的链和链左边的点）。
比如\(f[7][j]\)就是对\(2,3,5,1,4,6,7\)做完多重背包，已用体积为\(j\)的最大价值（背包时\(1,4,6,7\)的个数分别都是\(a_i-1\)）。

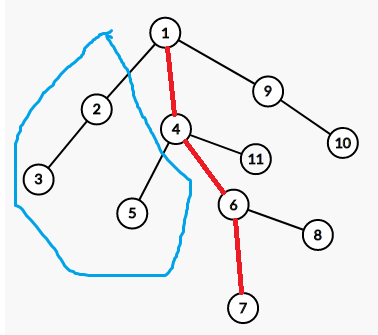
怎么求呢？可以先看一下\(Claris\)的代码。

先放入不能免费的物品，等遍历完儿子后再放入必选的物品，那么\(i\)到根路径上所有点都只算了不能免费的部分。

举个例子：从\(4\)访问完\(5\)子树后，然后访问\(6\)，显然\(f[6]\)就是\(f[5]\)再加入\(1\)个\(5\)和\(a_6-1\)个\(6\)做一次多次背包（\(5\)此时就不能免费取了，因为之前是免费且必选的所以并没有计算；而\(6\)此时会免费取一次，最后加到链上就可以了，所以此时计算\(a_6-1\)个，即不能免费的）。
当然我们不能直接去修改\(f[5]\)这个数组，但我们可以更新数组\(f[4]\)，因为它不是叶子，最后就用不到它的\(f\)值。而且\(4\)的其它儿子比如\(11\)，也可以直接用\(f[4]\)更新它。

也就是我们要用\(f[5]\)和\(1个5\)更新\(f[4]\)，即\(f[4][j]=\max\{f[4][j],\ f[5][j-1]+val_5\}\)。
注意此时\(f[5][j]\)是考虑过\(5\)子树内的，不能直接用\(f[5][j]\)转移（可能一个\(5\)也没有选），要强制选一个\(5\)再转移。
然后用\(f[4]\)更新\(f[6]\)。其实就是先把\(f[4]\)复制给\(f[6]\)，然后用\(f[6]\)和\(a_6-1\)个\(6\)做多重背包。

那么算法流程大概是：记\(v\)的父节点为\(x\)，先把\(f[x]\)复制给\(f[v]\)，然后用\(a_v-1\)个\(v\)更新\(f[v]\)，递归到\(v\)。处理完\(v\)子树后，再用\(f[v]\)加入一个\(v\)做背包来更新\(f[x]\)，以便更新后面的子节点。

这里对\(f[i]\)做多重背包是\(f[i][j]=\max_{k=1}^{a_i-1}\{f[i][j-k]+k*val_i\}\)，可以用单调队列维护，\(O(k)\)更新。

---

然后将DFS序翻转，设\(h[i][j]\)表示按DFS序考虑到\(i\)，体积为\(j\)的最大收益。

\(h[i][j]\)表示到节点\(i\)，已用体积\(j\)，情况\((4)\)的最大价值，也就是只考虑它到根节点的链的右边的点的最大价值。
比如\(h[7]\)，就是对\(9,10,11,8\)做多重背包后的dp数组：

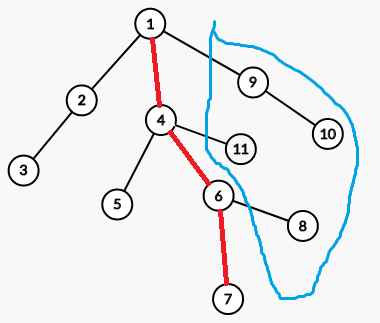
等遍历完儿子后再放入必选的物品和不能免费的物品，那么\(i\)到根路径上所有点都没有算。

转移方式与\(f\)很类似，只是需要在遍历完\(i\)的子树后，才用\(a_i,val_i\)更新\(h[i]\)（这样在用\(h[i]\)更新子树时并没有计算当前链上的，只考虑了链右边的点）。不细说了。（和后序遍历也挺类似的？）

---

如此一来，对于每个叶子\(i\)，用 \(f[i][j]+h[i][k-j]+免费取一次到根节点的路径的权值\) 更新答案即可。
对于不能免费的物品，需要用单调队列优化转移。
时间复杂度\(O(nk)\)。

---

细节：
二维数组最好用一维数组代替（注意每个点的空间是\(k+1\)）。
其它注意一下就好了。

背包也能出成这样orz。

---

//204792kb	33008ms
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
//#define gc() getchar()
#define MAXIN 300000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
typedef long long LL;
const int N=20005,MAXK=5e5+5,M=25000005+N+MAXK;

int n,m,K,Sz,Ans,A[N],val[N],fa[N],Enum,H[N],nxt[N],F[M],G[M];
char IN[MAXIN],*SS=IN,*TT=IN;

inline int read()
{
	int now=0;register char c=gc();
	for(;!isdigit(c);c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now;
}
#define AE(u,v) nxt[v]=H[u], H[u]=v//只需要to且是单向边就用不着了to[]啊 
void Calc(int *f,int A,int val)
{
	static int v[MAXK],q[MAXK];
	for(int i=0,s=0,h=1,t=0,tmp; i<=m; ++i,s+=val)
	{
		tmp=f[i]-s;
		while(h<=t && tmp>v[t]) --t;
		q[++t]=i, v[t]=tmp;
		while(i-q[h]>A) ++h;
		f[i]=v[h]+s;
	}
}
void DFS1(int x)
{
	int *Fx=F+x*K;
	if(A[x]) Calc(Fx,A[x],val[x]);
	for(int v=H[x]; v; v=nxt[v])
	{
		memcpy(F+v*K,Fx,Sz);
		DFS1(v);
		int *fx=Fx+1,*fv=F+v*K,val=::val[v];//f[x][j]=max(f[x][j],f[v][j-1]+val[v])
		for(int j=1; j<=m; ++j,++fx,++fv) *fx=std::max(*fx,*fv+val);
	}
}
void DFS2(int x,int sum)
{
	int *Gx=G+x*K;
	for(int v=H[x]; v; v=nxt[v])
	{
		memcpy(G+v*K,Gx,Sz);
		DFS2(v,sum+val[v]);
		int *gx=Gx+1,*gv=G+v*K,val=::val[v];//从v这棵子树中转移要强制至少选一个v 
		for(int j=1; j<=m; ++j,++gx,++gv) *gx=std::max(*gx,*gv+val);
	}
	if(!H[x])
	{
		int *Fx=F+x*K,*Gx=G+x*K+m,ans=0;
		for(int i=0; i<=m; ++i,++Fx,--Gx) ans=std::max(ans,*Fx+*Gx);
		Ans=std::max(Ans,ans+sum);
	}
	if(A[x]) Calc(Gx,A[x],val[x]);
}

int main()
{
	for(int T=read(); T--; )
	{
		n=read(),m=read(),K=m+1,Sz=K<<2;//m+1!
		memset(H,0,n+1<<2), memset(F,0,Sz), memset(G,0,Sz);
		for(int i=1; i<=n; ++i)
		{
			if((fa[i]=read())) AE(fa[i],i);
			A[i]=read()-1, val[i]=read();
		}
		DFS1(1);
		memset(H,0,n+1<<2);
		for(int i=n; i>1; --i) AE(fa[i],i);
		Ans=0, DFS2(1,val[1]);
		printf("%d\n",Ans);
	}
	return 0;
}