P3985 不开心的金明
1.求出最长好子序列 I
2.P3985 不开心的金明
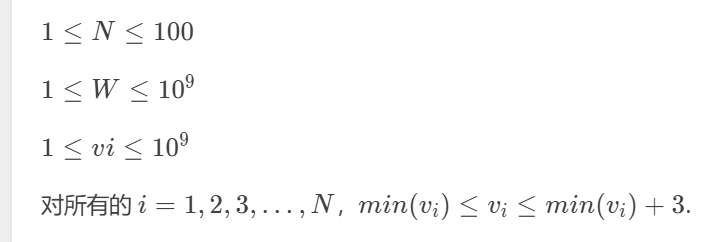
题目看起来很像01背包,也就是dp【i】【j】表示前i个物品,花费为j,最多价值为dp【i】【j】
注意到题中给的数据范围,如果用常规01背包状态转移,有下面的问题:
v很大,花费很大,也就是说没法开这么大的二维数组,但是我们注意到
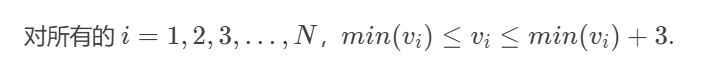
这意味着我们可以让所有的价格都减去最小的价格,这样价格的范围就变为【0,3】,这样以后再用01背包,最后把价格加回去判断就好了。就可以用二维数组存储价格了。
但是如果我们减完最小值,直接01背包,会发现,这是没法实现的。因为最后判断价格的时候,我们只知道遍历过了i个物品,但不知道我们选中了几个物品。没法通过把最小价格加回去计算真正的价格。
所以我们需要更改01背包的状态
原先的状态 dp【i】【j】表示前i个物品,花费为j,最多价值为dp【i】【j】
现在需要的状态 dp【i】【j】【k】 表示前i个物品中,选j个物品(很重要),价值为k(已减去j*min)
转移方程为 dp[i][j][k] = max(dp[i-1][j][k],dp[i-1][j-1][k-v[i]]+p[i]);
code
int v[N],p[N];
int dp[110][110][310];
void solve()
{
cin>>n>>w;
int mi = 1e9+10;
rep(i,1,n)
{
cin>>v[i]>>p[i];
mi = min(mi,v[i]);
}
rep(i,1,n) v[i] -= mi;
rep(i,1,n)
{
rep(j,1,i)
{
rep(k,0,300)
{
dp[i][j][k] = dp[i-1][j][k];
if(k>=v[i]) dp[i][j][k] = max(dp[i][j][k],dp[i-1][j-1][k-v[i]]+p[i]);
}
}
}
int ans = 0;
rep(i,1,n)
{
rep(j,0,300)
{
if(i*mi+j<=w) ans = max(ans,dp[n][i][j]);
}
}
cout<<ans<<endl;
}




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· 25岁的心里话