基于神经网络的函数逼近

I任务要求

1.1求解函数逼近问题

　　有21组单输入矢量和相对应的目标矢量,试设计神经网络来实现这对数组的函数关系

　　P = -1 : 0.1 : 1

　　T=[ -0.96  -0.577  -0.0729  0.377  0.641  0.66  0.461  0.1336

　　　　-0.201   -0.434  -0.5   -0.393  -0.1647  0.0988  0.3072

　　　　0.396  0.3449  0.1816  -0.0312  -0.2183  -0.3201]

　　测试集

　　P2= -1 : 0.025 : 1

II BP神经网络

2.1 神经网络

　　神经网络是模拟人脑生物过程的具有人工智能的系统，是由大量非线性处理单元连接而成的网络，具有高度非线性等特点，可以根据给定的学习样本，不需要进行任何假设，建立系统的非线性输入、输出映射关系。神经网络具有自学习、容错能力强、并行计算等许多优点，被广泛应用于线性系统的建模。

　　神经网络模型可以分为前馈网络、反馈网络、自组织网络和混合神经网络。其中，前馈网络的神经元分层排列，有输入层、隐含层和输出层，每一层神经元只接受前一层的输入，并输出到下一层，网络中没有反馈，实现信号从输入空间到输出空间的变换，其信息处理能力来源于简单非线性函数的多次复合。这种结构的网络通畅比较适合预测、模式识别、非线性函数的逼近等，误差反向传播（BP）网络、线性网络和径向基函数（RBF）网络就属于此类网络。^[1]

2.2 BP网络

　　前馈网络中获得最广泛应用的是BP网络，它是一种单向传播的多层前馈网络，网络除输入、输出层节点外，还包括一层或多层隐含层节点，每一层节点的输出只影响下一层节点的输入。BP网络主要用于系统辨识、模式识别、图像处理、函数逼近、优化计算、最优预测和自适应控制等领域。

2.2.1 BP网络模型

　　BP网络是一种多层前馈神经网络，包括输入层，隐层(中间层)和输出层，其中 隐层可以是一层也可以是多层，一般而言，三层BP神经网络就可以解决大部分比较简单的问题。BP网络前后层之间实现全连接，每层神经元之间无连接。

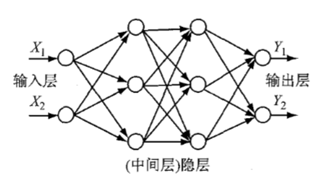
图1 BP神经网络图

　　图 1所示为一个四层 BP网络 ，其中隐层(中间层)为两层，隐层的神经元个数为3个，输入层、输出层的神经元个数均为 2个。学习样本给了BP网络后，各神经元响应输入，信号从输入层，经隐层(中间层)，向输出层传播，根据减少预期输出与实际输出差距这一原则，从输出层，经过各中间层，最后回到输入层 ， 逐层修正各个连接权值 ，这种算法被称为 “误差逆传播算法”，简称BP算法，随着误差逆传播的不断进行网络响应输入的正确率也不断上升。

2.2.2算法过程

 　　BP算法的过程大致如下 ：

　　（1）将各权值、阈值置为小的随机数；

　　（2）从训练数据中挑选一组数据（），将输入数据X加到BP神经网络的输入层，T为预期输出数据，上标K为训练数据号；

　　（3）由计算从第一层直至输出层各节点j的输出，其中上标m为BP网络的层标号，F为神经元的激励函数，为BP网络m-1层的i节点的输出，为M-1层的i节点到m层的j节点的连接权值，M=M,M-1，···,1。

 

 

2.2.3 基于BP神经网络的函数逼近

　　（1）隐层神经元数目的选择需要经验和多次试验来确定，隐层神经元的数目与问题的复杂程度、输入输出神经元的数目都有关系，隐层神经元太多会导致网络结构复杂，学习时间长等问题。

　　（2）传递函数的选择十分重要，BP神经网络的传递函数是处处可微的，常用的传递函数有Sigmoid型的对数函数、正切函数和线性函数。

　　（3）训练函数对BP网络的性能也有影响，可分为普通训练函数和快速训练函数。普通训练函数主要有两种，一种是批梯度下降训练函数（traind），另一种是动量批梯度下降训练函数（traingdm）。前者是根据批梯度下降算法，沿网络性能参数的负梯度方向去调节BP神经网络的权值和阈值，后者是引入一个动量项，每次BP网络权值和阈值改变量中加入前一次的改变量。快速训练函数分自适应修改学习率算法、弹回的BP算法、共轭梯度算法等。

III 函数逼近MATLAB实现

3.1 运行程序

　　当输入为P = -1 : 0.1 : 1时，MATLAB代码^[3]为：

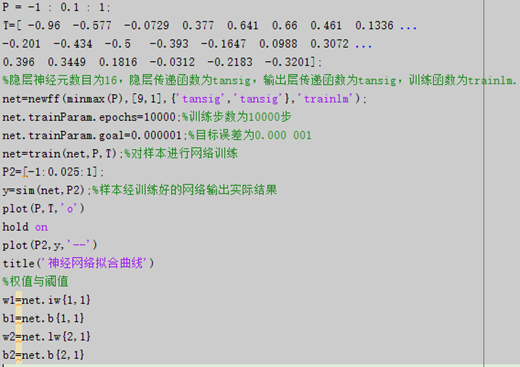
　　通过改变n的值、更换传递函数和训练函数等可以得到不同的拟合效果。

3.2 运行结果

　　最佳运行选择函数：隐层传递函数为tansig，输出层传递函数为tansig，训练函数为trainglm，隐层神经元数目为1~16时，最佳拟合效果如下：

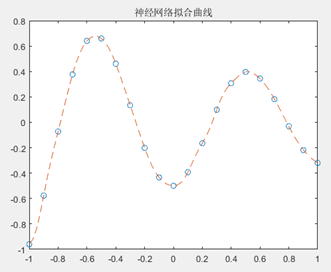
图2 神经网络函数逼近拟合曲线

3.3 结果分析

3.3.1 隐层神经元数目分析

　　当采用同样的传递函数和训练函数时，隐层神经元数目不同导致结果不同，

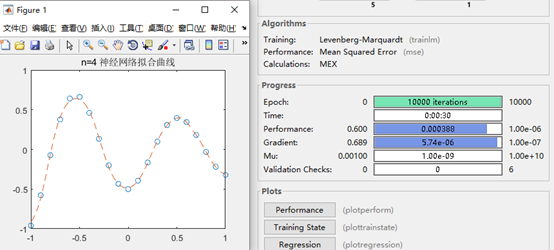
图3 n=4时神经网络运行状态及结果

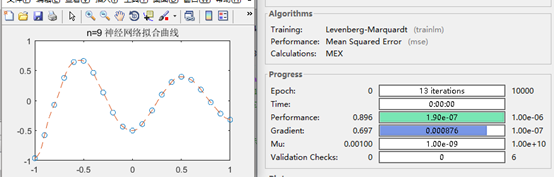
图4 n=9时神经网络运行状态及结果

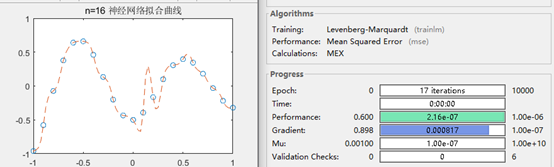
图5  n=16时神经网络运行状态及结果

　　可见，当N=8/9是最合适的，网络结构相对简单，收敛速度也快，拟合效果较佳。

3.3.2 训练函数分析

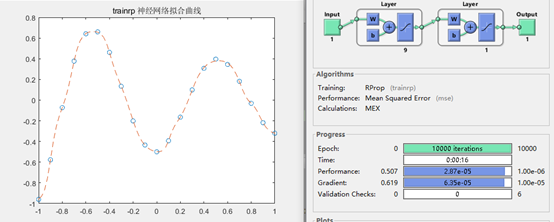
图6 训练函数为trainrp 拟合结果

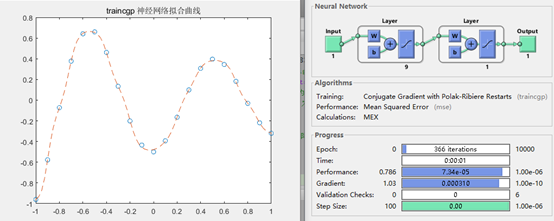
图7 训练函数为traincgp 拟合结果

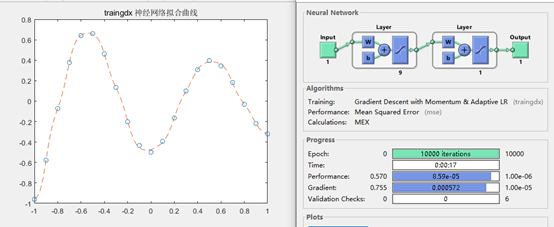
图8 训练函数为traingdx 拟合结果

　　可见，traingd、traingdm是较差的训练函数，收敛时间长；而训练函数trainrp/traincgp等性能一般，trainlm是较佳的训练函数，训练时间短，拟合效果佳。

3.4 函数关系式

　　MATLAB代码输入

　　得结果为：simy =

2/(exp(2534319068038565/(562949953421312*(exp((3631672591091961*x)

/140737488355328+6863392162896721/281474976710656)+1)) + 5718237858863659/(18014398509481984*(exp((7444114435060467*x)/281474976710656-2920590510334957/281474976710656)+1)) -4407302316599713/(2251799813685248*(exp(-(3121532728107483*x)/140737488355328 - 4422873762208683/281474976710656) +1))  +

6681843142583089/(18014398509481984*(exp(1623302466041475/70368744177664-(7266061041617473*x)/281474976710656)+1)) - 1132865518096015/(562949953421312*(exp(2512097340583147/1125899906842624-(1559249268373737*x)/140737488355328)+1)) + 6045060497805921/(4503599627370496*(exp(5296108181129999/562949953421312-(1862916351889959*x)/140737488355328)+1)) - 4804294000663935/(4503599627370496*(exp((847671511961421*x)/35184372088832+3450827515650845/562949953421312)+1)) + 6639507791072923/(9007199254740992*(exp(- (7400247294894263*x)/281474976710656 - 3347678857733481/1125899906842624) +1))   +

5470015743536569/(4503599627370496*(exp(- (1964472234771961*x)/70368744177664 - 3192411785409777/281474976710656) + 1)) + 18338633840740381/18014398509481984) + 1) - 1

参考文献

　　[1] 郝丽娜.计算机仿真技术及CAD.[M].北京.高等教育出版社.2014

　　[2] 孙帆，施学勤.基于MATLAB的BP神经网络设计[J].计算机与数字工程,2007,35(8)

　　[3]郑阿奇，曹戈.MATLAB实用教程[M].北京：电子工业出版社,2004，1-3