单片机复位电路仿真分析

I 单片机复位概述

1.1 复位机理

　　引脚RST保持2个机器周期以上的高电平

1.2 电路原理

　　电容刚接入电路时相当于短路，电容处于充电状态；当电容两极板充满电量后，电容相当于断路状态。根据电容充电时间效应，通过改变电容值及接入电阻值的大小，从而满足一定时长的高电平输出。

1.3 复位方式

图1复位电路图

1.3.1 上电复位

　　上电瞬间，电容充电电流最大，电容相当于短路，RST端为高电平，自动复位；电容两端的电压达到电源电压时，电容充电电流为零，电容相当于开路，RST端为低电平，程序正常运行。

1.3.2 手动复位

　　首先经过上电复位，当按下按键时，RST直接与VCC相连，为高电平形成复位，同时电解电容被短路放电；按键松开时，VCC对电容充电，充电电流在电阻上，RST依然为高电平，仍然是复位，充电完成后，电容相当于开路，RST为低电平，正常工作。

II 系统分析

2.1 模型简化

　　如图2，模型可简化为图示电路，其中，系统参数为C1和R2，系统控制输出量为，以电源接入为初始状态，即，对模型进行建模分析。

设定单片机的晶振为12MHZ，则两个机器周期为2ms。

 

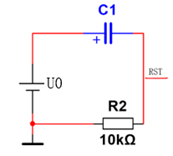
图2简化系统模型

2.2 模型假设

　　假设电路中的电阻阻值忽略不计；

　　假设电平变化为理想电平模式，即>1.5V为高电平，输出为1；<1.5V为低电平，输出为0。

2.3 微分方程

III 系统求解

3.1 微分方程求解

3.1.1 近似解

clear,clc
t0=0;
tN=0.5;%单位为s
h=0.001;
t=t0:h:tN;
N=length(t);
j=1;
y0=5;
for j=1:N
    tn=t0+h;
    k1=rk4(t0,y0);
    k2=rk4(t0+h/2,y0+h*k1/2);
    k3=rk4(t0+h/2,y0+h*k2/2);
    k4=rk4(t0+h,y0+h*k3);
    yn=y0+(h/6)*(k1+2*k2+2*k3+k4);
    yy(j)=yn;
    if yy(j)>=1.5
        y(j)=1;
    else
        y(j)=0;
    end
    t0=tn;
    y0=yn;
    j=j+1;
end
t=0:h:tN;
figure(1)
plot(t,yy,'r')
title('figure of RK_4 method')
xlabel('Time (s)')
ylabel('Value (y)')

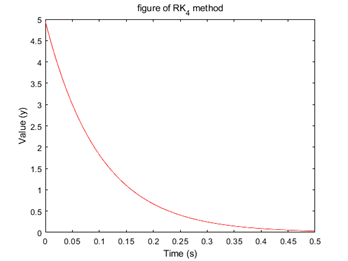
图3 近似解曲线图

figure(2)
plot(t,y,'b')
title('figure of Urst')
xlabel('Time (t)')
ylabel('Value (U)')
axis([0 0.5 -0.1 1.1])

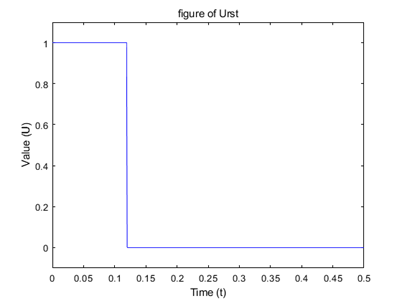
图4 电平模拟图

 

 

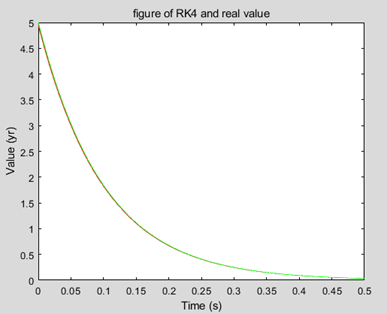
3.1.2 解析解

　　由方程

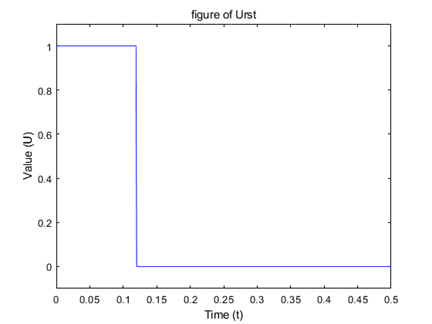
图6 电平与时间关系图

　　由图6可知，当t<0.12s时，输出为电平1，当t<0.12s时，输出为电平0.高电平持续时长大于2个机器周期。

（2）关于CR参数选取：

　　CR的取值与时长有直接关系，CR的取值有两种方式，其一，采用经验法，即模仿已有电路取相近值，再通过取增量进行仿真微调；其二，采用函数法，即根据上述方程，计算CR与时长的关系，从而根据t精准调节CR乘积值。

 

 

3.2.2 软件仿真

　　利用Multisim对该电路进行仿真，如下图：

图7 电路仿真原理图

　　设定相应的值，可以通过观察示波器显示电平的变化。由图8可知，当电平从5V下降到1.5V时，用时0.12s。

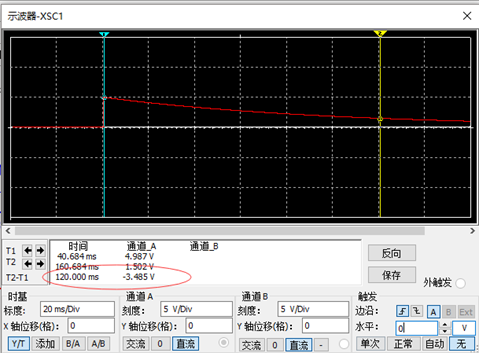
图8 示波器仿真图象

 

四、结论

　　由上述分析可知，当采用RC电路复位时，复位引脚电平与时间的关系式为：，经过仿真，可以发现，调整不同的CR值，可以得到不同的高电平持续时间。如果单片机晶振为12MHZ，那么复位电路的CR值可根据关系式进行调节。