四元数

四元数是一种在游戏引擎中比矩阵更适合表示旋转的表达形式：

1.之前的文章已经说过了矩阵旋转矩阵的推导，一个旋转至少要用3X3的矩阵表示，9个浮点数表示旋转显然是有冗余的，因为旋转只有3个自由度。

2.用矢量矩阵乘法来旋转矩阵，需要3个点积，即9个乘数和6个加数。若有可能，我们希望找到一种旋转表示方式，能加快旋转运算。

3.假设知道旋转A和旋转B，我们想要计算A和B之间的插值。矩阵的实现要比四元数复杂很多。

 

1.四元数的表示：

假设旋转的单位轴为qx，qy，qz，qw，旋转的角度为θ，旋转方向遵循右手法则，那么这个旋转可以表示为

x，y，z为矢量部分，w为标量部分，所以也可以简化表示为：

 

其中a为旋转轴方向的单位矢量

 

2.四元数的乘法：

用于四元数上的最重要运算之一就是乘法。给定两个四元数p和q，分别代表旋转P和Q，则pq代表两旋转的合成旋转（即旋转Q之后再旋转P）。其实四元数乘法有几种，这里只讨论1和三维旋转应用相关的乘法，此乘法称为格拉斯曼积：

     

其中V代表矢量部分，s表示标量部分

 

3.共轭及逆四元数：

要计算逆四元数，先要定义一个称为共轭的量，共轭通常写为q*：

 

换句话说，共轭是矢量部分求反，但标量部分保持不变。

 

逆四元数q^-1可以表示为：

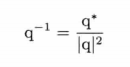
 由于我们使用的四元数都是用于代表三维旋转的，这些四元数都是单位长度的。因此，这种情况下，共轭和逆四元数是相等的

我们可以利用这一点优化引擎

 

4.积的共轭及逆四元数

 

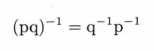
5.以四元数旋转矢量

1.首先要把矢量重写为四元数形式，对于一个矢量v，他的四元数矢量部分就是他自己本身，标量部分为0，即[v_x, v_y, v_z, 0]

2.要以四元数q旋转矢量v，须用q前乘以矢量v，然后再乘以逆四元数q^-1旋转后的矢量v’可如下得出：

因为旋转用的四元数都是单位长度的，所以使用共轭也是等同的：

只要从v’中提取矢量部分，就能得到我们旋转后的矢量v’

 

6.旋转性的线性插值

最简单快速的旋转插值方法，就是套用四维矢量的线性插值（LERP）至四元数。给定两个分别代表旋转A和旋转B的四元数q_a和q_b，可以找出旋转A至旋转B之间β百分点的中间旋转q_LERP：

注意插值后的四元数需要再归一。这是因为LERP运算一般来说并不保持矢量长度。

 

7.球面线性插值SLERP

不做详述

 

 以上内容摘自《游戏引擎架构》