Day 8 - 并查集、堆、set 与 map

合集 - 2024 暑假(51)

1.2024 暑假记2024-08-162.Day 1 - 二分2024-07-083.Day 1 - 题目集2024-07-084.Day 2 - 分治、倍增、LCA 与树链剖分2024-07-095.Day 2 - 题目集2024-07-096.Day 3 - 单调栈、单调队列、凸包与斜率优化2024-07-107.Day 3 - 题目集2024-07-108.Day 4 - 搜索进阶与模拟2024-07-119.Day 4 - 题目集2024-07-1110.Day 5 - 双指针与折半搜索2024-07-1211.Day 5 - 题目集2024-07-1212.Day 7 - 哈希与 KMP2024-07-1413.Day 7 - 题目集2024-07-14

14.Day 8 - 并查集、堆、set 与 map2024-07-15

15.Day 8 - 题目集2024-07-1516.Day 9 - 线段树2024-07-1617.Day 9 - 题目集2024-07-1718.Day 10 - 动态规划与树状数组2024-07-1719.Day 10 - 题目集2024-07-1720.Day 11 - 模拟赛2024-07-1821.Day 11 - 题目集2024-07-1822.Day 13 - 树形 DP 与换根 DP2024-07-2023.Day 13 - 题目集2024-07-2024.Day 14 - 模拟赛2024-07-2125.Day 14 - 题目集2024-07-2126.Day 15 - 数位 DP 与状压 DP2024-07-2227.Day 15 - 题目集2024-07-2228.Day 16 - 模拟赛2024-07-2329.Day 16 - 题目集2024-07-2330.Day 17 - 贪心2024-07-2431.Day 17 - 题目集2024-07-2432.Day 19 - 构造、转换与模拟2024-07-2633.Day 19 - 题目集2024-07-2634.Day 20 - 最短路与差分约束2024-07-2735.Day 20 - 题目集2024-07-2736.Day 21 - 最小生成树2024-07-2837.Day 21 - 题目集2024-07-2838.Day 22 - 图论联通性2024-07-2939.Day 22 - 题目集2024-07-2940.Day 23 - 模拟赛2024-07-3041.Day 23 - 题目集2024-07-3042.Day 25 - 同余与乘法逆元2024-08-0143.Day 25 - 题目集2024-08-0144.Day 26 - 模拟赛2024-08-0245.Day 26 - 题目集2024-08-0346.Day 27 - 欧几里得算法与中国剩余定理2024-08-0347.Day 27 - 题目集2024-08-0348.Day 28 - 组合数学与矩阵初步2024-08-0449.Day 28 - 题目集2024-08-0450.Day 29 - 结营测试2024-08-0551.Day 29 - 题目集2024-08-05

收起

1|0并查集

1|1引入

并查集是一种用于管理元素所属集合的数据结构，实现为一个森林，其中每棵树表示一个集合，树中的节点表示对应集合中的元素。

顾名思义，并查集支持两种操作：

• 合并（$\text{Union}$）：合并两个元素所属集合（合并对应的树）
• 查询（$\text{Find}$）：查询某个元素所属集合（查询对应的树的根节点），这可以用于判断两个元素是否属于同一集合

并查集在经过修改后可以支持单个元素的删除、移动；使用动态开点线段树还可以实现可持久化并查集。

并查集无法以较低复杂度实现集合的分离。

1|2初始化

初始时，每个元素都位于一个单独的集合，表示为一棵只有根节点的树。方便起见，我们将根节点的父亲设为自己。

实现：

struct dsu {
    vector<size_t> pa;

    explicit dsu(size_t size) : pa(size) { iota(pa.begin(), pa.end(), 0); }
};

1|3查询

我们需要沿着树向上移动，直至找到根节点。

实现：

size_t dsu::find(size_t x) { return pa[x] == x ? x : find(pa[x]); }

1|0路径压缩

查询过程中经过的每个元素都属于该集合，我们可以将其直接连到根节点以加快后续查询。

实现：

size_t dsu::find(size_t x) { return pa[x] == x ? x : pa[x] = find(pa[x]); }

1|4合并

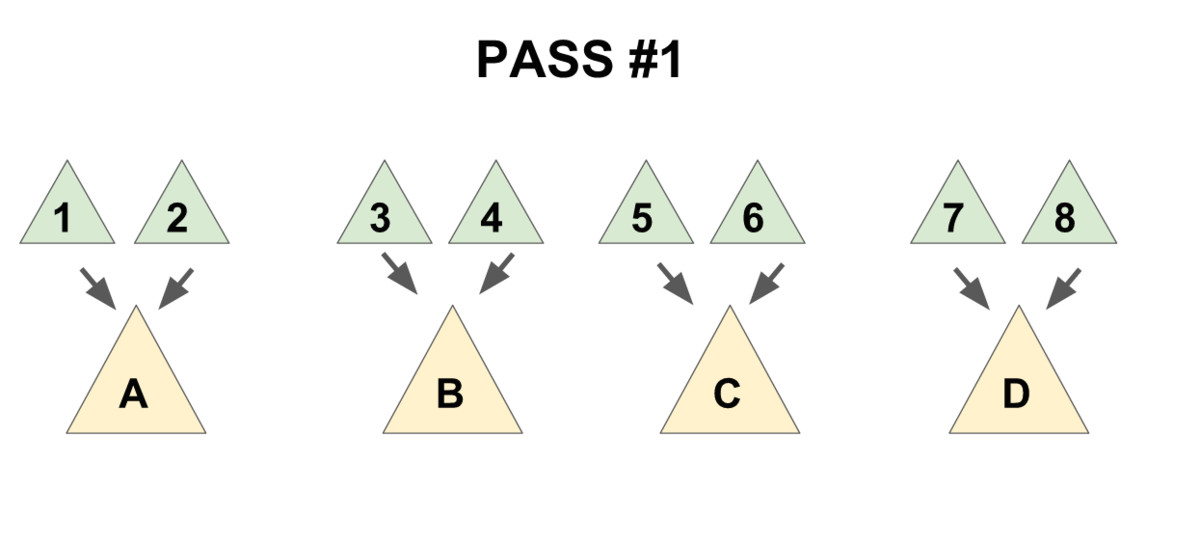
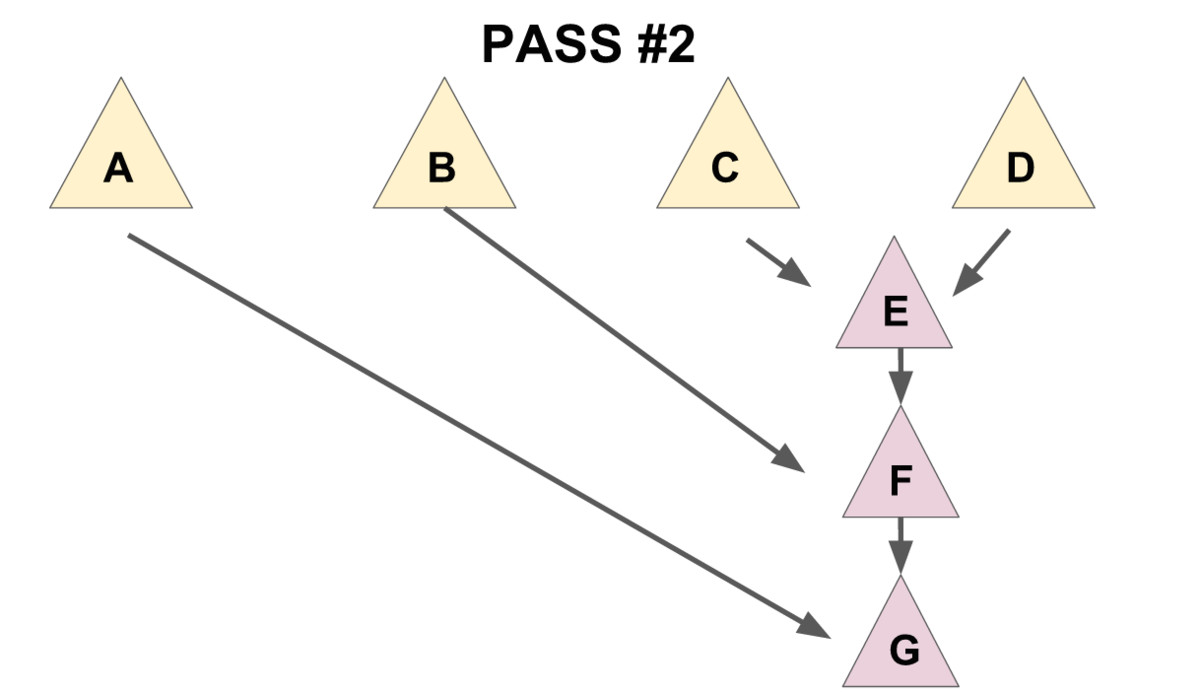
要合并两棵树，我们只需要将一棵树的根节点连到另一棵树的根节点。

实现：

void dsu::unite(size_t x, size_t y) { pa[find(x)] = find(y); }

1|0启发式合并

合并时，选择哪棵树的根节点作为新树的根节点会影响未来操作的复杂度。我们可以将节点较少或深度较小的树连到另一棵，以免发生退化。

具体复杂度讨论：

由于需要我们支持的只有集合的合并、查询操作，当我们需要将两个集合合二为一时，无论将哪一个集合连接到另一个集合的下面，都能得到正确的结果。但不同的连接方法存在时间复杂度的差异。具体来说，如果我们将一棵点数与深度都较小的集合树连接到一棵更大的集合树下，显然相比于另一种连接方案，接下来执行查找操作的用时更小（也会带来更优的最坏时间复杂度）。

当然，我们不总能遇到恰好如上所述的集合——点数与深度都更小。鉴于点数与深度这两个特征都很容易维护，我们常常从中择一，作为估价函数。而无论选择哪一个，时间复杂度都为 $O(m\alpha (m,n))$，具体的证明可参见 $\text{References}$ 中引用的论文。

在算法竞赛的实际代码中，即便不使用启发式合并，代码也往往能够在规定时间内完成任务。在 Tarjan 的论文${}^{\text{tarjan1984worst}}$中，证明了不使用启发式合并、只使用路径压缩的最坏时间复杂度是 $O(m\log n)$。在姚期智的论文${}^{\text{yao1985expected}}$中，证明了不使用启发式合并、只使用路径压缩，在平均情况下，时间复杂度依然是 $O(m\alpha (m,n))$。

如果只使用启发式合并，而不使用路径压缩，时间复杂度为 $O(m\log n)$。由于路径压缩单次合并可能造成大量修改，有时路径压缩并不适合使用。例如，在可持久化并查集、线段树分治 + 并查集中，一般使用只启发式合并的并查集。

按节点数合并的参考实现：

实现：

struct dsu {
    vector<size_t> pa, size;

    explicit dsu(size_t size_) : pa(size_), size(size_, 1) {
    iota(pa.begin(), pa.end(), 0);
    }

    void unite(size_t x, size_t y) {
    x = find(x), y = find(y);
    if (x == y) return;
    if (size[x] < size[y]) swap(x, y);
    pa[y] = x;
    size[x] += size[y];
    }
};

1|5删除

要删除一个叶子节点，我们可以将其父亲设为自己。为了保证要删除的元素都是叶子，我们可以预先为每个节点制作副本，并将其副本作为父亲。

实现：

struct dsu {
    vector<size_t> pa, size;

    explicit dsu(size_t size_) : pa(size_ * 2), size(size_ * 2, 1) {
    iota(pa.begin(), pa.begin() + size_, size_);
    iota(pa.begin() + size_, pa.end(), size_);
    }

    void erase(size_t x) {
    --size[find(x)];
    pa[x] = x;
    }
};

1|6移动

与删除类似，通过以副本作为父亲，保证要移动的元素都是叶子。

实现：

void dsu::move(size_t x, size_t y) {
    auto fx = find(x), fy = find(y);
    if (fx == fy) return;
    pa[x] = fy;
    --size[fx], ++size[fy];
}

1|7复杂度

1|0时间复杂度

同时使用路径压缩和启发式合并之后，并查集的每个操作平均时间仅为 $O(\alpha (n))$，其中 $\alpha$ 为阿克曼函数的反函数，其增长极其缓慢，也就是说其单次操作的平均运行时间可以认为是一个很小的常数。

$\text{Ackermann}$ 函数 $A(m,n)$ 的定义是这样的：

$A(m,n)=\{\begin{array}{ll}n+1& \text{if }m=0\\ A(m-1,1)& \text{if }m>0\text{ and }n=0\\ A(m-1,A(m,n-1))& \text{otherwise}\end{array}$

而反 $\text{Ackermann}$ 函数 $\alpha (n)$ 的定义是阿克曼函数的反函数，即为最大的整数 $m$ 使得 $A(m,m)⩽n$。

1|0空间复杂度

显然为 $O(n)$。

1|8带权并查集

我们还可以在并查集的边上定义某种权值、以及这种权值在路径压缩时产生的运算，从而解决更多的问题。比如对于经典的「$\text{NOI2001}$」食物链，我们可以在边权上维护模 $3$ 意义下的加法群。

1|9例题

UVa11987 Almost Union-Find。

实现类似并查集的数据结构，支持以下操作：

1. 合并两个元素所属集合
2. 移动单个元素
3. 查询某个元素所属集合的大小及元素和

#include <bits/stdc++.h>

using namespace std;

struct dsu {
  vector<size_t> pa, size, sum;

  explicit dsu(size_t size_)
      : pa(size_ * 2), size(size_ * 2, 1), sum(size_ * 2) {
    // size 与 sum 的前半段其实没有使用，只是为了让下标计算更简单
    iota(pa.begin(), pa.begin() + size_, size_);
    iota(pa.begin() + size_, pa.end(), size_);
    iota(sum.begin() + size_, sum.end(), 0);
  }

  void unite(size_t x, size_t y) {
    x = find(x), y = find(y);
    if (x == y) return;
    if (size[x] < size[y]) swap(x, y);
    pa[y] = x;
    size[x] += size[y];
    sum[x] += sum[y];
  }

  void move(size_t x, size_t y) {
    auto fx = find(x), fy = find(y);
    if (fx == fy) return;
    pa[x] = fy;
    --size[fx], ++size[fy];
    sum[fx] -= x, sum[fy] += x;
  }

  size_t find(size_t x) { return pa[x] == x ? x : pa[x] = find(pa[x]); }
};

int main() {
  size_t n, m, op, x, y;
  while (cin >> n >> m) {
    dsu dsu(n + 1);  // 元素范围是 1..n
    while (m--) {
      cin >> op;
      switch (op) {
        case 1:
          cin >> x >> y;
          dsu.unite(x, y);
          break;
        case 2:
          cin >> x >> y;
          dsu.move(x, y);
          break;
        case 3:
          cin >> x;
          x = dsu.find(x);
          cout << dsu.size[x] << ' ' << dsu.sum[x] << '\n';
          break;
        default:
          assert(false);  // not reachable
      }
    }
  }
}

1|10习题

「NOI2015」程序自动分析

「JSOI2008」星球大战

「NOI2001」食物链

「NOI2002」银河英雄传说

1|11其他应用

最小生成树算法中的 $\text{Kruskal}$ 和最近公共祖先中的 $\text{Tarjan}$ 算法是基于并查集的算法。

1|12参考资料与拓展阅读

1. 知乎回答：是否在并查集中真的有二分路径压缩优化？
2. Gabow, H. N., & Tarjan, R. E. (1985). A Linear-Time Algorithm for a Special Case of Disjoint Set Union. JOURNAL OF COMPUTER AND SYSTEM SCIENCES, 30, 209-221.PDF

${}^{\text{tarjan1984worst}}$: Tarjan, R. E., & Van Leeuwen, J. (1984). Worst-case analysis of set union algorithms. Journal of the ACM (JACM), 31(2), 245-281.ResearchGate PDF

${}^{\text{yao1985expected}}$: Yao, A. C. (1985). On the expected performance of path compression algorithms.SIAM Journal on Computing, 14(1), 129-133.

2|0并查集时间复杂度

本部分内容转载并修改自 时间复杂度 - 势能分析浅谈，已取得原作者授权同意。

2|1定义

1|0阿克曼函数

这里，先给出 $\alpha (n)$ 的定义。为了给出这个定义，先给出 $A_k(j)$ 的定义。

定义 $A_k(j)$ 为：

$$A_k(j)=\{\begin{array}{rlrlr}& j+1& & k=0& \\ & A_{k-1}^{(j+1)}(j)& & k\ge 1& \end{array}$$

即阿克曼函数。

这里，$f^i(x)$ 表示将 $f$ 连续应用在 $x$ 上 $i$ 次，即 $f^0(x)=x$，$f^i(x)=f(f^{i-1}(x))$。

再定义 $\alpha (n)$ 为使得 $A_{\alpha (n)}(1)\ge n$ 的最小整数值。注意，我们之前将它描述为 $A_{\alpha (n)}(\alpha (n))\ge n$，反正他们的增长速度都很慢，值都不超过 4。

1|0基础定义

每个节点都有一个 rank。这里的 rank 不是节点个数，而是深度。节点的初始 rank 为 0，在合并的时候，如果两个节点的 rank 不同，则将 rank 小的节点合并到 rank 大的节点上，并且不更新大节点的 rank 值。否则，随机将某个节点合并到另外一个节点上，将根节点的 rank 值 +1。这里根节点的 rank 给出了该树的高度。记 x 的 rank 为 $rnk(x)$，类似的，记 x 的父节点为 $fa(x)$。我们总有 $rnk(x)+1\le rnk(fa(x))$。

为了定义势函数，需要预先定义一个辅助函数 $level(x)$。其中，$level(x)=max(k:rnk(fa(x))\ge A_k(rnk(x)))$。当 $rnk(x)\ge 1$ 的时候，再定义一个辅助函数 $iter(x)=max(i:rnk(fa(x))\ge A_{level(x)}^i(rnk(x))$。这些函数定义的 $x$ 都满足 $rnk(x)>0$ 且 $x$ 不是某个树的根。

上面那些定义可能让你有点头晕。再理一下，对于一个 $x$ 和 $fa(x)$，如果 $rnk(x)>0$，总是可以找到一对 $i,k$ 令 $rnk(fa(x))\ge A_k^i(rnk(x))$，而 $level(x)=max(k)$，在这个前提下，$iter(x)=max(i)$。$level$ 描述了 $A$ 的最大迭代级数，而 $iter$ 描述了在最大迭代级数时的最大迭代次数。

对于这两个函数，$level(x)$ 总是随着操作的进行而增加或不变，如果 $level(x)$ 不增加，$iter(x)$ 也只会增加或不变。并且，它们总是满足以下两个不等式：

$$0\le level(x)<\alpha (n)$$

$$1\le iter(x)\le rnk(x)$$

考虑 $level(x)$、$iter(x)$ 和 $A_k^j$ 的定义，这些很容易被证明出来，就留给读者用于熟悉定义了。

定义势能函数 $\mathrm{\Phi }(S)=\sum _{x\in S}\mathrm{\Phi }(x)$，其中 $S$ 表示一整个并查集，而 $x$ 为并查集中的一个节点。定义 $\mathrm{\Phi }(x)$ 为：

$$\mathrm{\Phi }(x)=\{\begin{array}{ll}\alpha (n)\times \mathit{rnk}(x)& \mathit{rnk}(x)=0\text{或}x\text{为某棵树的根节点}\\ (\alpha (n)-\mathit{level}(x))\times \mathit{rnk}(x)-iter(x)& \text{otherwise}\end{array}$$

然后就是通过操作引起的势能变化来证明摊还时间复杂度为 $\mathrm{\Theta }(\alpha (n))$ 啦。注意，这里我们讨论的 $union(x,y)$ 操作保证了 $x$ 和 $y$ 都是某个树的根，因此不需要额外执行 $find(x)$ 和 $find(y)$。

可以发现，势能总是个非负数。另，在开始的时候，并查集的势能为 $0$。

2|2证明

1|0union(x,y) 操作

其花费的时间为 $\mathrm{\Theta }(1)$，因此我们考虑其引起的势能的变化。

这里，我们假设 $rnk(x)\le rnk(y)$，即 $x$ 被接到 $y$ 上。这样，势能增加的节点仅有 $x$（从树根变成非树根），$y$（秩可能增加）和操作前 $y$ 的子节点（父节点的秩可能增加）。我们先证明操作前 $y$ 的子节点 $c$ 的势能不可能增加，并且如果减少了，至少减少 $1$。

设操作前 $c$ 的势能为 $\mathrm{\Phi }(c)$，操作后为 $\mathrm{\Phi }(c^{\prime })$，这里 $c$ 可以是任意一个 $rnk(c)>0$ 的非根节点，操作可以是任意操作，包括下面的 find 操作。我们分三种情况讨论。

1. $iter(c)$ 和 $level(c)$ 并未增加。显然有 $\mathrm{\Phi }(c)=\mathrm{\Phi }(c^{\prime })$。
2. $iter(c)$ 增加了，$level(c)$ 并未增加。这里 $iter(c)$ 至少增加一，即 $\mathrm{\Phi }(c^{\prime })\le \mathrm{\Phi }(c)-1$，势能函数减少了，并且至少减少 1。
3. $level(c)$ 增加了，$iter(c)$ 可能减少。但是由于 $0<iter(c)\le rnk(c)$，$iter(c)$ 最多减少 $rnk(c)-1$，而 $level(c)$ 至少增加 $1$。由定义 $\mathrm{\Phi }(c)=(\alpha (n)-level(c))\times rnk(c)-iter(c)$，可得 $\mathrm{\Phi }(c^{\prime })\le \mathrm{\Phi }(c)-1$。
4. 其他情况。由于 $rnk(c)$ 不变，$rnk(fa(c))$ 不减，所以不存在。

所以，势能增加的节点仅可能是 $x$ 或 $y$。而 $x$ 从树根变成了非树根，如果 $rnk(x)=0$，则一直有 $\mathrm{\Phi }(x)=\mathrm{\Phi }(x^{\prime })=0$。否则，一定有 $\alpha (x)\times rnk(x)\ge (\alpha (n)-level(x))\times rnk(x)-iter(x)$。即，$\mathrm{\Phi }(x^{\prime })\le \mathrm{\Phi }(x)$。

因此，唯一势能可能增加的点就是 $y$。而 $y$ 的势能最多增加 $\alpha (n)$。因此，可得 $union$ 操作均摊后的时间复杂度为 $\mathrm{\Theta }(\alpha (n))$。

1|0find(a) 操作

如果查找路径包含 $\mathrm{\Theta }(s)$ 个节点，显然其查找的时间复杂度是 $\mathrm{\Theta }(s)$。如果由于查找操作，没有节点的势能增加，且至少有 $s-\alpha (n)$ 个节点的势能至少减少 $1$，就可以证明 $find(a)$ 操作的时间复杂度为 $\mathrm{\Theta }(\alpha (n))$。为了避免混淆，这里用 $a$ 作为参数，而出现的 $x$ 都是泛指某一个并查集内的结点。

首先证明没有节点的势能增加。很显然，我们在上面证明过所有非根节点的势能不增，而根节点的 $rnk$ 没有改变，所以没有节点的势能增加。

接下来证明至少有 $s-\alpha (n)$ 个节点的势能至少减少 $1$。我们上面证明过了，如果 $level(x)$ 或者 $iter(x)$ 有改变的话，它们的势能至少减少 $1$。所以，只需要证明至少有 $s-\alpha (n)$ 个节点的 $level(x)$ 或者 $iter(x)$ 有改变即可。

回忆一下非根节点势能的定义，$\mathrm{\Phi }(x)=(\alpha (n)-level(x))\times rnk(x)-iter(x)$，而 $level(x)$ 和 $iter(x)$ 是使 $rnk(fa(x))\ge A_{level(x)}^{iter(x)}(rnk(x))$ 的最大数。

所以，如果 $roo{t}_x$ 代表 $x$ 所处的树的根节点，只需要证明 $rnk(roo{t}_x)\ge A_{level(x)}^{iter(x)+1}(rnk(x))$ 就好了。根据 $A_k^i$ 的定义，$A_{level(x)}^{iter(x)+1}(rnk(x))=A_{level(x)}(A_{level(x)}^{iter(x)}(rnk(x)))$。

注意，我们可能会用 $k(x)$ 代表 $level(x)$，$i(x)$ 代表 $iter(x)$ 以避免式子过于冗长。这里，就是 $rnk(roo{t}_x)\ge A_{k(x)}(A_{k(x)}^{i(x)}(x))$。

当你看到这的时候，可能会有一种「这啥玩意」的感觉。这意味着你可能需要多看几遍，或者跳过一些内容以后再看。

这里，我们需要一个外接的 $A_{k(x)}$，意味着我们可能需要再找一个点 $y$。令 $y$ 是搜索路径上在 $x$ 之后的满足 $k(y)=k(x)$ 的点，这里「搜索路径之后」相当于「是 $x$ 的祖先」。显然，不是每一个 $x$ 都有这样一个 $y$。很容易证明，没有这样的 $y$ 的 $x$ 不超过 $\alpha (n)-2$ 个。因为只有每个 $k$ 的最后一个 $x$ 和 $a$ 以及 $roo{t}_a$ 没有这样的 $y$。

我们再强调一遍 $fa(x)$ 指的是路径压缩 之前 $x$ 的父节点，路径压缩 之后 $x$ 的父节点一律用 $roo{t}_x$ 表示。对于每个存在 $y$ 的 $x$，总是有 $rnk(y)\ge rnk(fa(x))$。同时，我们有 $rnk(fa(x))\ge A_{k(x)}^{i(x)}(rnk(x))$。由于 $k(x)=k(y)$，我们用 $k$ 来统称，即，$rnk(fa(x))\ge A_k^{i(x)}(rnk(x))$。我们需要造一个 $A_k$ 出来，所以我们可以不关注 $iter(y)$ 的值，直接使用弱化版的 $rnk(fa(y))\ge A_k(rnk(y))$。

如果我们将不等式组合起来，神奇的事情就发生了。我们发现，$rnk(fa(y))\ge A_k^{i(x)+1}(rnk(x))$。也就是说，为了从 $rnk(x)$ 迭代到 $rnk(fa(y))$，至少可以迭代 $A_k$ 不少于 $i(x)+1$ 次而不超过 $rnk(fa(y))$。

显然，有 $rnk(roo{t}_y)\ge rnk(fa(y))$，且 $rnk(x)$ 在路径压缩时不变。因此，我们可以得到 $rnk(roo{t}_x)\ge A_k^{i(x)+1}(rnk(x))$，也就是说 $iter(x)$ 的值至少增加 1，如果 $rnk(x)$ 没有增加，一定是 $level(x)$ 增加了。

所以，$\mathrm{\Phi }(x)$ 至少减少了 1。由于这样的 $x$ 节点至少有 $s-\alpha (n)-2$ 个，所以最后 $\mathrm{\Phi }(S)$ 至少减少了 $s-\alpha (n)-2$，均摊后的时间复杂度即为 $\mathrm{\Theta }(\alpha (n)+2)=\mathrm{\Theta }(\alpha (n))$。

2|3为何并查集会被卡

这个问题也就是问，如果我们不按秩合并，会有哪些性质被破坏，导致并查集的时间复杂度不能保证为 $\mathrm{\Theta }(m\alpha (n))$。

如果我们在合并的时候，$rnk$ 较大的合并到了 $rnk$ 较小的节点上面，我们就将那个 $rnk$ 较小的节点的 $rnk$ 值设为另一个节点的 $rnk$ 值加一。这样，我们就能保证 $rnk(fa(x))\ge rnk(x)+1$，从而不会出现类似于满地 compile error 一样的性质不符合。

显然，如果这样子的话，我们破坏的就是 $union(x,y)$ 函数「y 的势能最多增加 $\alpha (n)$」这一句。

存在一个能使路径压缩并查集时间复杂度降至 $\mathrm{\Omega }(m{\log }_{1+\frac{m}{n}}n)$ 的结构，定义如下：

二项树（实际上和一般的二项树不太一样），其中 j 是常数，$T_k$ 为一个 $T_{k-1}$ 加上一个 $T_{k-j}$ 作为根节点的儿子。

边界条件，$T_1$ 到 $T_j$ 都是一个单独的点。

令 $rnk(T_k)=r_k$，这里我们有 $r_k=(k-1)/j$（证明略）。每轮操作，我们将它接到一个单节点上，然后查询底部的 $j$ 个节点。也就是说，我们接到单节点上的时候，单节点的势能提高了 $(k-1)/j+1$。在 $j=\lfloor \frac{m}{n}\rfloor$，$i=\lfloor {\log }_{j+1}\frac{n}{2}\rfloor$，$k=ij$ 的时候，势能增加量为：

$$\alpha (n)\times ((ij-1)/j+1)=\alpha (n)\times ((\lfloor {\log }_{\lfloor \frac{m}{n}\rfloor +1}\frac{n}{2}\rfloor \times \lfloor \frac{m}{n}\rfloor -1)/\lfloor \frac{m}{n}\rfloor +1)$$

变换一下，去掉所有的取整符号，就可以得出，势能增加量 $\ge \alpha (n)\times ({\log }_{1+\frac{m}{n}}n-\frac{n}{m})$，m 次操作就是 $\mathrm{\Omega }(m{\log }_{1+\frac{m}{n}}n-n)=\mathrm{\Omega }(m{\log }_{1+\frac{m}{n}}n)$。

2|4关于启发式合并

由于按秩合并比启发式合并难写，所以很多 dalao 会选择使用启发式合并来写并查集。具体来说，则是对每个根都维护一个 $size(x)$，每次将 $size$ 小的合并到大的上面。

所以，启发式合并会不会被卡？

首先，可以从秩参与证明的性质来说明。如果 $size$ 可以代替 $rnk$ 的地位，则可以使用启发式合并。快速总结一下，秩参与证明的性质有以下三条：

1. 每次合并，最多有一个节点的秩上升，而且最多上升 1。
2. 总有 $rnk(fa(x))\ge rnk(x)+1$。
3. 节点的秩不减。

关于第二条和第三条，$siz$ 显然满足，然而第一条不满足，如果将 $x$ 合并到 $y$ 上面，则 $siz(y)$ 会增大 $siz(x)$ 那么多。

所以，可以考虑使用 ${\log }_{2}siz(x)$ 代替 $rnk(x)$。

关于第一条性质，由于节点的 $siz$ 最多翻倍，所以 ${\log }_{2}siz(x)$ 最多上升 1。关于第二三条性质，结论较为显然，这里略去证明。

所以说，如果不想写按秩合并，就写启发式合并好了，时间复杂度仍旧是 $\mathrm{\Theta }(m\alpha (n))$。

3|0堆

堆是一棵树，其每个节点都有一个键值，且每个节点的键值都大于等于/小于等于其父亲的键值。

每个节点的键值都大于等于其父亲键值的堆叫做小根堆，否则叫做大根堆。STL 中的 priority_queue 其实就是一个大根堆。

（小根）堆主要支持的操作有：插入一个数、查询最小值、删除最小值、合并两个堆、减小一个元素的值。

一些功能强大的堆（可并堆）还能（高效地）支持 $\text{merge}$ 等操作。

一些功能更强大的堆还支持可持久化，也就是对任意历史版本进行查询或者操作，产生新的版本。

3|1堆的分类

操作 \ 数据结构${}^4$	配对堆	二叉堆	左偏树	二项堆	斐波那契堆
插入（insert）	$O(1)$	$O(\log n)$	$O(\log n)$	$O(\log n{)}^1$	$O(1)$
查询最小值（find-min）	$O(1)$	$O(1)$	$O(1)$	$O(1{)}^{23}$	$O(1)$
删除最小值（delete-min）	$O(\log n{)}^3$	$O(\log n)$	$O(\log n)$	$O(\log n)$	$O(\log n{)}^3$
合并 (merge)	$O(1)$	$O(n)$	$O(\log n)$	$O(\log n)$	$O(1)$
减小一个元素的值 (decrease-key)	$o(\log n)$（下界 $\mathrm{\Omega }(\log \log n)$，上界 $O(2^{2\sqrt{\log \log n}})$）${}^3$	$O(\log n)$	$O(\log n)$	$O(\log n)$	$O(1{)}^3$
是否支持可持久化	$\times$	$✓$	$✓$	$✓$	$\times$

${}^1$: 单次插入的复杂度为 $O(\log n)$，但有 $k$ 次连续插入时，可创建一个只包含要插入元素的二项堆，再将此堆与原先的二项堆进行合并，均摊复杂度为 $O(1)$

${}^2$: 可以保存一个指向最小元素的指针，在执行其他操作时修改该指针，即可在 $O(1)$ 的复杂度下进行查询了

${}^3$: 复杂度为均摊复杂度

${}^4$: 表格来自于 Wikipedia

习惯上，不加限定提到「堆」时往往都指二叉堆。

4|0二叉堆

4|1结构

从二叉堆的结构说起，它是一棵二叉树，并且是完全二叉树，每个结点中存有一个元素（或者说，有个权值）。

堆性质：父亲的权值不小于儿子的权值（大根堆）。同样的，我们可以定义小根堆。本文以大根堆为例。

由堆性质，树根存的是最大值（$\text{getmax}$ 操作就解决了）。

4|2过程

1|0插入操作

插入操作是指向二叉堆中插入一个元素，要保证插入后也是一棵完全二叉树。

最简单的方法就是，最下一层最右边的叶子之后插入。

如果最下一层已满，就新增一层。

插入之后可能会不满足堆性质？

向上调整：如果这个结点的权值大于它父亲的权值，就交换，重复此过程直到不满足或者到根。

可以证明，插入之后向上调整后，没有其他结点会不满足堆性质。

向上调整的时间复杂度是 $O(\log n)$ 的。

1|0删除操作

删除操作指删除堆中最大的元素，即删除根结点。

但是如果直接删除，则变成了两个堆，难以处理。

所以不妨考虑插入操作的逆过程，设法将根结点移到最后一个结点，然后直接删掉。

然而实际上不好做，我们通常采用的方法是，把根结点和最后一个结点直接交换。

于是直接删掉（在最后一个结点处的）根结点，但是新的根结点可能不满足堆性质……

向下调整：在该结点的儿子中，找一个最大的，与该结点交换，重复此过程直到底层。

可以证明，删除并向下调整后，没有其他结点不满足堆性质。

时间复杂度 $O(\log n)$。

1|0增加某个点的权值

很显然，直接修改后，向上调整一次即可，时间复杂度为 $O(\log n)$。

4|3实现

我们发现，上面介绍的几种操作主要依赖于两个核心：向上调整和向下调整。

考虑使用一个序列 $h$ 来表示堆。$h_i$ 的两个儿子分别是 $h_{2i}$ 和 $h_{2i+1}$，$1$ 是根结点：

参考代码：

void up(int x) {
  while (x > 1 && h[x] > h[x / 2]) {
    swap(h[x], h[x / 2]);
    x /= 2;
  }
}

void down(int x) {
  while (x * 2 <= n) {
    t = x * 2;
    if (t + 1 <= n && h[t + 1] > h[t]) t++;
    if (h[t] <= h[x]) break;
    std::swap(h[x], h[t]);
    x = t;
  }
}

1|0建堆

考虑这么一个问题，从一个空的堆开始，插入 $n$ 个元素，不在乎顺序。

直接一个一个插入需要 $O(n\log n)$ 的时间，有没有更好的方法？

1|0方法一：使用 decreasekey（即，向上调整）

从根开始，按 $\text{BFS}$ 序进行。

void build_heap_1() {
  for (i = 1; i <= n; i++) up(i);
}

为啥这么做：对于第 $k$ 层的结点，向上调整的复杂度为 $O(k)$ 而不是 $O(\log n)$。

总复杂度：$\log 1+\log 2+\cdots +\log n=\mathrm{\Theta }(n\log n)$。

（在「基于比较的排序」中证明过）

1|0方法二：使用向下调整

这时换一种思路，从叶子开始，逐个向下调整

void build_heap_2() {
  for (i = n; i >= 1; i--) down(i);
}

换一种理解方法，每次「合并」两个已经调整好的堆，这说明了正确性。

注意到向下调整的复杂度，为 $O(\log n-k)$，另外注意到叶节点无需调整，因此可从序列约 $n/2$ 的位置开始调整，可减少部分常数但不影响复杂度。

证明：

$$\begin{array}{rl}\text{总复杂度}& =n\log n-\log 1-\log 2-\cdots -\log n\\ & \le n\log n-0\times 2^0-1\times 2^1-\cdots -(\log n-1)\times \frac{n}{2}\\ & =n\log n-(n-1)-(n-2)-(n-4)-\cdots -(n-\frac{n}{2})\\ & =n\log n-n\log n+1+2+4+\cdots +\frac{n}{2}\\ & =n-1\\ & =O(n)\end{array}$$

之所以能 $O(n)$ 建堆，是因为堆性质很弱，二叉堆并不是唯一的。

要是像排序那样的强条件就难说了。

4|4应用

1|0对顶堆

SPOJ RMID2 - Running Median Again。

维护一个序列，支持两种操作：

1. 向序列中插入一个元素
2. 输出并删除当前序列的中位数（若序列长度为偶数，则输出较小的中位数）

这个问题可以被进一步抽象成：动态维护一个序列上第 $k$ 大的数，$k$ 值可能会发生变化。

对于此类问题，我们可以使用 对顶堆 这一技巧予以解决（可以避免写权值线段树或 BST 带来的繁琐）。

对顶堆由一个大根堆与一个小根堆组成，小根堆维护大值即前 $k$ 大的值（包含第 k 个），大根堆维护小值即比第 $k$ 大数小的其他数。

这两个堆构成的数据结构支持以下操作：

• 维护：当小根堆的大小小于 $k$ 时，不断将大根堆堆顶元素取出并插入小根堆，直到小根堆的大小等于 $k$；当小根堆的大小大于 $k$ 时，不断将小根堆堆顶元素取出并插入大根堆，直到小根堆的大小等于 $k$；
• 插入元素：若插入的元素大于等于小根堆堆顶元素，则将其插入小根堆，否则将其插入大根堆，然后维护对顶堆；
• 查询第 $k$ 大元素：小根堆堆顶元素即为所求；
• 删除第 $k$ 大元素：删除小根堆堆顶元素，然后维护对顶堆；
• $k$ 值 $+1/-1$：根据新的 $k$ 值直接维护对顶堆。

显然，查询第 $k$ 大元素的时间复杂度是 $O(1)$ 的。由于插入、删除或调整 $k$ 值后，小根堆的大小与期望的 $k$ 值最多相差 $1$，故每次维护最多只需对大根堆与小根堆中的元素进行一次调整，因此，这些操作的时间复杂度都是 $O(\log n)$ 的。

参考代码：

#include <cstdio>
#include <iostream>
#include <queue>
using namespace std;

int main() {
  int t, x;
  scanf("%d", &t);
  while (t--) {
    // 大根堆，维护前一半元素（存小值）
    priority_queue<int, vector<int>, less<int> > a;
    // 小根堆，维护后一半元素（存大值）
    priority_queue<int, vector<int>, greater<int> > b;
    while (scanf("%d", &x) && x) {
      // 若为查询并删除操作，输出并删除大根堆堆顶元素
      // 因为这题要求输出中位数中较小者（偶数个数字会存在两个中位数候选）
      // 这个和上面的第k大讲解有稍许出入，但如果理解了上面的，这个稍微变通下便可理清
      if (x == -1) {
        printf("%d\n", a.top());
        a.pop();
      }
      // 若为插入操作，根据大根堆堆顶的元素值，选择合适的堆进行插入
      else {
        if (a.empty() || x <= a.top())
          a.push(x);
        else
          b.push(x);
      }
      // 对对顶堆进行调整
      if (a.size() > (a.size() + b.size() + 1) / 2) {
        b.push(a.top());
        a.pop();
      } else if (a.size() < (a.size() + b.size() + 1) / 2) {
        a.push(b.top());
        b.pop();
      }
    }
  }
  return 0;
}

1|0习题

• SPOJ RMID - Running Median
• 洛谷 P1801 黑匣子

5|0匹配堆

5|1引入

配对堆是一个支持插入，查询/删除最小值，合并，修改元素等操作的数据结构，是一种可并堆。有速度快和结构简单的优势，但由于其为基于势能分析的均摊复杂度，无法可持久化。

5|2定义

配对堆是一棵满足堆性质的带权多叉树（如下图），即每个节点的权值都小于或等于他的所有儿子（以小根堆为例，下同）。

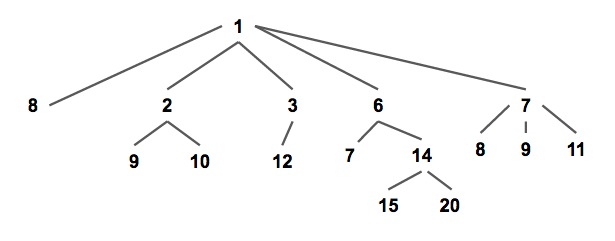
通常我们使用儿子 - 兄弟表示法储存一个配对堆（如下图），一个节点的所有儿子节点形成一个单向链表。每个节点储存第一个儿子的指针，即链表的头节点；和他的右兄弟的指针。

这种方式便于实现配对堆，也将方便复杂度分析。

struct Node {
  T v;  // T为权值类型
  Node *child, *sibling;
  // child 指向该节点第一个儿子，sibling 指向该节点的下一个兄弟。
  // 若该节点没有儿子/下个兄弟则指针指向 nullptr。
};

从定义可以发现，和其他常见的堆结构相比，配对堆不维护任何额外的树大小，深度，排名等信息（二叉堆也不维护额外信息，但它是通过维持一个严格的完全二叉树结构来保证操作的复杂度），且任何一个满足堆性质的树都是一个合法的配对堆，这样简单又高度灵活的数据结构奠定了配对堆在实践中优秀效率的基础；作为对比，斐波那契堆糟糕的常数就是因为它需要维护很多额外的信息。

配对堆通过一套精心设计的操作顺序来保证它的总复杂度，原论文^[1]将其称为「一种自调整的堆（$\text{Self Adjusting Heap}$）」。在这方面和 $\text{Splay}$ 树（在原论文中被称作「$\text{Self Adjusting Binary Tree}$」）颇有相似之处。

5|3过程

1|0查询最小值

从配对堆的定义可看出，配对堆的根节点的权值一定最小，直接返回根节点即可。

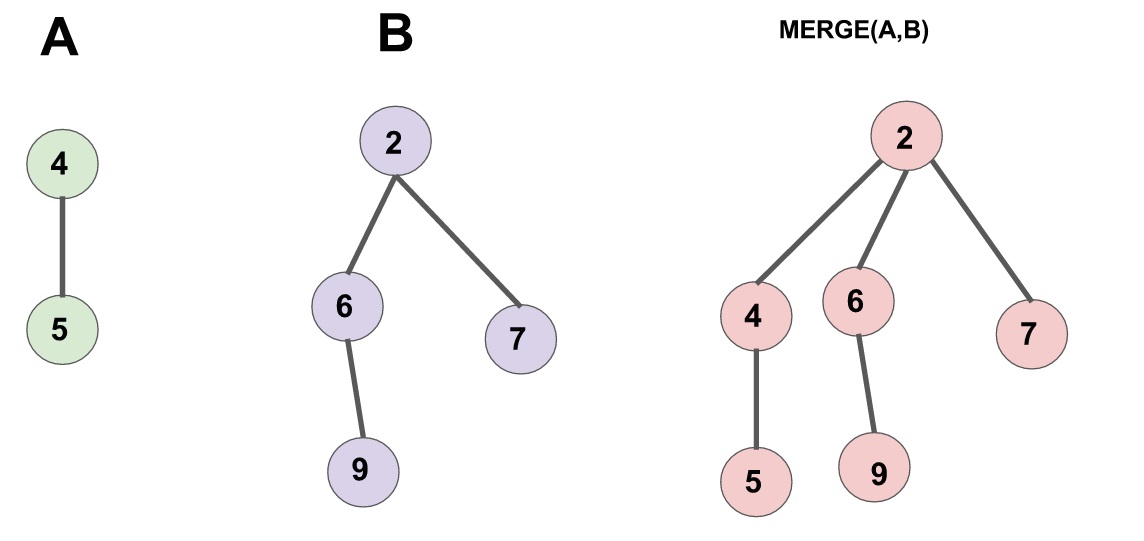
1|0合并

合并两个配对堆的操作很简单，首先令两个根节点较小的一个为新的根节点，然后将较大的根节点作为它的儿子插入进去。（见下图）

需要注意的是，一个节点的儿子链表是按插入时间排序的，即最右边的节点最早成为父节点的儿子，最左边的节点最近成为父节点的儿子。

实现：

Node* meld(Node* x, Node* y) {
  // 若有一个为空则直接返回另一个
  if (x == nullptr) return y;
  if (y == nullptr) return x;
  if (x->v > y->v) std::swap(x, y);  // swap后x为权值小的堆，y为权值大的堆
  // 将y设为x的儿子
  y->sibling = x->child;
  x->child = y;
  return x;  // 新的根节点为 x
}

1|0插入

合并都有了，插入就直接把新元素视为一个新的配对堆和原堆合并就行了。

1|0删除最小值

首先要提及的一点是，上文的几个操作都十分偷懒，完全没有对数据结构进行维护，所以我们需要小心设计删除最小值的操作，来保证总复杂度不出问题。

根节点即为最小值，所以要删除的是根节点。考虑拿掉根节点之后会发生什么：根节点原来的所有儿子构成了一片森林；而配对堆应当是一棵树，所以我们需要通过某种顺序把这些儿子全部合并起来。

一个很自然的想法是使用 meld 函数把儿子们从左到右挨个并在一起，这样做的话正确性是显然的，但是会导致单次操作复杂度退化到 $O(n)$。

为了保证总的均摊复杂度，需要使用一个「两步走」的合并方法：

1. 把儿子们两两配成一对，用 meld 操作把被配成同一对的两个儿子合并到一起（见下图 1），
2. 将新产生的堆 从右往左（即老的儿子到新的儿子的方向）挨个合并在一起（见下图 2）。

先实现一个辅助函数 merges，作用是合并一个节点的所有兄弟。

实现：

Node* merges(Node* x) {
  if (x == nullptr || x->sibling == nullptr)
    return x;  // 如果该树为空或他没有下一个兄弟，就不需要合并了，return。
  Node* y = x->sibling;                // y 为 x 的下一个兄弟
  Node* c = y->sibling;                // c 是再下一个兄弟
  x->sibling = y->sibling = nullptr;   // 拆散
  return meld(merges(c), meld(x, y));  // 核心部分
}

最后一句话是该函数的核心，这句话分三部分：

1. meld(x,y)「配对」了 $x$ 和 $y$。
2. merges(c) 递归合并 $c$ 和他的兄弟们。
3. 将上面 $2$ 个操作产生的 $2$ 个新树合并。

需要注意到的是，上文提到了第二步时的合并方向是有要求的（从右往左合并），该递归函数的实现已保证了这个顺序，如果读者需要自行实现迭代版本的话请务必注意保证该顺序，否则复杂度将失去保证。

有了 merges 函数，delete-min 操作就显然了。

实现：

Node* delete_min(Node* x) {
  Node* t = merges(x->child);
  delete x;  // 如果需要内存回收
  return t;
}

1|0减小一个元素的值

要实现这个操作，需要给节点添加一个「父」指针，当节点有左兄弟时，其指向左兄弟而非实际的父节点；否则，指向其父节点。

首先节点的定义修改为：

实现：

struct Node {
  LL v;
  int id;
  Node *child, *sibling;
  Node *father;  // 新增：父指针，若该节点为根节点则指向空节点 nullptr
};

meld 操作修改为：

实现：

Node* meld(Node* x, Node* y) {
  if (x == nullptr) return y;
  if (y == nullptr) return x;
  if (x->v > y->v) std::swap(x, y);
  if (x->child != nullptr) {  // 新增：维护父指针
    x->child->father = y;
  }
  y->sibling = x->child;
  y->father = x;  // 新增：维护父指针
  x->child = y;
  return x;
}

merges 操作修改为：

实现：

Node *merges(Node *x) {
  if (x == nullptr) return nullptr;
  x->father = nullptr;  // 新增：维护父指针
  if (x->sibling == nullptr) return x;
  Node *y = x->sibling, *c = y->sibling;
  y->father = nullptr;  // 新增：维护父指针
  x->sibling = y->sibling = nullptr;
  return meld(merges(c), meld(x, y));
}

现在我们来考虑如何实现 decrease-key 操作。
首先我们发现，当我们减少节点 x 的权值之后，以 x 为根的子树仍然满足配对堆性质，但 x 的父亲和 x 之间可能不再满足堆性质。
因此我们把整棵以 x 为根的子树剖出来，现在两棵树都符合配对堆性质了，然后把他们合并起来，就完成了全部操作。

实现：

// root为堆的根，x为要操作的节点，v为新的权值，调用时需保证 v <= x->v
// 返回值为新的根节点
Node *decrease_key(Node *root, Node *x, LL v) {
  x->v = v;                 // 更新权值
  if (x == root) return x;  // 如果 x 为根，则直接返回
  // 把x从fa的子节点中剖出去，这里要分x的位置讨论一下。
  if (x->father->child == x) {
    x->father->child = x->sibling;
  } else {
    x->father->sibling = x->sibling;
  }
  if (x->sibling != nullptr) {
    x->sibling->father = x->father;
  }
  x->sibling = nullptr;
  x->father = nullptr;
  return meld(root, x);  // 重新合并 x 和根节点
}

5|4复杂度分析

配对堆结构与实现简单，但时间复杂度分析并不容易。

原论文${}^1$仅将复杂度分析到 meld 和 delete-min 操作均为均摊 $O(\log n)$，但提出猜想认为其各操作都有和斐波那契堆相同的复杂度。

遗憾的是，后续发现，不维护额外信息的配对堆，在特定的操作序列下，decrease-key 操作的均摊复杂度下界至少为 $\mathrm{\Omega }(\log \log n{)}^2$。

目前对复杂度上界比较好的估计有，Iacono 的 $O(1)$ meld，$O(\log n)$ decrease-key${}^3$；Pettie 的 $O(2^{2\sqrt{\log \log n}})$ meld 和 decrease-key${}^4$。需要注意的是，前述复杂度均为均摊复杂度，因此不能对各结果分别取最小值。

5|5参考文献

• https://en.wikipedia.org/wiki/Pairing_heap
• https://brilliant.org/wiki/pairing-heap/

6|0set

set 是关联容器，含有键值类型对象的已排序集，搜索、移除和插入拥有对数复杂度。set 内部通常采用红黑树实现。平衡二叉树的特性使得 set 非常适合处理需要同时兼顾查找、插入与删除的情况。

和数学中的集合相似，set 中不会出现值相同的元素。如果需要有相同元素的集合，需要使用 multiset。multiset 的使用方法与 set 的使用方法基本相同。

6|1插入与删除操作

• insert(x) 当容器中没有等价元素的时候，将元素 x 插入到 set 中。
• erase(x) 删除值为 x 的 所有 元素，返回删除元素的个数。
• erase(pos) 删除迭代器为 pos 的元素，要求迭代器必须合法。
• erase(first,last) 删除迭代器在 $[first,last)$ 范围内的所有元素。
• clear() 清空 set。

$\text{insert}$ 函数的返回值：

$\text{insert}$ 函数的返回值类型为 pair<iterator, bool>，其中 $\text{iterator}$ 是一个指向所插入元素（或者是指向等于所插入值的原本就在容器中的元素）的迭代器，而 $\text{bool}$ 则代表元素是否插入成功，由于 set 中的元素具有唯一性质，所以如果在 set 中已有等值元素，则插入会失败，返回 $\text{false}$，否则插入成功，返回 $\text{true}$；map 中的 $\text{insert}$ 也是如此。

6|2迭代器

set 提供了以下几种迭代器：

1. begin()/cbegin()
   返回指向首元素的迭代器，其中 *begin = front。
2. end()/cend()
   返回指向数组尾端占位符的迭代器，注意是没有元素的。
3. rbegin()/crbegin()
   返回指向逆向数组的首元素的逆向迭代器，可以理解为正向容器的末元素。
4. rend()/crend()
   返回指向逆向数组末元素后一位置的迭代器，对应容器首的前一个位置，没有元素。

以上列出的迭代器中，含有字符 c 的为只读迭代器，你不能通过只读迭代器去修改 set 中的元素的值。如果一个 set 本身就是只读的，那么它的一般迭代器和只读迭代器完全等价。只读迭代器自 $\text{C++11}$ 开始支持。

6|3查找操作

• count(x) 返回 set 内键为 $x$ 的元素数量。
• find(x) 在 set 内存在键为 $x$ 的元素时会返回该元素的迭代器，否则返回 end()。
• lower_bound(x) 返回指向首个不小于给定键的元素的迭代器。如果不存在这样的元素，返回 end()。
• upper_bound(x) 返回指向首个大于给定键的元素的迭代器。如果不存在这样的元素，返回 end()。
• empty() 返回容器是否为空。
• size() 返回容器内元素个数。

lower_bound 和 upper_bound 的时间复杂度：

set 自带的 lower_bound 和 upper_bound 的时间复杂度为 $O(\log n)$。

但使用 algorithm 库中的 lower_bound 和 upper_bound 函数对 set 中的元素进行查询，时间复杂度为 $O(n)$。

nth_element 的时间复杂度 ：

set 没有提供自带的 nth_element。使用 algorithm 库中的 nth_element 查找第 $k$ 大的元素时间复杂度为 $O(n)$。

如果需要实现平衡二叉树所具备的 $O(\log n)$ 查找第 $k$ 大元素的功能，需要自己手写平衡二叉树或权值线段树，或者选择使用 $\text{pb\_ds}$ 库中的平衡二叉树。

6|4使用样例

1|0set 在贪心中的使用

在贪心算法中经常会需要出现类似 找出并删除最小的大于等于某个值的元素。这种操作能轻松地通过 set 来完成。

// 现存可用的元素
set<int> available;
// 需要大于等于的值
int x;

// 查找最小的大于等于x的元素
set<int>::iterator it = available.lower_bound(x);
if (it == available.end()) {
  // 不存在这样的元素，则进行相应操作……
} else {
  // 找到了这样的元素，将其从现存可用元素中移除
  available.erase(it);
  // 进行相应操作……
}

7|0map

map 是有序键值对容器，它的元素的键是唯一的。搜索、移除和插入操作拥有对数复杂度。map 通常实现为红黑树。

设想如下场景：现在需要存储一些键值对，例如存储学生姓名对应的分数：Tom 0，Bob 100，Alan 100。但是由于数组下标只能为非负整数，所以无法用姓名作为下标来存储，这个时候最简单的办法就是使用 $\text{STL}$ 中的 map。

map 重载了 operator[]，可以用任意定义了 operator < 的类型作为下标（在 map 中叫做 key，也就是索引）：

map<Key, T> yourMap;

其中，Key 是键的类型，T 是值的类型，下面是使用 map 的实例：

map<string, int> mp;

map 中不会存在键相同的元素，multimap 中允许多个元素拥有同一键。multimap 的使用方法与 map 的使用方法基本相同。

正是因为 multimap 允许多个元素拥有同一键的特点，multimap 并没有提供给出键访问其对应值的方法。

1|0插入与删除操作

• 可以直接通过下标访问来进行查询或插入操作。例如 mp["Alan"]=100。
• 通过向 map 中插入一个类型为 pair<Key, T> 的值可以达到插入元素的目的，例如 mp.insert(pair<string,int>("Alan",100));；
• erase(key) 函数会删除键为 key 的 所有 元素。返回值为删除元素的数量。
• erase(pos): 删除迭代器为 pos 的元素，要求迭代器必须合法。
• erase(first,last): 删除迭代器在 $[first,last)$ 范围内的所有元素。
• clear() 函数会清空整个容器。

下标访问中的注意事项：

在利用下标访问 map 中的某个元素时，如果 map 中不存在相应键的元素，会自动在 map 中插入一个新元素，并将其值设置为默认值（对于整数，值为零；对于有默认构造函数的类型，会调用默认构造函数进行初始化）。

当下标访问操作过于频繁时，容器中会出现大量无意义元素，影响 map 的效率。因此一般情况下推荐使用 find() 函数来寻找特定键的元素。

7|1查询操作

• count(x): 返回容器内键为 x 的元素数量。复杂度为 $O(\log (size)+ans)$（关于容器大小对数复杂度，加上匹配个数）。
• find(x): 若容器内存在键为 x 的元素，会返回该元素的迭代器；否则返回 end()。
• lower_bound(x): 返回指向首个不小于给定键的元素的迭代器。
• upper_bound(x): 返回指向首个大于给定键的元素的迭代器。若容器内所有元素均小于或等于给定键，返回 end()。
• empty(): 返回容器是否为空。
• size(): 返回容器内元素个数。

7|2使用样例

1|0map 用于存储复杂状态

在搜索中，我们有时需要存储一些较为复杂的状态（如坐标，无法离散化的数值，字符串等）以及与之有关的答案（如到达此状态的最小步数）。map 可以用来实现此功能。其中的键是状态，而值是与之相关的答案。下面的示例展示了如何使用 map 存储以 string 表示的状态。

// 存储状态与对应的答案
map<string, int> record;

// 新搜索到的状态与对应答案
string status;
int ans;
// 查找对应的状态是否出现过
map<string, int>::iterator it = record.find(status);
if (it == record.end()) {
  // 尚未搜索过该状态，将其加入状态记录中
  record[status] = ans;
  // 进行相应操作……
} else {
  // 已经搜索过该状态，进行相应操作……
}

7|3遍历容器

可以利用迭代器来遍历关联式容器的所有元素。

set<int> s;
typedef set<int>::iterator si;
for (si it = s.begin(); it != s.end(); it++) cout << *it << endl;

需要注意的是，对 map 的迭代器解引用后，得到的是类型为 pair<Key, T> 的键值对。

在 $\text{C++11}$ 中，使用范围 $\text{for}$ 循环会让代码简洁很多：

set<int> s;
for (auto x : s) cout << x << endl;

对于任意关联式容器，使用迭代器遍历容器的时间复杂度均为 $O(n)$。

7|4自定义比较方式

set 在默认情况下的比较函数为 <（如果是非内置类型需要重载 < 运算符）。然而在某些特殊情况下，我们希望能自定义 set 内部的比较方式。

这时候可以通过传入自定义比较器来解决问题。

具体来说，我们需要定义一个类，并在这个类中重载 () 运算符。

例如，我们想要维护一个存储整数，且较大值靠前的 set，可以这样实现：

struct cmp {
  bool operator()(int a, int b) { return a > b; }
};

set<int, cmp> s;

对于其他关联式容器，可以用类似的方式实现自定义比较，这里不再赘述。

---

1. The pairing heap: a new form of self-adjusting heap ↩︎

__EOF__

本文作者：So_noSlack
本文链接：https://www.cnblogs.com/So-noSlack/p/18302382.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！