AT_abc178_d 题解

合集 - 题解(26)

1.AT_abc180_d 题解2023-07-242.SP12304 题解2023-07-213.AT_abc218_d 题解2023-07-244.AT_abc215_d 题解2023-07-245.AT_abc246_d 题解2023-07-246.AT_arc149_a 题解2023-07-267.AT_agc017_b 题解2023-07-268.AT_arc154_b 题解2023-07-269.AT_arc041_b 题解2023-07-26

10.AT_abc178_d 题解2023-07-26

11.AT_abc182_d 题解2023-07-2712.AT_arc113_c 题解2023-07-2713.CF709B 题解2023-07-2814.AT_tenka1_2015_qualB_b 题解2023-07-2815.AT_agc022_a 题解2023-07-2916.CF858C 题解2023-07-2917.CF1204A 题解2023-08-0218.CF1359A 题解2023-08-0219.CF1363A 题解2023-08-0220.CF1282A 题解2023-08-0221.CF479C 题解2023-08-0222.CF1468N 题解2023-08-0223.CF452C 题解2023-08-1324.P2427 题解2023-09-2825.AT_agc019_b 题解2023-09-2826.AT_arc111_a 题解2023-09-28

收起

洛谷链接&Atcoder 链接

本篇题解为此题较简单做法及较少码量，并且码风优良，请放心阅读。

1|0题目简述

给定一个正整数 $S$，问有多少个数满足以下条件：

• 序列中必须为 $\ge 3$ 的正整数。
• 序列中的和必须为 $S$。

2|0思路

首先想到组合数学，本题可通过组合数学插板法解决。

引入：例题，求 $n$ 个苹果分为 $k$ 组的方案数，每组苹果个数仅需 $\ge 1$。

那么这道题就可转化为：

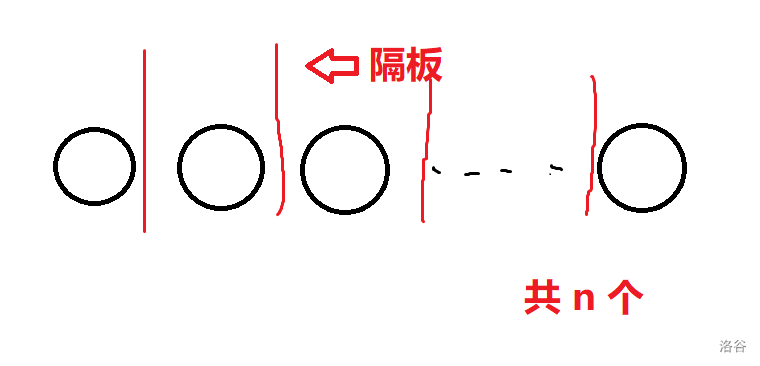
如图，共有 $n$ 个苹果用 $k-1$ 个隔板隔开 $k$ 组，即从 $n-1$ 个空中选 $k-1$ 个空插隔板，所以答案即为 $C_{n-1}^{k-1}$。

注意：隔板不能重合也不能在两边，因为每组苹果个数需 $\ge 1$。

现在再来看此题，发现每组需 $\ge 3$ 且组数不确定，所以需要枚举组数 $i$ 从 $1$ 到 $n/3$，并且空格数即可插板的位置数也会发生变化：

$$n-1\to n-2\times i-1$$

隔板数依然不变，是 $i-1$。所以对于此题，方案数即为 $C_{n-2\times i-1}^{i-1}$。

接下来就需要解决组合数的计算了，因为此题的数据范围不大，所以就可以用杨辉三角预处理组合数。学过组合数的同学应该都学过，这里直接说结论：杨辉三角的第 $n$ 行的第 $i$ 个数即为 $C_n^i$ 的值。

预处理如下（预处理过程中也要模 $1000000007$）：

for(int i = 0; i <= n; i ++) {
		C[i][0] = C[i][j] = 1;
		for(int j = 1; j < i; j ++) 
			C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % MOD;
	}

经过以上分析及部分代码讲解，基本的代码框架就很清晰了，下面是具体代码实现：

#include<iostream>
using namespace std;
#define MOD 1000000007

int S, C[2005][2005]; // 组合数数组
long long ans = 0; // 记录答案，可不开 long long

int main() {
	cin >> S;
	for(int i = 0; i <= S; i ++) {
		C[i][0] = C[i][j] = 1;
		for(int j = 1; j < i; j ++) 
			C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % MOD; // 杨辉三角预处理组合数
	}
        // 枚举组数
	for(int i = 1; i <= S / 3; i ++) 
		ans = (ans + C[S - 2 * i - 1][i - 1]) % MOD; // 累计答案
        cout << ans << endl; // 输出答案，换行好习惯 
	return 0;
}

提交记录：

$$\text{The End!}$$

__EOF__

本文作者：So_noSlack
本文链接：https://www.cnblogs.com/So-noSlack/p/17583208.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！