第十五节 数论 - 2
AT_agc017_b 题解
本篇题解为此题较简单做法,请放心阅读。
题目简述
一共有 \(n\) 个格子,给定两个整数 \(A,B\) 分别位于第 \(1\) 和第 \(n\) 格,中间有 \(n−2\) 个空格。询问是否存在一种填数方案满足任意相邻两个数之差的绝对值在 \([C,D]\) 之间。
依次输入 \(n,a,b,c,d\)。
若能,输出 YES;反之输出 NO。
思路
遇事不决先看数据范围,发现数据范围 \(3 \le N \le 5 \times 10^5\),那么时间复杂度在 \(O(N)\) 以内就可以接受,本篇题解就详细解释一下 \(O(N)\) 的算法。
首先可以想到 \(O(N)\) 的复杂度就是遍历 \(N\),可以想到枚举在 \(A,B\) 之间填了 \(i\) 个数,从 \(0 \sim N-2\) 遍历即可,遍历时进行判断,如果满足要求可直接输出 YES,否则遍历完后输出 NO。
接着可以先把区间 \([C,D]\) 转化为区间 \([0,D-C]\),那么判断条件就需要判断 \(C\) 的合法性及可行性:
接着可写出判断条件的边界条件,首先是最大值即右区间,通过右区间 \(D-C\) 很容易得出:
以及左区间:
如果合法的 \(C\) 在此区间内则输出 YES,否则在遍历后输出 NO。
注意:因为均为闭区间,所以需是 \(\le\) 而不是 \(<\)。
经过以上分析及转化,很容易即可得出代码了。
AT_arc154_b 题解
本篇题解为此题较简单做法及较少码量,并且码风优良,请放心阅读。
题目简述
给定两个长度为 \(n\) 的字符串 \(S,T\),定义一次操作可取出 \(S\) 的首位,插到 \(S\) 的任意位置。
求最少的操作次数使 \(S\) 变成 \(T\),无解输出 -1。
思路
首先很容易想到如果 \(S\) 和 \(T\) 的某个字母的个数不同,那么 \(S\) 不可能变为 \(T\)。因为不可能凭空变出一个字母。通过两个桶数组即可记录 \(S,T\) 的每个字母个数:
int cnt_s[30], cnt_t[30];
for(int i = 0; i < n; i ++)
cnt_s[s[i] - 'a'] ++, cnt_t[t[i] - 'a'] ++;
接着验证 \(S\) 和 \(T\) 的各个字母数量是否一致,一旦不一致立刻输出 -1 即可:
for(int i = 0; i < 26; i ++)
if(cnt_s[i] != cnt_t[i]) {
cout << "-1\n";
return 0;
}
特判 -1 的情况后就很简单了,仅需遍历 \(T\) 即可,在过程中如果 \(S\) 的当前位与 \(T\) 相同,则表示不必进行操作,把之前记录的 \(ans\) 自减即可。
经过以上分析,很容易即可得出完整代码了:
#include<iostream>
using namespace std;
int n, cnt_s[30], cnt_t[30], ans = 0; // 必要数组不解释
string s, t; // 模式串和匹配串
int main() {
cin >> n >> s >> t;
ans = n - 1; // 因为下标从 0 开始,所以 ans 需初始化为 n - 1
for(int i = 0; i < n; i ++) cnt_s[s[i] - 'a'] ++, cnt_t[t[i] - 'a'] ++; // 统计字母个数
for(int i = 0; i < 26; i ++)
if(cnt_s[i] != cnt_t[i]) {
cout << "-1\n"; // 字母个数不相同直接输出
return 0;
}
for(int i = n - 1; i >= 0; i --)
if(s[ans] == t[i]) ans --; // 满足条件不必操作,ans --
cout << ans + 1 << endl; // 还是下标问题答案需 +1,建议写下标从 1 开始的
return 0;
}
AT_arc041_b 题解
本篇题解为此题较简单做法及较少码量,并且码风优良,请放心阅读。
题目简述
给定一个 \(N \times M\) 的矩阵,此矩阵的每一个元素都向上、下、左、右 \(4\) 个方向同时扩散(原来的位置不保留)。
现给出原矩阵扩散后的矩阵,求原矩阵。
思路
对于扩散后的 \((i,j)\),是原矩阵的 \((i-1,j)\),\((i+1,j)\),\((i,j-1)\),\((i,j+1)\) 扩散而来的,那么就可以通过这 \(4\) 个点推断出原矩阵上 \((i,j)\) 的数。
例如:
010
101
010
这个样例中,只有 \((2,2)\) 周围 \(4\) 个方向都是非 \(0\) 数,所以从这个例子中就可推出计算原矩阵上 \((i,j)\) 的数的方程式了:
那么就会产生一个疑问,对于边界有没有特殊情况?比如对于 \((1,1)\) 他的方程式带入就为:
所以对于边界 \((0,1)\) 和 \((1,0)\) 的初始化就尤为重要,这里建议初始化为 \(0\),这样取 \(\min\) 之后就为 \(0\) 了。
处理完边界的初始化之后基本就没什么了,不过我们还是要思考一下,比如对于以下情况:
0000000
0001000
0030400
0209030
0050600
0003000
0000000
\((2,3)\) 并不是边界并且也不满足四周都是非 \(0\) 数,那么它是不是一种特殊情况?会不会不满足上面推出的方程式?答案是肯定的,因为 \((2,3)\) 的上、左两个方向的数是 \(0\),则取 \(\min\) 之后就一定为 \(0\) 了。
经过以上分析以及一些证明,基本就有大致的代码框架了:
#include<iostream>
using namespace std;
int n, m, mp[505][505]; // mp 记录地图
char c; // 临时储存
int main() {
cin >> n >> m;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= m; j ++) {
cin >> c;
mp[i][j] = c - '0'; // 转化为数字
}
for(int i = 1; i <= n; i ++) {
for(int j = 1; j <= m; j ++) {
int minn = min(min(mp[i - 1][j], mp[i + 1][j]), min(mp[i][j - 1], mp[i][j + 1])); // 计算 minn 值
cout << minn; // 可直接输出
// 把周围扩散的数减去
mp[i - 1][j] -= minn; mp[i + 1][j] -= minn;
mp[i][j - 1] -= minn; mp[i][j + 1] -= minn;
}
cout << endl; // 记得换行
}
return 0;
}
AT_abc178_d 题解
本篇题解为此题较简单做法及较少码量,并且码风优良,请放心阅读。
题目简述
给定一个正整数 \(S\),问有多少个数满足以下条件:
- 序列中必须为 \(\ge 3\) 的正整数。
- 序列中的和必须为 \(S\)。
思路
首先想到组合数学,本题可通过组合数学插板法解决。
引入:例题,求 \(n\) 个苹果分为 \(k\) 组的方案数,每组苹果个数仅需 \(\ge 1\)。
那么这道题就可转化为:
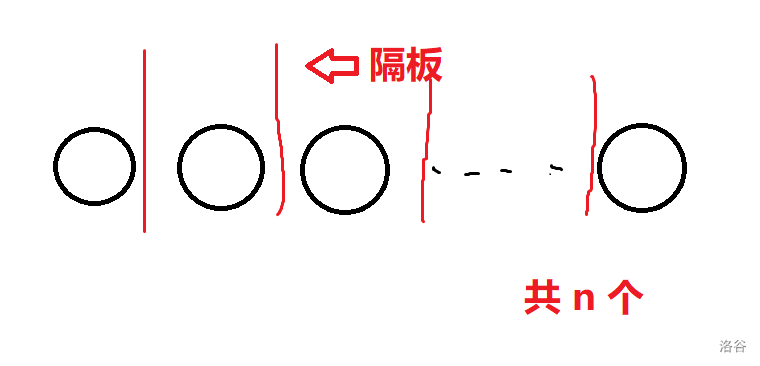
如图,共有 \(n\) 个苹果用 \(k-1\) 个隔板隔开 \(k\) 组,即从 \(n-1\) 个空中选 \(k-1\) 个空插隔板,所以答案即为 \(C_{n-1}^{k-1}\)。
注意:隔板不能重合也不能在两边,因为每组苹果个数需 \(\ge 1\)。
现在再来看此题,发现每组需 \(\ge 3\) 且组数不确定,所以需要枚举组数 \(i\) 从 \(1\) 到 \(n/3\),并且空格数即可插板的位置数也会发生变化:
隔板数依然不变,是 \(i-1\)。所以对于此题,方案数即为 \(C_{n-2 \times i-1}^{i-1}\)。
接下来就需要解决组合数的计算了,因为此题的数据范围不大,所以就可以用杨辉三角预处理组合数。学过组合数的同学应该都学过,这里直接说结论:杨辉三角的第 \(n\) 行的第 \(i\) 个数即为 \(C_n^i\) 的值。
预处理如下(预处理过程中也要模 \(1000000007\)):
for(int i = 0; i <= n; i ++) {
C[i][0] = C[i][j] = 1;
for(int j = 1; j < i; j ++)
C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % MOD;
}
经过以上分析及部分代码讲解,基本的代码框架就很清晰了,下面是具体代码实现:
#include<iostream>
using namespace std;
#define MOD 1000000007
int S, C[2005][2005]; // 组合数数组
long long ans = 0; // 记录答案,可不开 long long
int main() {
cin >> S;
for(int i = 0; i <= S; i ++) {
C[i][0] = C[i][j] = 1;
for(int j = 1; j < i; j ++)
C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % MOD; // 杨辉三角预处理组合数
}
// 枚举组数
for(int i = 1; i <= S / 3; i ++)
ans = (ans + C[S - 2 * i - 1][i - 1]) % MOD; // 累计答案
cout << ans << endl; // 输出答案,换行好习惯
return 0;
}
提交记录:
A. 循环与非
题目描述
给定长度为 \(n\) 的序列 {\(a_n\)},每一个数字都不超过 \(2\) 的 \(k\) 次方。给定 \(m\) 次操作,每次操作形如:
0 x y :将 \(a[x]\) 改为 \(y\)。
1 x y :令 \(t=y\) NAND \(a[0]\) NAND \(a[1]\) NAND \(a[2]\) NAND ... NAND \(a[i\) \(mod\) \(n]\) NAND ... NAND \(a[(x*n-1)\) \(mod\) \(n]\)。
NAND 代表按位与非操作。
求所有计算结果的 \(t\) 的异或和。
输入格式
第一行包含三个正整数 \(n,m,k\)。
接下来一行 \(n\) 个整数 \(a_0 \sim a_{n-1}\)。
接下来 \(m\) 行每行三个整数 \(op,x,y\)。
输出格式
输出一行一个整数表示答案。
样例输入
2 3 3
1 2
1 2 3
0 0 3
1 2 2
样例输出
2
样例输入
7 4 4
4 6 4 7 10 9 11
1 5 7
1 7 14
0 6 7
1 6 5
样例输出
9
数据规模
\(1 \le n,m \le 10^4\),\(0 \le y < 2^k\)
操作 \(0\) 中,\(0 \le x < n\)
操作 \(1\) 中,\(1 \le x < 10^9\)
\(1 \le k \le 30\)
点击查看代码
#include<iostream>
#include<set>
using namespace std;
int m, n, k, a[10005];
set<int> st[30];
int find(int i) { return st[i].empty() ? -1 : *st[i].rbegin(); }
int main() {
cin >> n >> m >> k;
int tmp;
for(int i = 0; i < n; i ++) {
cin >> tmp;
for(int j = 0; j < k; j ++)
if(!(tmp & 1 << j)) st[j].insert(i);
}
int opt, x, y, res, t = 0, last;
while(m --) {
cin >> opt >> x >> y;
if(opt == 0)
for(int i = 0; i < k; i ++)
if(!(y & 1 << i)) st[i].insert(x);
else st[i].erase(x);
else {
res = 0;
for(int i = 0; i < k; i ++){
last = find(i);
if(last == -1) res += (1ll * x * n + (y >> i & 1) & 1) << i;
else res += (n - last & 1) << i;
}
t ^= res;
}
}
cout << t;
return 0;
}
编译结果
compiled successfully
time: 100ms, memory: 7232kb, score: 100, status: Accepted
> test 1: time: 1ms, memory: 3408kb, points: 10, status: Accepted
> test 2: time: 5ms, memory: 3448kb, points: 10, status: Accepted
> test 3: time: 25ms, memory: 7232kb, points: 10, status: Accepted
> test 4: time: 3ms, memory: 4076kb, points: 10, status: Accepted
> test 5: time: 17ms, memory: 5248kb, points: 10, status: Accepted
> test 6: time: 2ms, memory: 3544kb, points: 10, status: Accepted
> test 7: time: 10ms, memory: 3720kb, points: 10, status: Accepted
> test 8: time: 10ms, memory: 3604kb, points: 10, status: Accepted
> test 9: time: 18ms, memory: 4716kb, points: 10, status: Accepted
> test 10: time: 9ms, memory: 3476kb, points: 10, status: Accepted
B. 蹦蹦萝卜
题目描述
有一个环状的操场,操场被分割为 \(n\) 个小块,每个小块上写着一个数字。
有一只小白兔站在操场的起点 \(1\),它每次可以跳 \(k\) 个小块,然后拿走等同于它跳之前所站小块上数字数量的胡萝卜,问它跳 \(m\) 次,总共可以拿到几个胡萝卜?
小白兔在 \(i\) 处时,它跳到的下一个位置是 \((i+k)\) \(mod\) \(n + 1\)。
如果能够算出来的话,小白兔就能把所有的胡萝卜都带回家吃啦!
答案对 \(10^9+7\) 取模。
输入格式
第一行包含两个正整数 \(n\) 和 \(k\),
第二行 \(n\) 个正整数 \(a_1...a_n\) 每个小块上的数字,
第三行一个正整数 \(m\)。
输出格式
输出一行一个整数表示答案。
样例输入
5 1
1 10 100 1000 10000
3
样例输出
10101
数据规模
\(1 \le k \le n \le 10^6\),\(1 \le a_i \le 10^6\), \(1 \le m \le 10^{18}\)
点击查看代码
#include<iostream>
#include<set>
using namespace std;
#define MOD 1000000007
int n, k, a[1000005], p[1000005][70], c[1000005][70];
long long m;
int main() {
cin >> n >> k;
for(int i = 1; i <= n; i ++) cin >> a[i];
cin >> m;
for(int i = 1; i <= n; i ++) {
p[i][0] = (i + k) % n + 1;
c[i][0] = a[i];
}
for(int j = 1; j <= 60; j ++) {
for(int i = 1; i <= n; i ++) {
p[i][j] = p[p[i][j - 1]][j - 1];
c[i][j] = (c[i][j - 1] + c[p[i][j - 1]][j - 1]) % MOD;
}
}
long long res = 0;
int x = 1;
for(int j = 0; j < 63; j ++) {
if(m & 1LL << j) {
res += c[x][j];
x = p[x][j];
}
}
cout << res % MOD << endl;
return 0;
}
编译结果
compiled successfully
time: 12253ms, memory: 496952kb, score: 100, status: Accepted
> test 1: time: 1775ms, memory: 386052kb, points: 10, status: Accepted
> test 2: time: 106ms, memory: 58732kb, points: 10, status: Accepted
> test 3: time: 1147ms, memory: 262252kb, points: 10, status: Accepted
> test 4: time: 324ms, memory: 116136kb, points: 10, status: Accepted
> test 5: time: 1937ms, memory: 410032kb, points: 10, status: Accepted
> test 6: time: 273ms, memory: 99752kb, points: 10, status: Accepted
> test 7: time: 2433ms, memory: 496952kb, points: 10, status: Accepted
> test 8: time: 1629ms, memory: 360016kb, points: 10, status: Accepted
> test 9: time: 1412ms, memory: 313324kb, points: 10, status: Accepted
> test 10: time: 1217ms, memory: 275484kb, points: 10, status: Accepted
C. 超大范围幂运算
时间:1s 空间:256M
题目描述
有 \(3\) 个整数 \(a, b, c\),求 \(a^b\) \(mod\) \(c\)
输入格式
第一行包含一个整数 \(T\),表示测试数据组数。
对于每组测试数据,包含 \(3\) 个整数 \(a, b, c\)。
输出格式
对于每组测试数据,输出一个整数表示答案。
样例1输入
6
0 0 1
0 0 100
2 5 17
0 10 100
100 0 1000000000000000000
114 514 1919810
样例1输出
0
1
15
0
1
290606
约定与提示
对于 \(100\%\) 的数据,\(1 \le T \le 5000\),\(0 \le a,b \le 10^{18}\); \(1 \le c \le 10^{18}\)
点击查看代码
#include<iostream>
#include<set>
using namespace std;
long long T, a, b, c;
long long qadd(long long a, long long b, long long p) {
long long res = 0;
while(b) {
if(b & 1) res = (res + a) % p;
a = (a + a) % p;
b >>= 1;
}
return res;
}
long long quickpow(long long x, long long n, long long m){
if(n == 0) return 1 % m;
long long res = quickpow(qadd(x, x, m), n / 2, m);
if(n & 1) res = qadd(res, x, m);
return res;
}
int main() {
cin >> T;
while(T --) {
cin >> a >> b >> c;
printf("%lld\n", quickpow(a, b, c));
}
return 0;
}
编译结果
compiled successfully
time: 597ms, memory: 3524kb, score: 100, status: Accepted
> test 1: time: 1ms, memory: 3424kb, points: 0, status: Accepted
> test 2: time: 1ms, memory: 3524kb, points: 20, status: Accepted
> test 3: time: 1ms, memory: 3492kb, points: 20, status: Accepted
> test 4: time: 50ms, memory: 3484kb, points: 20, status: Accepted
> test 5: time: 67ms, memory: 3476kb, points: 20, status: Accepted
> test 6: time: 477ms, memory: 3496kb, points: 20, status: Accepted
本文来自博客园,作者:So_noSlack,转载请注明原文链接:https://www.cnblogs.com/So-noSlack/p/17582271.html


