第十三节小组学习

合集 - 2023 暑假杭州站(18)

1.第一节线性数据结构 STL2023-07-10 2.第二节贪心2023-07-11 3.第三节二分2023-07-12 4.第四节小组学习2023-07-13 5.第五节搜索专题 - 12023-07-14 6.第六节搜索专题 - 22023-07-15 7.第七节搜索专题 - 32023-07-17 8.第八节小组学习2023-07-18 9.第九节动态规划 - 12023-07-19 10.第十节动态规划 - 22023-07-20 11.第十一节动态规划 - 32023-07-21 12.第十二节动态规划 - 42023-07-24

13.第十三节小组学习2023-07-24

14.第十四节数论 - 12023-07-25 15.第十五节数论 - 22023-07-26 16.第十六节图论 - 12023-07-27 17.第十七节图论 - 22023-07-28 18.第十八节小组学习2023-07-29

1|0AT_abc180_d 题解

洛谷链接&Atcoder 链接

本篇题解为此题较简单做法及较少码量，并且码风优良，请放心阅读。

2|0题目简述

现有 $S T R$ 和 $E X P$ 两个变量，初始化分别为 $X$ 和 $0$ ，可对变量 $S T R$ 做以下两种操作：

将 $S T R$ 乘 $A$ ，并将 $E X P$ 自加 $1$ 。
将 $S T R$ 加上 $B$ ，并将 $E X P$ 自加 $1$ 。

在 $S T R < Y$ 的情况下，求 $E X P$ 的最大值。

3|0思路

本蒟蒻读完题目后：“贪心!”

那么贪心该怎么贪？通过题意我们很容易想到，无论是执行第一个造作还是第二个操作对 $E X P$ 的影响不变，故就需要我们衡量操作一或二的优势。

如执行操作一比执行操作二更优，则有：

S T R \times A < S T R + B

同时需满足：

S T R \times A < Y

而自信提交的我结果就可想而知了，重新看了一遍题目，发现数据范围： $1 \leq X < Y \leq 10^{18}$ ， $2 \leq A \leq 10$ ， $1 \leq B \leq 10^{9}$ 。

那么 $S T R \times A$ 就有爆 $long long$ 的可能，通过简单的不等式移项可变化为：

S T R < Y / A

这样操作一比操作二更优的情况就解决了。又因为贪心思想，当操作二更优时可直接计算还可加多少 $B$ ，直接加到 $a n s$ 里即可，因为此时再进行操作一必定超过 $Y$ 或 $S T R \times A \geq S T R + B$ 。

经过以上分析，即可得到以下代码：

#include<iostream>
using namespace std;

long long x, y, a, b, ans = 0; // 开 long long

int main() {
    cin >> x >> y >> a >> b; // 输入
    while(x < y) {
        if(x < y / a && x * a < x + b) x *= a, ans ++; // 操作一比操作二更优，防止爆 long long 优化
        else break; // 操作二更优
    }
    ans += (y - x - 1) / b; // 计算操作二还可执行多少次
    cout << ans << endl; // 输出，换行好习惯
    return 0; 
}

提交记录

The End!!!!!

提交了 $5$ 次，我崩溃了 qwq。。

4|0AT_abc218_d 题解

洛谷链接&Atcoder

本篇题解为此题较简单做法及较少码量，并且码风优良，请放心阅读。

5|0题目简述

给定一个平面内的 $N$ 个点的坐标，求这 $N$ 个点中选 $4$ 个点可构成正方形的方案数。

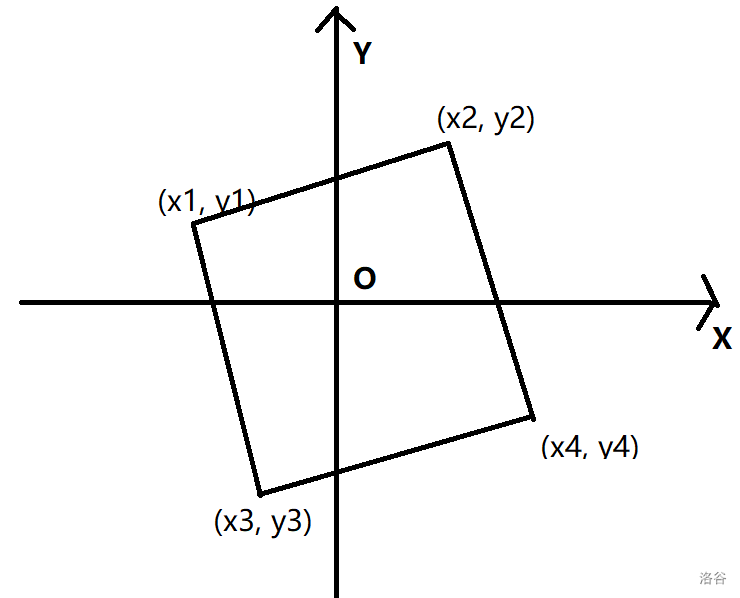
注：构成的正方形的边需平行于 $x$ 轴或 $y$ 轴。

例如下图就不符合要求，则不考虑这种情况：

6|0思路

此题基本纯思维题，算法考的不多。

一看数据范围， $4 \leq N \leq 2000$ ？既然数据范围这么小，那么 $O (N^{2})$ 的时间复杂度是能过的，但如果暴力枚举 $4$ 个点的话时间复杂度是 $O (N^{4})$ ，时间复杂度爆炸啊。

所以还是需要一点小优化的，本蒟蒻一开始只想到了枚举 $3$ 个点，接着判断另一个点是否存在，但这个想法的时间复杂度是 $O (N^{3})$ ，还是会超时。

那么我们沿袭这个思想就可以想到，直接 $N^{2}$ 枚举 $2$ 的点，接着判断另外两个点是否存在即可，但这枚举的两个点需为两个对角的点，这里我们枚举左上和右下两个点。

接着只需要解决如何判断另外两个点是否存在的问题即可，很容易想到用 map 容器去储存点是否存在的信息。

即可推出判断的语句： $m p_{x_{i}, y_{i}}$ 且 $m p_{x_{j}, y_{j}}$ 且 $m p_{x_{i}, y_{j}}$ 且 $m p_{x_{j}, y_{i}}$ 且 $x_{i} < x_{j}$ 且 $y_{i} < y_{j}$ 。

map 容器的初始化直接在输入时初始化即可。

经过以上分析，即可得出代码：

#include<iostream>
#include<map>
using namespace std;

int n, x[2005], y[2005];
long long ans = 0; // 开 long long 好习惯
map<int, map<int, bool> > mp; // 不要写成 >>，中间要有空格

int main() {
    cin >> n; // 输入
    for(int i = 1; i <= n; i ++) {
        cin >> x[i] >> y[i]; // 输入
        mp[x[i]][y[i]] = true; // 初始化处理
    }
    for(int i = 1; i <= n; i ++) {
        for(int j = 1; j <= n; j ++) {
            if(i == j) continue; // 特判 i = j 的情况
            if(mp[x[i]][y[i]] && mp[x[j]][y[j]] && mp[x[i]][y[j]] && mp[x[j]][y[i]] && x[i] < x[j] && y[i] < y[j]) ans ++; // 满足要求 ans++
        }
    }
    cout << ans << endl; // 输出，记得换行
    return 0;
}

提交记录

The End!!

7|0AT_abc215_d 题解

洛谷链接&Atcoder 链接

本篇题解为此题较简单做法及较少码量，并且码风优良，请放心阅读。

8|0题目简述

给定 $N$ ， $M$ 及含有 $N$ 个整数的序列 $A$ 。

求 $1 \sim M$ 中与所有 $a_{i}$ 均互质的整数及个数。

9|0思路

首先说一下最开始的想法。

直接暴力枚举 $1 \sim M$ 的数，再分别枚举每个数与 $a_{i}$ 是否互质，时间复杂度 $O (N \times M)$ 左右，一看数据范围直接爆炸，提交结果就可想而知了。

TLE $0$ 分代码如下，因为是暴力就不写注释了：

#include<iostream>
#include<cmath>
using namespace std;

int n, m, a[100005], num[100005], ans = 0;

int gcd(int x, int y) {
    return (y == 0 ? x : gcd(y, x % y));
}

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> a[i];
    for(int i = 1; i <= m; i ++) {
        bool flag = false;
        for(int j = 1; j <= n; j ++) 
            if(gcd(a[j], i) != 1) { flag = true; break; }
        if(!flag) ans ++, num[ans] = i;
    }
    cout << ans << endl;
    for(int i = 1; i <= ans; i ++) cout << num[i] << endl;
    return 0;
}

接下来让我们进行一点小优化。

既然对于 $1 \sim M$ 每个数进行暴力枚举会超时，那么就需要在输入时进行一些标记，经过一些尝试后发现，可以在输入时记录每个数的因数并标记在 $f l a g$ 数组中，看到 $a_{i}$ 的数据范围后发现可以用桶存。因为 $a_{i}$ 的因数会重复，所以在输入后需要另开一个 $v u l$ 存储序列 $A$ 的所有因数，不必用桶存。

如：

#define MAXN 1000000

void f(int x) {
    flag[x] = true;
    for(int i = 2; i * i <= x; i ++) 
        if(x % i == 0) flag[i] = flag[x / i] = true;
    return;
}
                             
int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) { cin >> x; f(x); }
    for(int i = 2; i <= MAXN; i ++) 
        if(flag[i]) vul[++ t] = i;
    return 0;
}

接着就可以不那么暴力的枚举了。

首先枚举 $1 \sim M$ 是一定的，但在第二层循环中仅需枚举当前 $i$ 是否为 $v u l$ 中因数的倍数，如果是直接跳出当前循环，如果跑了一遍 $v u l$ 发现当前 $i$ 不是任何 $v u l$ 中因数的倍数，则记录答案至数组 $n u m$ 中即可。

经过以上一点小优化，很容易即可写出代码：

#include<iostream>
#include<cmath>
using namespace std;

#define MAXN 1000000 // 最大值

int n, m, x, t, vul[MAXN + 5], num[MAXN + 5], ans, j;
bool flag[MAXN + 5];

void f(int x) {
    flag[x] = true;
    for(int i = 2; i * i <= x; i ++) // 遍历 x 求因数
        if(x % i == 0) flag[i] = flag[x / i] = true; // 标记 x 的因数
    return;
}

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) { cin >> x; f(x); } // 输入中处理
    for(int i = 2; i <= MAXN; i ++) 
        if(flag[i]) vul[++ t] = i;
    for(int i = 1; i <= m; i ++) {
        for(j = 1; j <= t; j ++)
            if(i % vul[j] == 0) break; // 不满足情况直接跳出循环
        if(j == t + 1) num[++ ans] = i; // 满足情况记录答案
    }
    cout << ans << endl; // 输出个数
    for(int i = 1; i <= ans; i ++) cout << num[i] << endl; // 输出答案
    return 0;
}

提交记录

The End!!!

10|0AT_abc246_d 题解

洛谷链接&Atcoder 链接

本篇题解为此题较简单做法及较少码量，并且码风优良，请放心阅读。

11|0题目简述

给定整数 $N$ ，请你找到最小的整数 $X$ ，满足：

$X \geq N$ 。
存在一对非负整数 $(a, b)$ ，使得 $X = a^{3} + a^{2} b + a b^{2} + b^{3}$ 。

12|0思路

首先可进行优化 $a^{3} + a^{2} b + a b^{2} + b^{3}$ 这一部分为 $(a^{2} + b^{2}) \times (a + b)$ 。

证明如下：

a^{3} + a^{2} b + a b^{2} + b^{3}

提取公因数 $a^{2}$ ：

= a^{2} \times (a + b) + a b^{2} + b^{3}

提取公因数 $b^{2}$ ：

= a^{2} \times (a + b) + b^{2} \times (a + b)

提取公因式 $a + b$ ：

= (a^{2} + b^{2}) \times (a + b)

接着因为 $a$ ， $b$ 并无实质性差异，故可以假设 $a \leq b$ 去用双指针确定 $X$ 的值。

可写一个 $check (x, y)$ 函数返回传入的 $x$ ， $y$ 的值，判断 $check (x, y)$ 是否 $\geq N$ ，如 $\geq N$ ，移动右区间并对答案取最小值，否则移动左区间即可。

注意： $a n s$ 初始化需初始化为一个较大值。

经过以上分析及小优化，很容易即可写出代码：

#include<iostream>
#include<cmath>
using namespace std;

long long n, x, l = 0, r = 1e6 + 1, ans = 0x3f3f3f3f3f3f3f3f; // ans 初始化为 long long 最大值

long long check(long long x, long long y) {
    return (long long)(pow(x, 2) + pow(y, 2)) * (x + y); // 小优化
}

int main() {
    cin >> n; // 输入
    // 双指针枚举
    while(l <= r) {
        if(check(l, r) < n) l ++; // 移动左区间
        else {
            ans = min(ans, check(l, r)); // 更新答案
            r --; // 移动右区间
        }
    }
    cout << ans << endl; // 输出答案，换行好习惯
    return 0;
}

提交记录

The end!!

13|0考试总结

可可口乐： 花费时间不多，这题应该是 $6$ 题中最简单的了， $d f s + 剪枝$ 即可。
卡牌： 题目不难，但在用 $m a p$ 实现时出现了一点小 $b u g$ ，用另一种方法解决了，但不幸 $T L E$ 了。赛后改了一下处理方式就 $A C$ 了。
上学： 细节比较多，但不难实现，这题是我写的最长但写的最快的一题。。
最大子数组： 此题在课上就~~没写对~~。在考场上能看懂题目，但实现出了问题。
大哈爱闯关： 考场写炸了，本来准备用贪心骗 $30$ 分，因为记得之前就是用贪心骗的分，但赛后一看我之前代码，居然是 $d f s$ 骗的分。。赛后看题解订正。
沙漠绿洲（加强版）： 时间分配不均，写到 $T 6$ 时间已经不够了，下次会注意。

The End

__EOF__

本文作者：So_noSlack
本文链接：https://www.cnblogs.com/So-noSlack/p/17576582.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！

posted @ 2023-07-24 19:29 So_noSlack 阅读(40) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· AT_abc180_d 题解

· 第十八节小组学习

· AtCoder Beginner Contest 300

· AtCoder Beginner Contest 361 补题记录（A~F）

· AtCoder Beginner Contest (ABC) 313 D-E

阅读排行：
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型，支持深度思考和联网搜索！
· 基于 Docker 搭建 FRP 内网穿透开源项目（很简单哒）
· ollama系列1：轻松3步本地部署deepseek，普通电脑可用
· 按钮权限的设计及实现
· 【杂谈】分布式事务——高大上的无用知识？

公告

第十三节小组学习

发表于 2023-07-24 19:29阅读：40评论：0推荐：0

集训

关注

跳至底部

昵称： So_noSlack
园龄： 1年9个月
粉丝： 14
关注： 0

+加关注

So_noSlack 的博客

第十三节小组学习

1|0AT_abc180_d 题解

2|0题目简述

3|0思路

4|0AT_abc218_d 题解

5|0题目简述

6|0思路

7|0AT_abc215_d 题解

8|0题目简述

9|0思路

10|0AT_abc246_d 题解

11|0题目简述

12|0思路

13|0考试总结

公告

So_noSlack

第十三节小组学习

搜索

常用链接

最新随笔

我的标签

积分与排名

合集 (6)

随笔档案 (112)

阅读排行榜

评论排行榜

推荐排行榜

最新评论

So_noSlack 的博客

第十三节 小组学习

1|0AT_abc180_d 题解

2|0题目简述

3|0思路

4|0AT_abc218_d 题解

5|0题目简述

6|0思路

7|0AT_abc215_d 题解

8|0题目简述

9|0思路

10|0AT_abc246_d 题解

11|0题目简述

12|0思路

13|0考试总结

公告

So_noSlack

第十三节 小组学习

搜索

常用链接

最新随笔

我的标签

积分与排名

合集 (6)

随笔档案 (112)

阅读排行榜

评论排行榜

推荐排行榜

最新评论

第十三节小组学习

第十三节小组学习