第十节 动态规划 - 2
初赛内容 : 数学
三角函数
定义
三角函数是数学中属于初等函数中的超越函数的函数。它们的本质是任何角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的。其定义域为整个实数域。另一种定义是在直角三角形中,但并不完全。现代数学把它们描述成无穷数列的极限和微分方程的解,将其定义扩展到复数系。
三角函数公式看似很多、很复杂,但只要掌握了三角函数的本质及内部规律,就会发现三角函数各个公式之间有强大的联系。而掌握三角函数的内部规律及本质也是学好三角函数的关键所在。
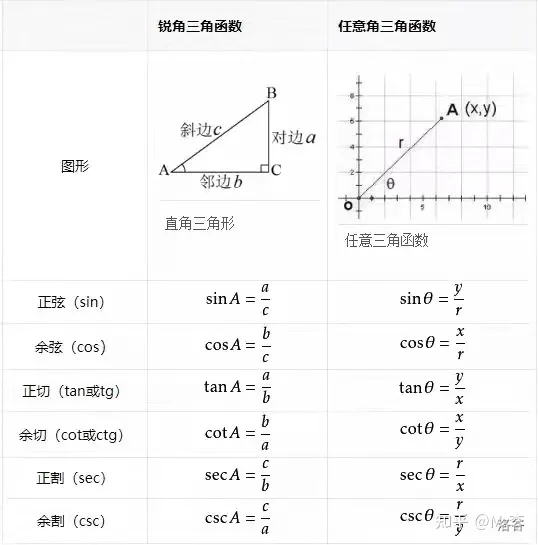
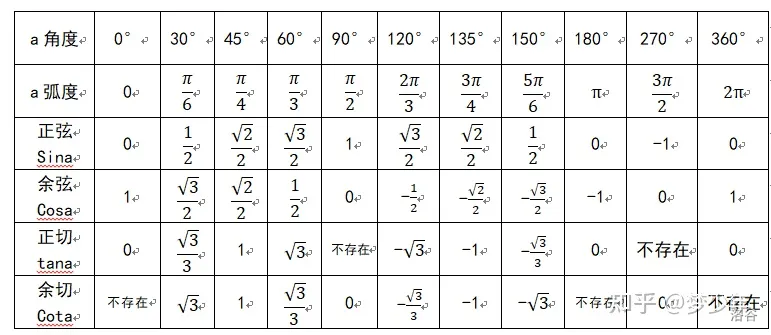
三角函数特殊值
对数函数
定义
对数函数(Logarithmic Function)是以幂(真数)为自变量,指数为因变量,底数为常量的函数。
对数函数是
如果
一般地,函数
其中
“log”是拉丁文logarithm(对数)的缩写,读作:[英][lɔɡ][美][lɔɡ, lɑɡ]。
对数函数特殊值
对数函数的特殊值 对数函数在数学学科中起着重要的作用,在各个领域均有广泛应用。 对数函数以对数底为底数,输入实数,通过公式
数学逻辑运算符
在形式逻辑中,逻辑运算符或逻辑联结词把语句连接成更复杂的复杂语句。例如,假设有两个逻辑命题,分别是“正在下雨”和“我在屋里”,我们可以将它们组成复杂命题“正在下雨,并且我在屋里”或“没有正在下雨”或“如果正在下雨,那么我在屋里”。一个将两个语句组成的新的语句或命题叫做复合语句或复合命题。
集合
概念
集合,简称集,是数学中一个基本概念,也是集合论的主要研究对象。集合论的基本理论创立于19世纪,关于集合的最简单的说法就是在朴素集合论(最原始的集合论)中的定义,即集合是“确定的一堆东西”,集合里的“东西”则称为元素。现代的集合一般被定义为:由一个或多个确定的元素所构成的整体 。
集合的类型
- 有限集和无限集
集合中元素的数目称为集合的基数,集合
- 空集
有一类特殊的集合,它不包含任何元素,如
-
空集
-
空集是任何一个集合的子集。
集合中元素的特性
- 确定性
给定一个集合,任给一个元素,该元素或者属于或者不属于该集合,二者必居其一,不允许有模棱两可的情况出现。
- 互异性
一个集合中,任何两个元素都认为是不相同的,即每个元素只能出现一次。有时需要对同一元素出现多次的情形进行刻画,可以使用多重集,其中的元素允许出现多次。
- 无序性
一个集合中,每个元素的地位都是相同的,元素之间是无序的。集合上可以定义序关系,定义了序关系后,元素之间就可以按照序关系排序。但就集合本身的特性而言,元素之间没有必然的序。
元素与集合的关系
- 属于
如果元素
- 不属于
如果元素
流程图
(略---)
同余定理
定义
数论中的重要概念。给定一个正整数
理论背景
数学上,两个整数除以同一个整数,若得相同余数,则二整数同余(英文:Modular arithmetic,德文:Kongruenz)。同余理论常被用于数论中。最先引用同余的概念与符号者为德国数学家高斯。同余理论是初等数论的重要组成部分,是研究整数问题的重要工具之一,利用同余来论证某些整除性的问题是很简便的。同余是数学竞赛的重要组成部分。
公元
同余符号
两个整数
记作:
读作:
定义
设
显然,有如下事实
(1)若
(2)
证明
充分性:
设
∵
则有
∵
∴
又∵
即
∴
性质
-
反身性:
-
对称性:若
-
传递性:若
-
同余式相加:若
-
同余式相乘:若
证明:
∵
∴
∴
故
- 线性运算:如果
(1)
(2)
证明:
(1)∵
∴
同理
∴
∴
∴
(2)∵
又
∴
∴
-
除法:若
特殊地 -
幂运算:如果
-
若
-
若
排列组合
概念
排列组合是组合学最基本的概念。所谓排列,就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。
排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。 排列组合与古典概率论关系密切。
发展历程
虽然数学始于结绳计数的远古时代,由于那时社会的生产水平的发展尚处于低级阶段,谈不上有什么技巧。随着人们对于数的了解和研究,在形成与数密切相关的数学分支的过
程中,如数论、代数、函数论以至泛函的形成与发展,逐步地从数的多样性发现数数的多样性,产生了各种数数的技巧。
同时,人们对数有了深入的了解和研究,在形成与形密切相关的各种数学分支的过程中,如几何学、拓扑学以至范畴论的形成与发展,逐步地从形的多样性也发现了数形的多样性,产生了各种数形的技巧。近代的集合论、数理逻辑等反映了潜在的数与形之间的结合。而现代的代数拓扑和代数几何等则将数与形密切地联系在一起了。这些,对于以数的技巧为中心课题的近代组合学的形成与发展都产生了而且还将会继续产生深刻的影响。
由此观之,组合学与其他数学分支有着必然的密切联系。它的一些研究内容与方法来自各个分支也应用于各个分支。当然,组合学与其他数学分支一样也有其独特的研究问题与方法,它源于人们对于客观世界中存在的数与形及其关系的发现和认识。例如,中国古代的《易经》中用十个天干和十二个地支以六十为周期来记载月和年,以及在洛书河图中关于幻方的记载,是人们至今所了解的最早发现的组合问题甚或是架构语境学。
于11和12世纪间,贾宪就发现了二项式系数,杨辉将它整理记载在他的《续古抉奇法》一书中。这就是中国通常称的杨辉三角。事实上,于12世纪印度的婆什迦罗第二也发现了这种组合数。13世纪波斯的哲学家曾讲授过此类三角。而在西方,布莱士·帕斯卡发现这个三角形是在17世纪中期。这个三角形在其他数学分支的应用也是屡见不鲜的。同时,帕斯卡和费马均发现了许多与概率论有关的经典组合学的结果。因此,西方人认为组合学开始于17世纪。组合学一词是德国数学家莱布尼茨在数学的意义下首次应用。也许,在那时他已经预感到了其将来的蓬勃发展。然而只有到了18世纪欧拉所处时代,组合学才可以说开始了作为一门科学的发展,因为那时,他解决了柯尼斯堡七桥问题,发现了多面体(首先是凸多面体,即平面图的情形)的顶点数、边数和面数之间的简单关系,被人们称为欧拉公式。甚至,当今人们所称的哈密顿圈的首创者也应该是欧拉。这些不但使欧拉成为组合学的一个重要组成部分——图论而且也成为占据现代数学舞台中心的拓扑学发展的先驱。同时,他对导致当今组合学中的另一个重要组成部分——组合设计中的拉丁方的研究所提出的猜想,人们称为欧拉猜想,直到1959年才得到完全的解决。
于19世纪初,高斯提出的组合系数,今称高斯系数,在经典组合学中也占有重要地位。同时,他还研究过平面上的闭曲线的相交问题,由此所提出的猜想称为高斯猜想,它直到20世纪才得到解决。这个问题不仅贡献于拓扑学,而且也贡献于组合学中图论的发展。同在19世纪,由乔治·布尔发现且被当今人们称为布尔代数的分支已经成为组合学中序理论的基石。当然,在这一时期,人们还研究其他许多组合问题,它们中的大多数是娱乐性的。
20世纪初期,庞加莱联系多面体问题发展了组合学的概念与方法,导致了近代拓扑学从组合拓扑学到代数拓扑学的发展。于20世纪的中、后期,组合学发展之迅速也许是人们
意想不到的。首先,于1920年费希尔(Fisher,R.A.)和耶茨(Yates,F.)发展了实验设计的统计理论,其结果导致后来的信息论,特别是编码理论的形成与发展.于1939年,坎托罗维奇(Канторович,Л.В.)发现了线性规划问题并提出解乘数法。于1947年丹齐克(Dantzig,G.B.)给出了一般的线性规划模型和理论,他所创立的单纯形方法奠定了这一理论的基础,阐明了其解集的组合结构。直到今天它仍然是应用得最广泛的数学方法之一。这些又导致以网络流为代表的运筹学中的一系列问题的形成与发展。开拓了人们称为组合最优化的一个组合学的新分支。在20世纪50年代,中国也发现并解决了一类称为运输问题的线性规划的图上作业法,它与一般的网络流理论确有异曲同工之妙。在此基础上又出现了国际上通称的中国邮递员问题。
另一方面,自1940年以来,生于英国的塔特(Tutte,W.T.)在解决拼方问题中取得了一系列有关图论的结果,这些不仅开辟了现今图论发展的许多新研究领域,而且对于20世纪30年代,惠特尼(Whitney,H.)提出的拟阵论以及人们称之为组合几何的发展都起到了核心的推动作用。应该特别提到的是在这一时期,随着电子技术和计算机科学的发展愈来愈显示出组合学的潜在力量。同时,也为组合学的发展提出了许多新的研究课题。例如,以大规模和超大规模集成电路设计为中心的计算机辅助设计提出了层出不穷的问题。其中一些问题的研究与发展正在形成一种新的几何,人们称之为组合计算几何。关于算法复杂性的究,自1971年库克(Cook,S.A.)提出NP完全性理论以来,已经将这一思想渗透到组合学的各个分支以至数学和计算机科学中的一些分支。
近20年来,用组合学中的方法已经解决了一些即使在整个数学领域也是具有挑战性的难题。例如,范·德·瓦尔登(Van der Waerden,B.L.)于1926年提出的关于双随机矩阵积和式猜想的证明;希伍德(Heawood,P.J.)于1890年提出的曲面地图着色猜想的解决;著名的四色定理的计算机验证和扭结问题的新组合不变量发现等。在数学中已经或正在形成着诸如组合拓扑、组合几何、组合数论、组合矩阵论、组合群论等与组合学密切相关的交叉学科。此外,组合学也正在渗透到其他自然科学以及社会科学的各个方面,例如,物理学、力学、化学、生物学、遗传学、心理学以及经济学、管理学甚至政治学等。
根据组合学研究与发展的现状,它可以分为如下五个分支:经典组合学、组合设计、组合序、图与超图和组合多面形与最优化.由于组合学所涉及的范围触及到几乎所有数学分支,也许和数学本身一样不大可能建立一种统一的理论.然而,如何在上述的五个分支的基础上建立一些统一的理论,或者从组合学中独立出来形成数学的一些新分支将是对21世纪数学家们提出的一个新的挑战。
在中国当代的数学家中,较早地在组合学中的不同方面作出过贡献的有 华罗庚、 吴文俊、 柯召、 万哲先、 张里千和 陆家羲等.其中,万哲先和他领导的研究组在有限几何方面的系统工作不仅对于组合设计而且对于图的对称性的研究都有影响.陆家羲的有关不交斯坦纳三元系大集的一系列的文章不仅解决了组合设计方面的一个难题,而且他所创立的方法对于其后的研究者也产生了和正产生着积极的作用。
1772年,法国数学家范德蒙德(Vandermonde, A. - T.)以[n]p表示由n个不同的元素中每次取p个的排列数。
瑞士数学家欧拉(Euler, L.)则于1771年以 及于1778年以 表示由n个不同元素中每次取出p个元素的组合数。
1830年,英国数学家皮科克(Peacock, G)引入符号Cr表示n个元素中每次取r个的组合数。
1869年或稍早些,剑桥的古德文以符号nPr 表示由n个元素中每次取r个元素的排列数,这用法亦延用至今。按此法,nPn便相当于n!。
1872年,德国数学家埃汀肖森(Ettingshausen,B. A. von)引入了符号(np)来表示同样的意义,这组合符号(Signs of Combinations)一直沿用至今。
1880年,鲍茨(Potts , R.)以nCr及nPr分别表示由n个元素取出r个的组合数与排列数。
1886年,惠特渥斯(Whit-worth, A. W.)用Cnr和Pnr表示同样的意义,他还用Rnr表示可重复的组合数。
1899年,英国数学家、物理学家克里斯托尔(Chrystal,G.)以nPr,nCr分别表示由n个不同元素中每次取出r个不重复之元素的排列数与组合数,并以nHr表示相同意义下之
可重复的排列数,这三种符号也通用至今。
1904年,德国数学家内托(Netto, E.)为一本百科辞典所写的辞条中,以Arn表示上述nPr之意,以Crn表示上述nCr之意,后者亦也用符号(n r)表示。这些符号也一直用到现代。
公式
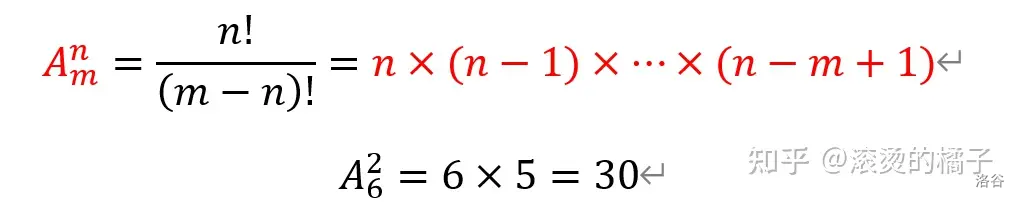

本文来自博客园,作者:So_noSlack,转载请注明原文链接:https://www.cnblogs.com/So-noSlack/p/17569390.html



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 使用C#创建一个MCP客户端
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· 按钮权限的设计及实现