第七节 搜索专题 - 3
A. 推箱子
题目描述:
推箱子是一个很经典的游戏.今天我们来玩一个简单版本.在一个 \(M \times N\) 的房间里有一个箱子和一个搬运工,搬运工的工作就是把箱子推到指定的位置,注意,搬运工只能推箱子而不能拉箱子,因此如果箱子被推到一个角上(如图 \(2\) )那么箱子就不能再被移动了,如果箱子被推到一面墙上,那么箱子只能沿着墙移动.
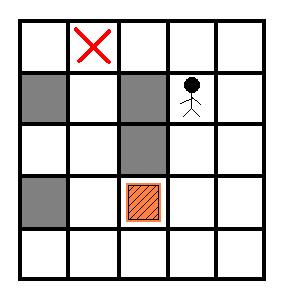
现在给定房间的结构,箱子的位置,搬运工的位置和箱子要被推去的位置,请你计算出搬运工至少要推动箱子多少格.
输入格式:
输入数据的第一行是一个整数 \(T\)(\(1 \le T \le 20\)),代表测试数据的数量.然后是 \(T\) 组测试数据,每组测试数据的第一行是两个正整数 \(M\),\(N\)(\(2 \le M,N \le 7\)),代表房间的大小,然后是一个 \(M\) 行 \(N\) 列的矩阵,代表房间的布局,其中 \(0\) 代表空的地板, \(1\) 代表墙, \(2\) 代表箱子的起始位置, \(3\) 代表箱子要被推去的位置,\(4\) 代表搬运工的起始位置.
输出格式:
对于每组测试数据,输出搬运工最少需要推动箱子多少格才能帮箱子推到指定位置,如果不能推到指定位置则输出 \(-1\).
样例输入:
1
5 5
0 3 0 0 0
1 0 1 4 0
0 0 1 0 0
1 0 2 0 0
0 0 0 0 0
样例输出:
4
数据规模:
见题面描述。
点击查看代码
int t;
int ax,ay,bx,by,cx,cy,n,m,step;
int f[10][10][10][10],a[10][10];
int dx[]={-1,0,1,0};
int dy[]={0,1,0,-1};
void dfs(int ax, int ay, int bx, int by, int cx, int cy,int step,int n,int m) {
if(f[ax][ay][bx][by] <= step) return;
f[ax][ay][bx][by] = step;
if (ax == cx && ay == cy) return;
for (int i = 0; i < 4; i++) {
int nx = bx + dx[i], ny = by + dy[i];
if(!(nx >= 1 && nx <= n && ny >= 1 && ny <= m && a[nx][ny] != 1)) continue;
if(nx == ax && ny == ay){
int tx = ax+dx[i],ty = ay+dy[i];
if(!(tx >= 1 && tx <= n && ty >= 1 && ty <= m && a[tx][ty] != 1)) continue;
dfs(tx,ty,nx,ny,cx,cy,step+1,n,m);
}
else {
dfs(ax,ay,nx,ny,cx,cy,step,n,m);
}
}
}
int main() {
scanf("%d", &t);
while (t--) {
scanf("%d %d", &n, &m);
memset(f,0x3f,sizeof(f));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
scanf("%d", &a[i][j]);
if (a[i][j] == 2)ax = i, ay = j;//箱子
if (a[i][j] == 4)bx = i, by = j;//人
if (a[i][j] == 3)cx = i, cy = j;//目标位置
}
}
dfs(ax, ay, bx, by, cx, cy, 0, n, m);
int ans = f[0][0][0][0];
for(int i=0;i<4;i++){
int nx = cx+dx[i],ny=cy+dy[i];
if(1<=nx&&nx<=n&&1<=ny&&ny<=m&&a[nx][ny]!=1)
ans = min(ans,f[cx][cy][nx][ny]);
}
if(ans == f[0][0][0][0])cout<<"-1\n";
else cout<<ans<<endl;
}
return 0;
}
编译结果
compiled successfully
time: 2ms, memory: 392kb, score: 100, status: Accepted
> test 1: time: 0ms, memory: 392kb, points: 10, status: Accepted
> test 2: time: 0ms, memory: 392kb, points: 10, status: Accepted
> test 3: time: 0ms, memory: 392kb, points: 10, status: Accepted
> test 4: time: 0ms, memory: 392kb, points: 10, status: Accepted
> test 5: time: 0ms, memory: 392kb, points: 10, status: Accepted
> test 6: time: 0ms, memory: 392kb, points: 10, status: Accepted
> test 7: time: 1ms, memory: 392kb, points: 10, status: Accepted
> test 8: time: 0ms, memory: 392kb, points: 10, status: Accepted
> test 9: time: 1ms, memory: 392kb, points: 10, status: Accepted
> test 10: time: 0ms, memory: 392kb, points: 10, status: Accepted
B. 迷宫难题
题目描述:
这是一个 \(n\) 行 \(m\) 列的迷宫,某些格子有若干枚钥匙。相邻格子之间有一扇门,门上有若干把锁,所有的锁都打开才能够通行,若没有锁则直接通行。对应的钥匙可以打开对应的锁,钥匙和锁的类型范围由数字 \(0\) 到 \(p\) 表示。每一步可以走到周围四连通的格子之一,门可以从两个方向打开,捡钥匙和开锁不消耗时间。问从 (\(1, 1\)) 到 (\(n, m\)) 最少需要走多少步。
输入格式:
第一行三个整数 \(n,m,p\)。
第二行一个整数 \(K\),
接下来 \(K\) 行每行 \(5\) 个整数 \(x_1, y_1, x_2, y_2, t\),表示 (\(x_1, y_1\)) 与 (\(x_2, y_2\)) 之间的门上有一把 \(t\) 类型的锁。
保证 (\(x_1, y_1\)) 与 (\(x_2, y_2\)) 相邻。
下一行一个整数 \(S\),表示钥匙的个数。
接下来 \(S\) 行每行三个整数 \(x, y, t\),表示 \(x,y\) 处有一枚 \(t\) 类型的钥匙。
输出格式:
输出一行表示答案。
样例输入:
4 4 9
9
1 2 1 3 2
1 2 2 2 0
2 1 2 2 0
2 1 3 1 0
2 3 3 3 0
2 4 3 4 1
3 2 3 3 0
3 3 4 3 0
4 3 4 4 0
2
2 1 2
4 2 1
样例输出:
14
数据规模:
\(N,M,P \le 10\), \(K < 150\), \(S \le 150\)。
点击查看代码
#define MAXN 12
queue<pair<pair<int, int>, int> > q;
int n, m, p, k, x1, x2, y3, y2, t, s, x, y, cur, ans;
bool vis[MAXN][MAXN][2050];
int gate[MAXN][MAXN][MAXN][MAXN], key[MAXN][MAXN], dis[MAXN][MAXN][2050];
int dx[] = { -1,0,1,0 };
int dy[] = { 0,1,0,-1 };
int main() {
pair<pair<int, int>, int> cur;
scanf("%d %d %d", &n, &m, &p);
scanf("%d", &k);
for (int i = 1; i <= k; i++) {
scanf("%d %d %d %d %d", &x1, &y3, &x2, &y2, &t);
gate[x1][y3][x2][y2] |= (1 << t);
gate[x2][y2][x1][y3] |= (1 << t);
}
scanf("%d", &s);
for (int i = 1; i <= s; i++) {
scanf("%d %d %d", &x, &y, &t);
key[x][y] |= (1 << t);
}
memset(dis, 0x3f, sizeof(dis));
dis[1][1][key[1][1]] = 0;
vis[1][1][key[1][1]] = true;
q.push(make_pair(make_pair(1, 1), key[1][1]));
while (!q.empty()) {
cur = q.front(); q.pop();
x = cur.first.first;
y = cur.first.second;
k = cur.second;
for (int i = 0; i < 4; i++) {
int nx = x + dx[i], ny = y + dy[i];
if (nx >= 1 && nx <= n && ny >= 1 && ny <= m && (k & gate[x][y][nx][ny]) == gate[x][y][nx][ny]) {
int nk = k | key[nx][ny];
if (!vis[nx][ny][nk]) {
vis[nx][ny][nk] = true;
dis[nx][ny][nk] = dis[x][y][k]+1;
q.push(make_pair(make_pair(nx, ny), nk));
}
}
}
}
ans = dis[0][0][0];
for (int i = 0; i < (1 << 11); i++) ans = min(ans, dis[n][m][i]);
if (ans == dis[0][0][0]) cout << "-1\n";
else cout << ans << endl;
return 0;
}
编译结果
compiled successfully
time: 7ms, memory: 1876kb, score: 100, status: Accepted
> test 1: time: 0ms, memory: 1876kb, points: 10, status: Accepted
> test 2: time: 0ms, memory: 1876kb, points: 10, status: Accepted
> test 3: time: 1ms, memory: 1876kb, points: 10, status: Accepted
> test 4: time: 1ms, memory: 1876kb, points: 10, status: Accepted
> test 5: time: 1ms, memory: 1876kb, points: 10, status: Accepted
> test 6: time: 1ms, memory: 1876kb, points: 10, status: Accepted
> test 7: time: 0ms, memory: 1876kb, points: 10, status: Accepted
> test 8: time: 2ms, memory: 1876kb, points: 10, status: Accepted
> test 9: time: 1ms, memory: 1876kb, points: 10, status: Accepted
> test 10: time: 0ms, memory: 1876kb, points: 10, status: Accepted
C. 大学生活
题目描述:
大学的课程是在不同教室上的,需要同学们在不同时间自己去上课。
小Q 当前位置在 \(A\),他下一门课在 \(B\) 处上,他想知道最短多少次操作才能到达 \(B\)。
一次操作可以是:朝当前方向走一步、向左转、向右转、向后转。
初始时小Q可以任选一个朝向。
输入格式:
第一行包含一个整数 \(n\),表示大学的边长。
接下来 \(n\) 行,每行一个长度为 \(n\) 的字符串。'x' 表示障碍物,'.' 表示道路。
输出格式:
输出一个整数表示答案,走不到则输出 \(-1\)。
样例输入:
3
.xA
...
Bx.
样例输出:
6
数据规模:
\(2 \le N \le 100\)。
点击查看代码
#define MAXN 105
int n, ans = -1;
int xy[4][2] = { {1, 0}, {0, 1}, {-1, 0}, {0, -1} };
char mp[MAXN][MAXN];
bool vis[MAXN][MAXN][4];
struct node{ int x, y, step, p; };
void bfs(int x,int y){
queue<node> q;
q.push({x, y, 0, -1});
while(q.size()) {
node t = q.front();
if(mp[t.x][t.y] == 'B') {
ans = t.step;
return;
}
q.pop();
for(int i = 0; i < 4; i ++) {
int xx = t.x + xy[i][0], yy = t.y + xy[i][1];
if(xx >= 1 && xx <= n && yy >= 1 && yy <= n && mp[xx][yy] != 'x' && vis[xx][yy][i] == 0) {
if(t.p == -1 || t.p == i) {
vis[xx][yy][i] = 1;
q.push({xx, yy, t.step + 1, i});
}
else
q.push({t.x, t.y, t.step + 1, i});
}
}
}
}
int main(){
cin >> n;
int x, y;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++) {
cin >> mp[i][j];
if(mp[i][j] == 'A') x = i, y = j;
}
bfs(x, y);
cout << ans << endl;
return 0;
}
编译结果
compiled successfully
time: 12ms, memory: 3600kb, score: 100, status: Accepted
> test 1: time: 0ms, memory: 3492kb, points: 10, status: Accepted
> test 2: time: 2ms, memory: 3544kb, points: 10, status: Accepted
> test 3: time: 2ms, memory: 3428kb, points: 10, status: Accepted
> test 4: time: 1ms, memory: 3420kb, points: 10, status: Accepted
> test 5: time: 1ms, memory: 3432kb, points: 10, status: Accepted
> test 6: time: 2ms, memory: 3444kb, points: 10, status: Accepted
> test 7: time: 1ms, memory: 3600kb, points: 10, status: Accepted
> test 8: time: 2ms, memory: 3440kb, points: 10, status: Accepted
> test 9: time: 0ms, memory: 3436kb, points: 10, status: Accepted
> test 10: time: 1ms, memory: 3360kb, points: 10, status: Accepted
初赛知识 : 算法
介绍
什么是算法?
有一个很著名的公式 “程序 = 数据结构 + 算法”。
曾经跟朋友吃饭的时候我问他什么是算法,他说算法嘛,就是一套方法,需要的时候拿过来,套用就可以,我吐槽他,他说的是小学数学题的算法,不是编程的算法。
从字面意义上解释,就是用于计算的方法,通过该这种方法可以达到预期的计算结果。目前,被广泛认可的算法专业定义是:算法是模型分析的一组可行的,确定的,有穷的规则。通俗的说,算法也可以理解为一个解题步骤,有一些基本运算和规定的顺序构成。但是从计算机程序设计的角度看,算法由一系列求解问题的指令构成,能根据规范的输入,在有限的时间内获得有效的输出结果。算法代表了用系统的方法来描述解决问题的一种策略机制。
完成同一件事的不同的算法完成的时间和占用的资源可能并不相同,这就牵扯到效率的问题。算法的基本任务是针对一个具体的问题,找到一个高效的处理方法,从而完成任务。而这就是我们的责任了。
特征
一个典型的算法一般都可以抽象出 \(5\) 个特征:
有穷性:算法的指令或者步骤的执行次数和时间都是有限的。
确切性:算法的指令或步骤都有明确的定义。
输入:有相应的输入条件来刻画运算对象的初始情况。
输出:一个算应有明确的结果输出。
可行性:算法的执行步骤必须是可行的。
分类
- 根据应用分:
按照算法的应用领域,可以分为基本算法,数据结构相关算法,几何算法,图论算法,规划算法,数值分析算法,加密解密算法,排序算法,查找算法,并行算法,数值算法……
- 根据确定性分:
-
确定性算法:有限时间内完成,得到结果唯一。
-
非确定性算法:有限时间内完成,得到结果不唯一,存在多值性。
- 根据算法的思路分:
递推算法,递归算法,穷举算法,贪婪算法,分治算法,动态规划算法,迭代算法等。
算法和公式的关系
算法 >= 公式
如果没有接触到编程,的确很容易将算法理解为数学公式。公式的确具备算法的特征,但是算法并不等于公式,公式是一种高度精简的算法,算法的形式可以比公式更复杂,解决的问题更加广泛。
算法和程序的关系 程序也是算法的一种表现形式,也是一种工具
算法和数据结构的关系
数据结构是数据的组织形式,可以用来表现特定的对象数据。
因为不同的数据结构所采用的处理方法不同,计算的复杂程度也不同,因此算法往往依赖于某种某种数据结构。数据结构是算法实现的基础。
复杂度
时间复杂度和空间复杂度是衡量一个算法效率的重要标准。
- 基本操作数
同一个算法在不同的计算机上运行的速度会有一定的差别,并且实际运行速度难以在理论上进行计算,实际去测量又比较麻烦,所以我们通常考虑的不是算法运行的实际用时,而是算法运行所需要进行的基本操作的数量。
在普通的计算机上,加减乘除、访问变量(基本数据类型的变量,下同)、给变量赋值等都可以看作基本操作。
对基本操作的计数或是估测可以作为评判算法用时的指标。
- 时间复杂度
定义
衡量一个算法的快慢,一定要考虑数据规模的大小。所谓数据规模,一般指输入的数字个数、输入中给出的图的点数与边数等等。一般来说,数据规模越大,算法的用时就越长。而在算法竞赛中,我们衡量一个算法的效率时,最重要的不是看它在某个数据规模下的用时,而是看它的用时随数据规模而增长的趋势,即 时间复杂度。
引入
考虑用时随数据规模变化的趋势的主要原因有以下几点:
-
现代计算机每秒可以处理数亿乃至更多次基本运算,因此我们处理的数据规模通常很大。如果算法 \(A\) 在规模为 \(n\) 的数据上用时为 \(100n\) 而算法 \(B\) 在规模为 \(n\) 的数据上用时为 \(n^2\),在数据规模小于 \(100\) 时算法 \(B\) 用时更短,但在一秒钟内算法 \(A\) 可以处理数百万规模的数据,而算法 \(B\) 只能处理数万规模的数据。在允许算法执行时间更久时,时间复杂度对可处理数据规模的影响就会更加明显,远大于同一数据规模下用时的影响。
-
我们采用基本操作数来表示算法的用时,而不同的基本操作实际用时是不同的,例如加减法的用时远小于除法的用时。计算时间复杂度而忽略不同基本操作之间的区别以及一次基本操作与十次基本操作之间的区别,可以消除基本操作间用时不同的影响。
当然,算法的运行用时并非完全由输入规模决定,而是也与输入的内容相关。所以,时间复杂度又分为几种,例如:
-
最坏时间复杂度,即每个输入规模下用时最长的输入对应的时间复杂度。在算法竞赛中,由于输入可以在给定的数据范围内任意给定,我们为保证算法能够通过某个数据范围内的任何数据,一般考虑最坏时间复杂度。
-
平均(期望)时间复杂度,即每个输入规模下所有可能输入对应用时的平均值的复杂度(随机输入下期望用时的复杂度)。
所谓「用时随数据规模而增长的趋势」是一个模糊的概念,我们需要借助下文所介绍的 渐进符号 来形式化地表示时间复杂度。
本文来自博客园,作者:So_noSlack,转载请注明原文链接:https://www.cnblogs.com/So-noSlack/p/17559109.html

