直接选择排序（选择排序）-八大排序汇总（1）

工作原理：

　　每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

稳定性：

　　选择排序是不稳定的排序方法（比如序列[5， 5， 3]第一次就将第一个[5]与[3]交换，导致第一个5挪动到第二个5后面）。

时间复杂度：

　　比较次数O(n^2），比较次数与关键字的初始状态无关，总的比较次数N=(n-1）+(n-2）+...+1=n*(n-1）/2。

　　交换次数O(n），最好情况是，已经有序，交换0次；最坏情况下，即待排序记录初始状态是按第一条记录最大，之后的记录从小到大顺序排列，则需要移动记录的次数最多为3（n-1），逆序交换n/2次。

空间复杂度：

　　O(1)。简单选择排序需要占用一个临时空间，在交换数值时使用。

比较：

　　与插入排序比较：直接选择排序和直接插入排序类似，都将数据分为有序区和无序区，所不同的是直接播放排序是将无序区的第一个元素直接插入到有序区以形成一个更大的有序区，而直接选择排序是从无序区选一个最小的元素直接放到有序区的最后。选择排序是固定位置，找元素。相比于插入排序的固定元素找位置，是两种思维方式。

　　与冒泡排序比较：冒泡算法最费时的一是两两比较，二是两两交换，选择排序中交换次数比冒泡排序少多了，n值较小时，选择排序比冒泡排序快。

示例

 

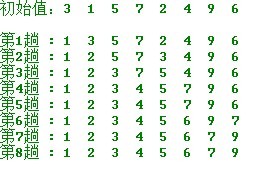
代码：

void Selectsort(int a[], int n)
{
    int i, j, nMinIndex;
    for (i = 0; i < n; i++)
    {
        nMinIndex = i; //找最小元素的位置
        for (j = i + 1; j < n; j++)
            if (a[j] < a[nMinIndex])
                nMinIndex = j;

        Swap(a[i], a[nMinIndex]); //将这个元素放到无序区的开头
    }
}

inline void Swap(int &a, int &b)
{
    int c = a;
    a = b;
    b = c;
}

注意swap交换，若如下不用中间变量，会有一个隐患，如果a, b指向的是同一个数，那么调用Swap1()函数会使这个数为0

inline void Swap1(int &a, int &b)
{
    a ^= b;
    b ^= a;
    a ^= b;
}

这种情况下可以在Swap1()中加个判断，如果二个数据相等就不用交换了

inline void Swap1(int &a, int &b)
{
    if (a != b)
    {
        a ^= b;
        b ^= a;
        a ^= b;
    }
}