算法——排序——交换排序(2)——快速排序
什么是快速排序（QuickSort）
快速排序（Quicksort）是对冒泡排序的一种改进。基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
快速排序是对冒泡排序的升级版。
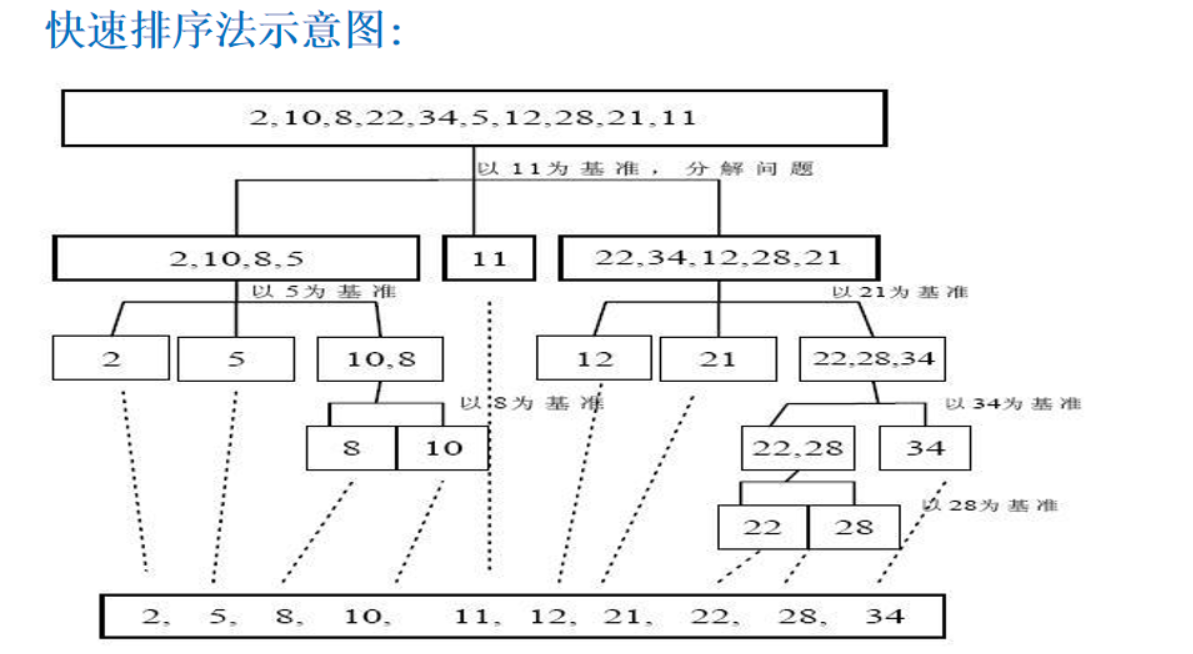
去数组中的某个数做为基准值将数组分为两部分，其中一部分的所有数都比另一部分大，再对这两部分也进行取基准分组，最后直到每个分组都只剩下一个数。
代码实现快速排序
其实快速排序很简单，只需要写出来一个交换，就可以利用这个交换一直递归就好了。
核心算法都在交换的这个函数里面，该函数主要实现的代码逻辑就是：随便选一个在范围内的数作为基准，然后对该所有的数跟该基准进行比较来选择是在左边还是右边。
这里的例子程序是：实现从小到大的排序，每次的基准选取范围的最左边的数作为基准将其用一个temp临时值存起来，然后右指针先开始从右往左移动进行比较，如果有比基准小的就放到该基准数的数组的位置（因为基准值是已经被存起来了的），然后这个时候被移动的数的位置可以被别的填充了，就再从左往右来移动，如果比基准大就放那个之前的位置，因为已经可以被填充了，就这样一直递归，知道左边的指针和右边的指针相等，然后最初的基准值就存储到相等的位置就好了。
如果还不理解，推荐看看这个视频：https://www.bilibili.com/video/BV1UK41137q7?p=17&spm_id_from=pageDriver
void QuickSort(int* a, int Left,int Right)
{
//一个快排的接口
quickSort(a,Left,Right);
for (int i = 0; i <= Right; i++)
{
cout << a[i] << " ";
}
cout << endl;
}
void quickSort(int* a, int Left, int Right)
{
//递归的思想来递归进行快排
if (Left < Right)//如果Left等于Right说明这个分组只有一个数据就不用排了,得两个和两个以上才有意义
{
int mid = partition(a, Left, Right);//该函数在对分组进行选基准然后分组后，会返回一个基准的下标
quickSort(a, Left, mid - 1);
quickSort(a, mid + 1, Right);
}
}
int partition(int *a,int Left,int Right)
{
//该函数用来对某一个分组进行选取基准并将该分组剩下的数判断是在左边还是右边
//这里采用将分组的第一个数作为基准
int temp = a[Left];
while(Left < Right)//如果left==right说明
{
while (a[Right] > temp && Left < Right)//从右边往左找，直到找到小于的，或者达到了一样大
{
Right--;
}
a[Left] = a[Right];
while (a[Left] < temp && Left < Right)//从左往右找，直到找到比基准大的，或者达到了一样大就退出。
{
Left++;
}
a[Right] = a[Left];
}
a[Left] = temp;
return Left;
}
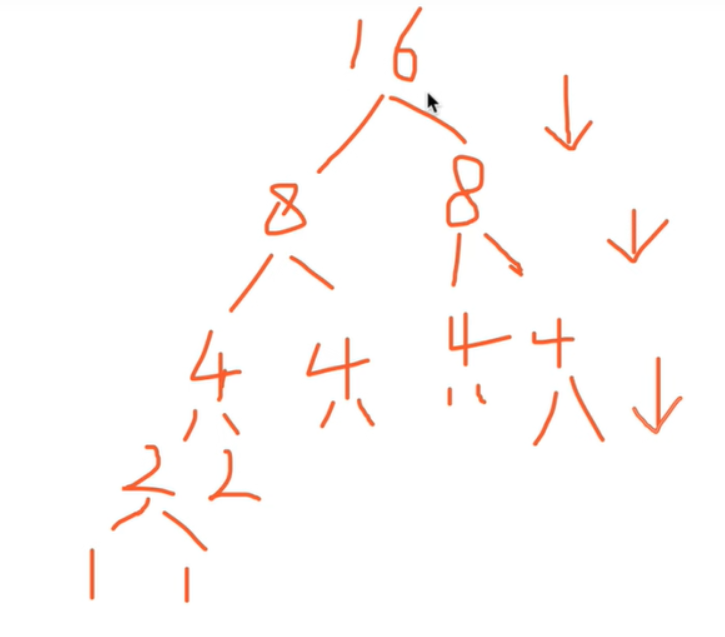
快速排序的时间复杂度
假设数组有16个数，而且每次分都是平均分，那么对于每个组里面调用的partition该函数，该函数的时间复杂度是n，而调用的次数又是对数来计算，所以得出快速排序的时间复杂度是O(nlogn)，这是最好的情况。最坏的情况就是已经排好了顺序，这个时候就只有一边需要排序，就只对左边进行partition，或只对右边进行partition。也就是说 1234567,或者7654321这种已经有顺序的就是最差情况，平均情况的算法效率O(nlogn)
