图如何利用代码来实现
邻接矩阵
图的邻接矩阵存储方式是用两个数组来表示图。
一个一维数组存储图中顶点信息,
一个二维数组(邻接矩阵)存储图中的边或弧的信息。
设图G有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:
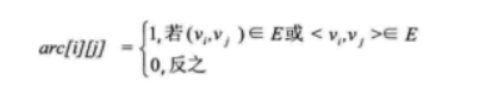
看一个实例,下图左就是一个无向图
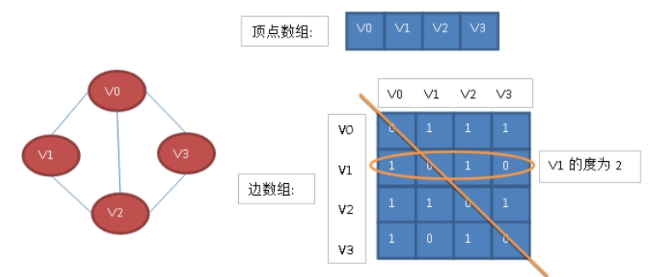
从上面可以看出,无向图的边数组是一个对称矩阵。所谓对称矩阵就是n阶矩阵的元满足aij = aji。即从矩阵的左上角到右下角的主对角线为轴,右上角的元和左下角相对应的元全都是相等的。
从这个矩阵中,很容易知道图中的信息。
(1)判断任意两顶点是否有边无边;
(2)某个顶点的度,其实就是这个顶点vi在邻接矩阵中第i行或(第i列)的元素之和
(3)求顶点vi的所有邻接点就是将矩阵中第i行元素扫描一遍,arc【i】【j】为1就是邻接点
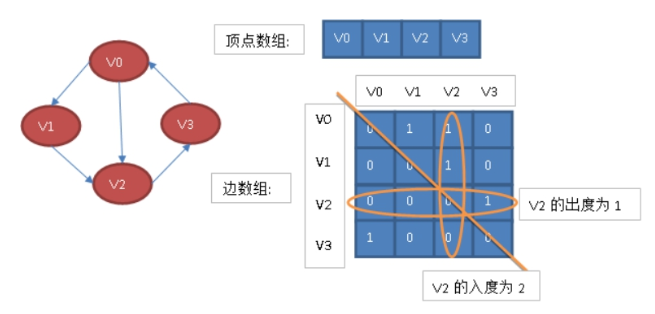
而有向图讲究入度和出度,顶点v2的入度为2,正好是第i列各数之和。顶点v2的出度为1,即第i行的各数之和。
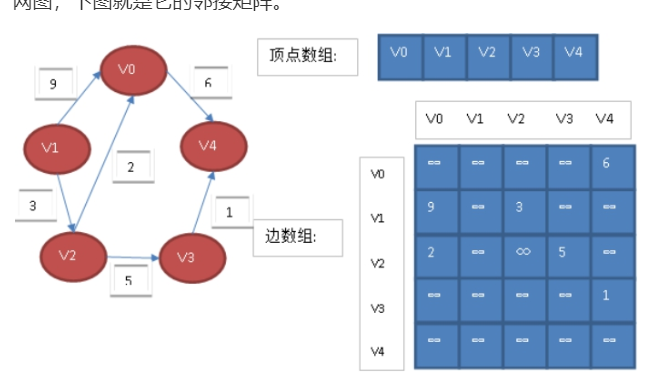
若图G是网图,有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:

这里的wij表示(vi,vj)上的权值。无穷大表示一个计算机允许的、大于所有边上权值的值,也就是一个不可能的极限值。下面左图就是一个有向网图,下图就是它的邻接矩阵。
无向图代码实现:https://www.cnblogs.com/Sna1lGo/p/14348948.html
有向图代码实现:https://www.cnblogs.com/Sna1lGo/p/14348966.html
邻接表
邻接矩阵是不错的一种图存储结构,但是,对于边数相对顶点较少的图,这种结构存在对存储空间的极大浪费。因此,找到一种数组与链表相结合的存储方法称为邻接表。
邻接表的存储方式是这样的:
(1) 图中顶点用一个一维数组存储,当然,顶点也可以用单链表来存储,
不过,数组可以较容易的读取顶点的信息,更加方便。
(2) 图中每个顶点vi的所有邻接点构成一个线性表,由于邻接点的个数不定,所以,用单链表存储,无向图称为顶点vi的边表,有向图则称为顶点vi作为弧尾的出边表。
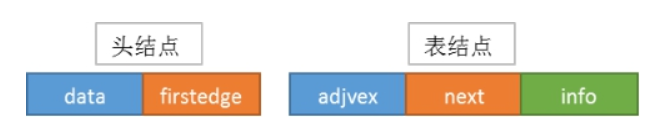
数据结构定义:
例如,下图就是一个无向图的邻接表的结构。
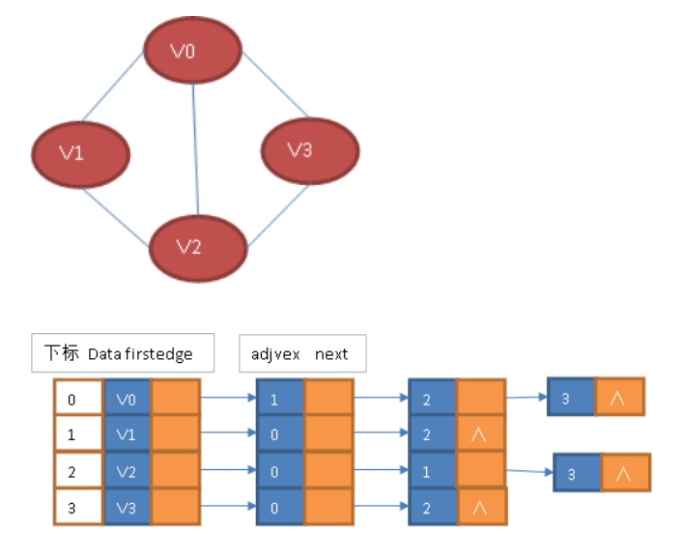
从图中可以看出,顶点表的各个结点由data和firstedge两个域表示,data是数据域,存储顶点的信息,firstedge是指针域,指向边表的第一个结点,即此顶点的第一个邻接点。边表结点由adjvex和next两个域组成。adjvex是邻接点域,存储某顶点的邻接点在顶点表中的下标,next则存储指向边表中下一个结点的指针。
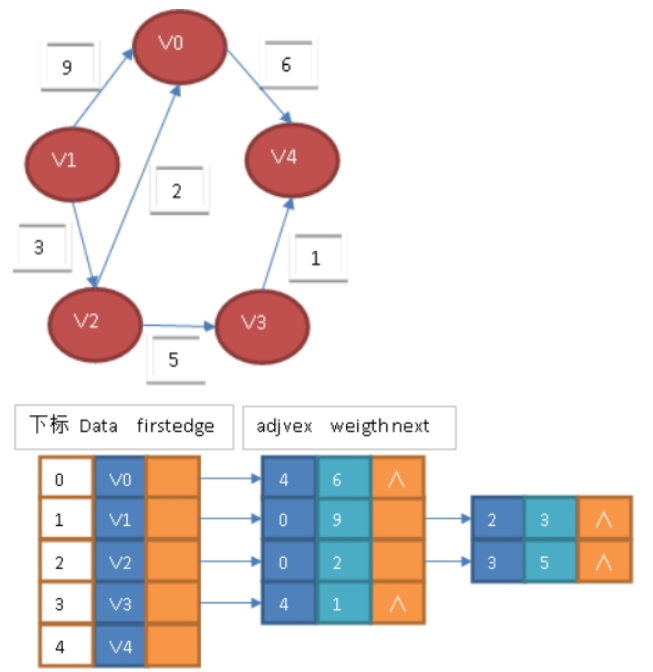
对于带权值的网图,可以在边表结点定义中再增加一个weight的数据域,存储权值信息即可。如下图所示。
邻接表有向图的代码实现:https://www.cnblogs.com/Sna1lGo/p/14366667.html



