图的概念
图的定义和术语
图的定义
图是由顶点的有穷非空集合和顶点之间的边的集合组成的,通常表示为G=(V,E),其中,G表示一个图,V表示G中顶点的集合,E表示G中边的集合
无向边
若顶点Vi 到Vj 的边没有方向,则称这条边为无向边,用无序偶对
(Vi ,Vj)来表示
有向边
若从顶点Vi 到Vj的边有方向,则称这条边为有向边,也称为弧(Arc)。用有序偶对<Vi ,Vj>来表示。Vi称为弧尾(Tail)或初始点,Vj称为弧头(Head)或终端点。
(v1,v2)和(v2,v1)是两个不同的有向边
无向图
如果图中任意两个顶点之间的边都是无向边,则称该图为无向图。
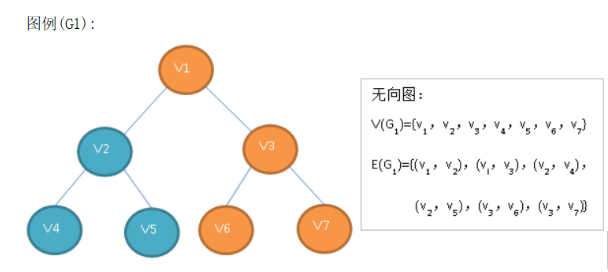
有向图
如果图中任意顶点之间的边都是有向边,则称该图为有向图

无向完全图
在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。含有n个顶点的无向完全图有n(n-1)/2条边。
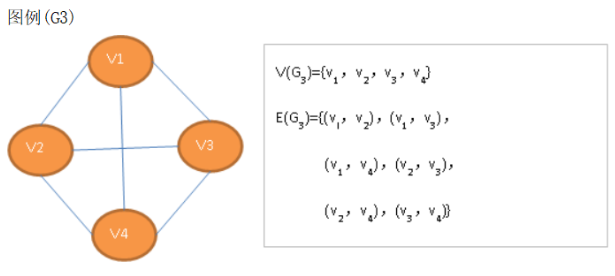
有向完全图
在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。含有n个顶点的有向完全图有n(n-1)条边。
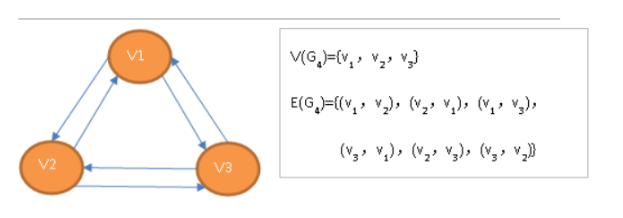
图的顶点数n和边数e的关系
1 如果是无向图
0<=e<=n*(n-1)/2
刚好为n*(n-1)/2为无向完全图
2 如果是有向图
0<=e<=n*(n-1)
刚好为n*(n-1)就是完全有向图
连通图
在无向图G=(V,E)中,如果从顶点v到顶点w有路径,则称v和w是相通的。如果对图中任意两个顶点Vi和Vj 属于E,则两个顶点是连通的,则称G是连通图。
连通图生成树
连通图的生成树是一个极小的连通子图,它含有图中全部的n个顶点,但只有足以构成一棵树的n-1条边。
术语
稀疏图: 有很少条边或弧的图。
稠密图: 有很多条边或弧的图。
权: 有时图的边或弧具有与它相关的数,这种与图的边或弧相关的数叫做权。
网:带权的图通常称为网。
度:顶点的度是指和该顶点关联的边的数目。
入度:有向图中以顶点(v)为头的弧的数目,称为(v)的入度。
出度:有向图中以顶点(v)为尾的弧的数目,称为(v)的出度。
邻接点:对于无向图,同一边上的两个顶点称为邻接点。
子图: 假设两个图G=(V,E)和G1=(V1,E1),如果V1⊆V且E1⊆E则G1为G的子图
路径的长度: 路径上的边或弧的数目。




