CryptoHack做题记录

一、GENERAL

1.ENCODING

ASCII

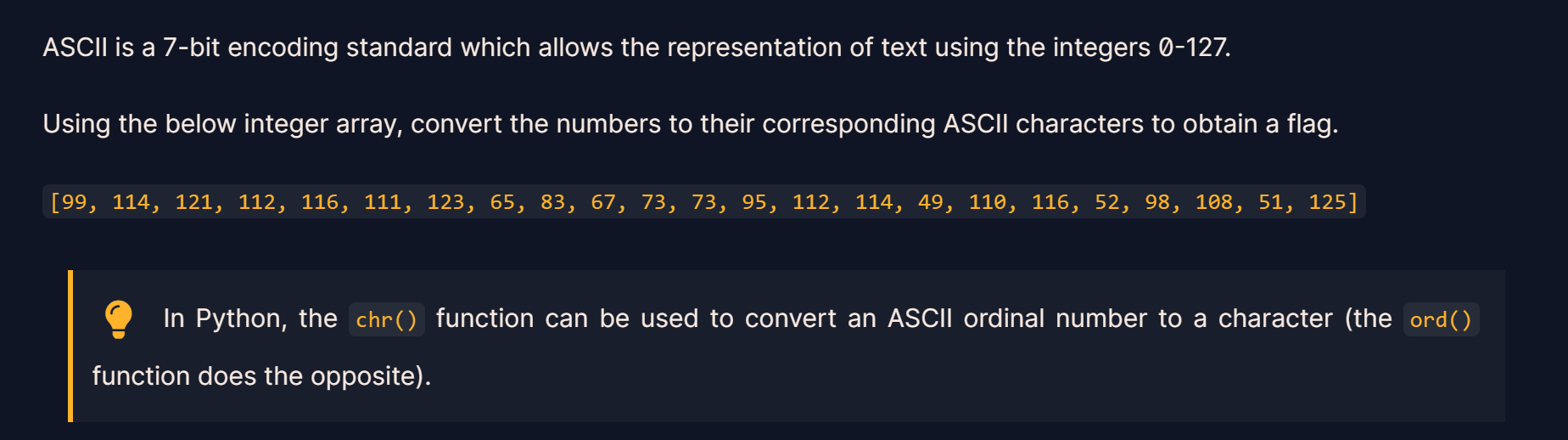
ascii = [99, 114, 121, 112, 116, 111, 123, 65, 83, 67, 73, 73, 95, 112, 114, 49, 110, 116, 52, 98, 108, 51, 125]
for char in ascii:
    print(chr(char),end='')

crypto{ASCII_pr1nt4bl3}

Hex

Hex='63727970746f7b596f755f77696c6c5f62655f776f726b696e675f776974685f6865785f737472696e67735f615f6c6f747d'
print(bytes.fromhex(Hex))

crypto{You_will_be_working_with_hex_strings_a_lot}

Bytes and Big Integers

from Crypto.Util.number import *
Long = 11515195063862318899931685488813747395775516287289682636499965282714637259206269
print(long_to_bytes(Long))

crypto{3nc0d1n6_4ll_7h3_w4y_d0wn}

2.XOR

XOR Starter

String='label'
for i in String:
    print(chr(ord(i)^13),end='')

crypto{aloha}

XOR Properties

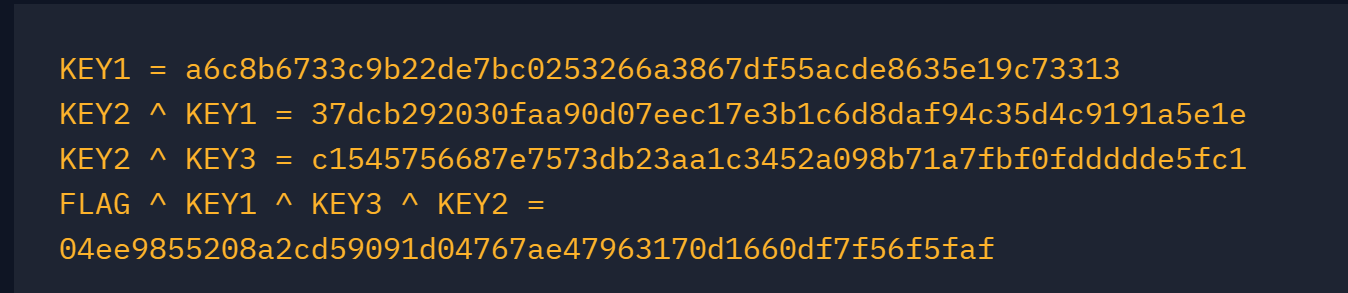
from Crypto.Util.number import *
KEY1 = 0xa6c8b6733c9b22de7bc0253266a3867df55acde8635e19c73313
KEY2_KEY1 = 0x37dcb292030faa90d07eec17e3b1c6d8daf94c35d4c9191a5e1e
KEY2_KEY3 = 0xc1545756687e7573db23aa1c3452a098b71a7fbf0fddddde5fc1
FLAG_KEY1_KEY3_KEY2 = 0x4ee9855208a2cd59091d04767ae47963170d1660df7f56f5faf
print(long_to_bytes(FLAG_KEY1_KEY3_KEY2^KEY2_KEY3^KEY1))

crypto{x0r_i5_ass0c1at1v3}

Favourite byte

from Crypto.Util.number import *
a=0x73626960647f6b206821204f21254f7d694f7624662065622127234f726927756d
print(long_to_bytes(a))
A=b"sbi`d\x7fk h! O!%O}iOv$f eb!'#Ori'um"
B=b'crypto{'
for i,j in zip(A,B):
    print(i^j)
for i in A:
    print(chr(i^16),end='')

• 思路：已知flag头：crypto{根据此可找到异或的字节

crypto{0x10_15_my_f4v0ur173_by7e}

You either know, XOR you don't

• 思路：我们已知flag头为crypto{}

  我们可以根据这个恢复key

from Crypto.Util.number import *
from pwn import *

a = 0x0e0b213f26041e480b26217f27342e175d0e070a3c5b103e2526217f27342e175d0e077e263451150104
A = b"\x0e\x0b!?&\x04\x1eH\x0b&!\x7f'4.\x17]\x0e\x07\n<[\x10>%&!\x7f'4.\x17]\x0e\x07~&4Q\x15\x01\x04"
B = b'crypto{'
print(xor(long_to_bytes(a), B))
print(xor(b'\x04', b'}'))

恢复出key为：myXORkey

然后解密：

print(xor(long_to_bytes(a),b'myXORkey'))

crypto{1f_y0u_Kn0w_En0uGH_y0u_Kn0w_1t_4ll}

Lemur XOR

两张图片的RGB分别xor：

from PIL import Image

image1 = Image.open(r"D:\download\flag_7ae18c704272532658c10b5faad06d74.png")
pic1 = image1.load()
image2 = Image.open(r"D:\download\lemur_ed66878c338e662d3473f0d98eedbd0d.png")
pic2 = image2.load()
width, height = image1.size
for i in range(width):
    for j in range(height):
        r1, g1, b1 = pic1[i, j]
        r2, g2, b2 = pic2[i, j]
        pic1[i, j] = (r1 ^ r2, g1 ^ g2, b1 ^ b2)
image1.show()

3.MATHMATICS

Greatest Common Divisor

求gcd(66528,52920)，没什么好说的

Extended GCD

拓展欧几里得：

Modular Arithmetic 1

求余数，略

Modular Arithmetic 2

欧拉定理：

若a和m互质，即\((a,m)\equiv 1\)，有\(a^{\varphi(m)}\equiv 1(modm)\)

题目让Calculate 27324678765465536 mod 65537
显然为1

Modular Inverting

求3 * d ≡ 1 mod 13，也就是求3对模13的模逆

print(gmpy2.invert(3,13))

二、MATHEMATICS

1.MODULAR MATH

Quadratic Residues

p = 29
ints = [14, 6, 11]

让我们找出ints列表里模p的二次剩余，需要用到欧拉判别法：

写一个脚本判断一下即可：

ints = [14, 6, 11]
p = 29
for t in ints:
    for i in range(1, p):
        if pow(i, 2, p) == t:
            print(f"{i} ^ 2 = {t} mod 29")

Legendre Symbol

p =
ints = []

我们要求满足\(x^2\equiv ints(modp)\)的x的值

我们需要找到，ints中的这些数，哪些满足\((\frac{a}{p})=1\)

可以写个脚本：

p = 
ints = []
num = 0
for a in ints:
    if pow(a, p // 2, p) == 1:
        print(a)

发现85256449776780591202928235662805033201684571648990042997557084658000067050672130152734911919581661523957075992761662315262685030115255938352540032297113615687815976039390537716707854569980516690246592112936796917504034711418465442893323439490171095447109457355598873230115172636184525449905022174536414781771满足条件

然后根据\((\frac{a}{p})=a^{\frac{p-1}{2}}(modp)\equiv1\)

变形：\(a^{\frac{p+1}{2}}(modp)\equiv a\)

即：$(a^{\frac{p+1} {4}})^{2}\equiv a(modp) $

而正好p是模4余3的，则\(a^{\frac{p+1}{4}}(modp)\)就是我们要找的根

print(pow(a,p//4+1,p))

即为flag

Modular Square Root

使用Tonelli-Shanks算法计算二次剩余

可以用python的sympy模块实现

给出a和p的值，计算\(a^2=x(modp)\)中x的值

from sympy.ntheory.residue_ntheory import nthroot_mod
a = 
p = 
x = nthroot_mod(a,2,p)
print(x)

Chinese Remainder Theorem

中国剩余定理（CRT）

x ≡ 2 mod 5
x ≡ 3 mod 11
x ≡ 5 mod 17

直接使用sagemath