单变量线性回归

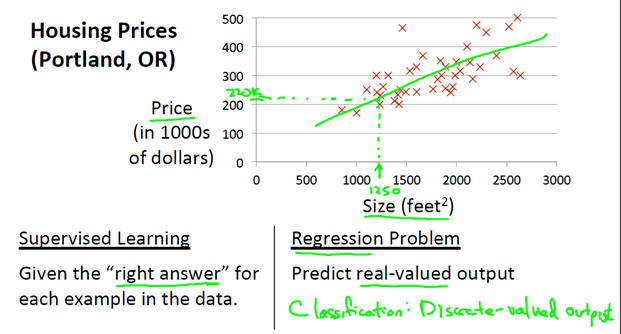
这是一个单变量（房子的面积）问题。这是一个监督学习的问题，对于每一个数据我们都给出了一个正确的price。

准备工作：

在书中他的表示是 hθ(x) = θ0 + θ1x1，它的意思是因为只有一个变量x1所以称之为单变量线性回归。

这些都目前看来没有什么问题。下一步提出了一个代价函数的感念，也就是说。每一次预测出的误差都是应该被思考的。

jθ被称为代价函数， [hθ(x) = θ0 + θ1x1] - real(price)=mistakes = jθ

为了防止出现正负变换，所以用 (θ0 + θ1x - y)的平方这样的方式，这也就是说式子进一步简化之后可以得出一个这样的式子:

θ0和θ1对于代价函数的影响是一个U字形的。

下一步简单的让它自己改变一下θ0和θ1

这里书本中引入的概念是梯度下降，公式如下：

上面的公式是一个位置更新公式，一个赋值等号，对θi进行不断的更新，α是学习速率。第一次更新的时候，默认θi是X的话，α*1*X，那么西塔i第一次更新之后就是αX，然后对i进行替换，0123456789....，当jθ慢慢变小的时候，θi的△也越来越小，反之。

这就是代价函数，但其实不一定要用那个偏导的参数，因为如果是一次的话其实是不会改变的，所以其实可以用别的代替

如果我自己定义代价函数的话:针对一次二次三次次数，可以用不用的值直接代替，或者用一个很小的固定值虽然会增加循环的次数，但是就不会看起来这么搞了。