SVM 支持向量机

1. 支持向量

1.1 线性可分

首先我们先来了解下什么是线性可分。

在二维空间上，两类点被一条直线完全分开叫做线性可分。

简单说就是如图上这样，一个线（FX）把D1和D0分为两个类，FD1>0,FD2<0

1.2 最大间隔超平面

当进入一个三维的时候，这个分割就变成了一个木板，具体做的就是把这个分割尽可能的看起来合理一些（不偏向任何一边，做到公平合适）

为了使这个超平面更具鲁棒性，我们会去找最佳超平面，以最大间隔把两类样本分开的超平面，也称之为最大间隔超平面。

• 两类样本分别分割在该超平面的两侧；
• 两侧距离超平面最近的样本点到超平面的距离被最大化了。

1.3 支持向量

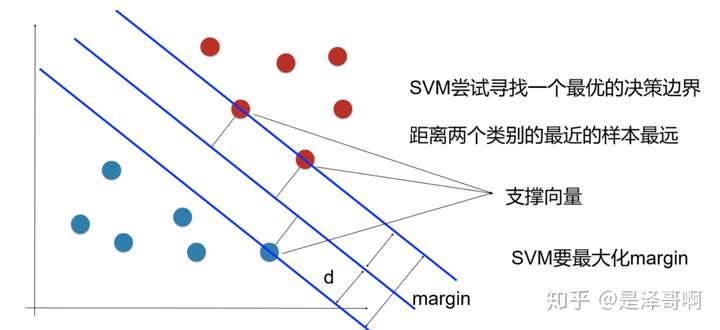样本中距离超平面最近的一些点，这些点叫做支持向量。

1.4 SVM 最优化问题

SVM 想要的就是找到各类样本点到超平面的距离最远，也就是找到最大间隔超平面。任意超平面可以用下面这个线性方程来描述：

二维空间点 （x,y)到直线 AX+BY+C=0的距离公式是：

扩展到 n 维空间后 ，点X（X1,X2...）到直线的距离是：

其中W=直线参数的平方和的根

如图所示，根据支持向量的定义我们知道，支持向量到超平面的距离为 d，其他点到超平面的距离大于 d。

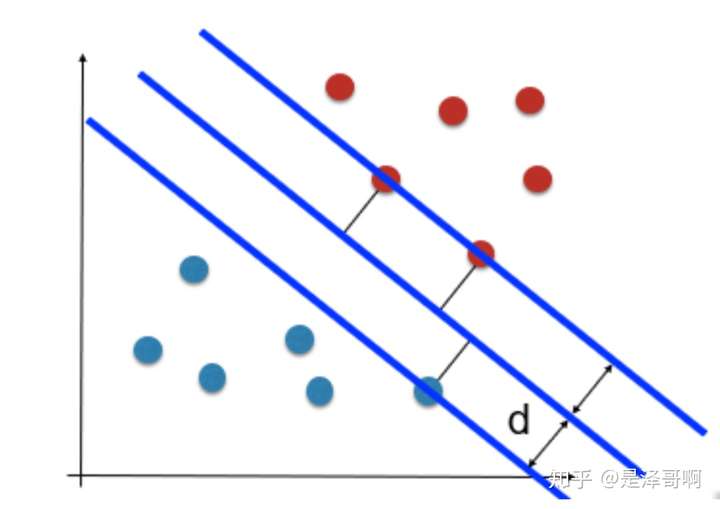
于是我们有这样的一个公式：

每个支持向量到超平面的距离可以写为：

所以得到的最优化问题是：