偏差-方差权衡

偏差度量了学习算法的期望预测与真实结果的偏离程度，刻画了学习算法本身的拟合能力。

方差度量了同样大小的训练集的变动所导致的学习性能的变化，刻画了数据扰动所造成的影响。

噪声表达了当前任务上任何学习算法所能达到的期望泛化误差的下界，也就是最小值。

泛化误差可以分解为偏差、方差和噪声之和。

一般来说，偏差和方差是有冲突的，成为偏差-方差窘境（Bias- Variance dilemma）

1） 训练程度不足时，学习器的拟合能力不够强，训练数据的扰动不足以使学习器产生显著变化，偏差将主导泛化错误率。

2）训练程度加深，学习器的拟合能力逐渐增强，训练数据发生的扰动逐渐能够被学习器学到，方差将主导泛化错误率。

3）训练程度充足后，学习器的拟合能力已经非常强，训练数据发生的轻微扰动都会导致学习器发生显著变化。训练数据非全局的特征如果被学习器学到了，将发生过拟合。

吴恩达的《深度学习》课程中提到理解偏差和方差的两个关键数据：

Train set error（训练集误差） 和 Dev set error （开发集误差）

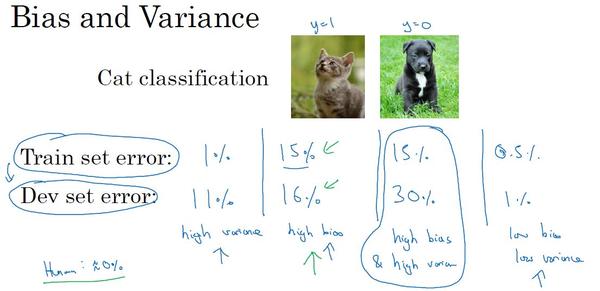
可以看到，若我们假设贝叶斯误差为0，也就是人类的错误率接近于0%。

1）若训练集误差很接近人类的可避免误差，并且和开发集误差相差很大时，我们称此情况为高方差。模型过度拟合了训练数据。

2）若训练集误差与贝叶斯误差相差较大，同时接近开发集误差时，称之为高偏差。算法没有在数据集上得到很好的训练，对训练数据欠拟合。

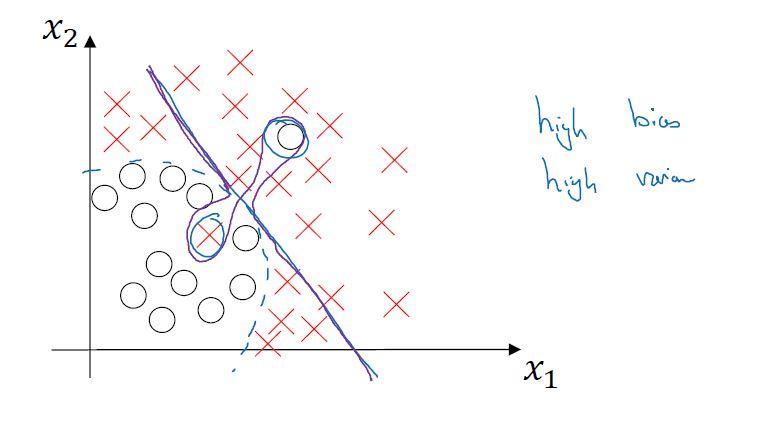
3）若训练集误差与贝叶斯误差相差较大，同时与开发集误差也相差较大时，此时为高偏差高方差情形。参见下图，这是一个整体为线性，但在局部具有高灵活性，能够过度拟合部分数据的线性分类器。

4）若训练集误差非常接近贝叶斯误差，同时开发集误差也非常接近训练集误差，那么就是我们期望的低偏差低方差状态。

下面看另外一个问题，为什么在深度学习中不用太关注偏差-方差权衡？

这需要了解一下在偏差-方差权衡问题解决中的办法。

对于高偏差问题，我们一般采用：

a. 更加复杂的模型

b. 增加训练时间

对于高方差问题，则采取：

a. 更多的训练数据

b. 正则化

因此，在目前的大数据时代和深度学习算法不断进步的今天，只要我们训练一个更大的神经网络，准备了更多的训练数据，就解决了以上问题。可以做到仅仅减小方差或偏差，而不对另一方产生过多影响。也就是方差和偏差的相关性减弱了。