聚类基本数学模型

　　聚类方法是一类用途非常广泛的算法，聚类包含很多各式各样的算法。所有这些算法都有它的基本数学模型。本文就简单介绍一下聚类的基本数学模型。了解了基本数学模型就了解了聚类最本质的原理。无论是学习算法还是自己开发新的算法，学习基本数学模型都是很有帮助的。本文的目的一方面是介绍数学模型，另一方面也算是自己学习内容的一个记录吧。

　　假设X＝{x₁,x₂,…,x_n}是待分析的对象全体，也可称为论域或样本集合。X中的每个对象（也可称为样本）常用有限个参数值来刻画（这里的参数值也可称为样本的属性值），每个参数值用于刻画x_i的某个特征（属性）。于是对象x_i就伴随着一个向量P(x_i)=(x_i1,x_i2,…,x_im), 其中x_ij()是x_i在j个特征上的值，P(x_i)称为x_i的特征向量或模式向量（也可理解为用于定义聚类中心的向量，不过这样的理解并不严谨，因为并非每种聚类方法都是以类似于KMEANS那样的中心点来定义簇的，所以在数据模型中以P(x_i)来表示在意义上更加抽象）。聚类分析就是分析论域或样本集合X中的n个样本所对应的模式矢量间的空间距离及分散情况，按照各样本间的距离远近或相似程度把x₁, x₂,…, x_n划分成k个不相交的模式子集X₁, X₂, …, X_k，并要求满足下列条件：

样本对子集的隶属度关系可用隶属度函数表示为：

 

 

其中，隶属度函数必须满足条件。也就是说：

1. 要求每一个样本能且只能隶属于某一类。
2. 要求每个子类都是非空的。

   

　　在这个表达式中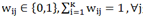是用于约束"每一个样本能且只能属于某一类"；用于约束"每个子类都是非空的"。将以上定义的隶属度函数w_ij扩展到[0,1]这个区间即为模糊聚类的定义。模糊聚类又称为软聚类，相应的非模糊聚类也可称为硬聚类。