Docker:从容<器>到集装箱设计之<道>
By 高焕堂 (台灣Docker論壇 主席)
misoo.tw@qq.com 2015/03/13
高焕堂的相关文章:
A01、从「集装箱」思考Docker风潮:Docker潮流下的赢家策略
B01、Android和Docker的一致架构设计(1):追求今天决策的未来性
B02、Android和Docker的一致架构设计(2):包装<跨集装箱>的通信协议
B03、Android和Docker的一致架构设计(3):建立企业主的<核心集装箱>
B04、Android和Docker的一致架构设计(4):<分合自如>的设计模式
前言
道家名師 徐文兵說到:
「从道家传承来讲,它强调四个字,叫“道、法、术、器”。
- “道”是天道,“法”是人定的,就是说你该怎么跟着“天道”去做。
- “法”也有善恶之分。顺应天道的“法”就是善法,相反,违背天道的“法”就是恶法。
- “术”是指技术层面上的操作方法。
- “器”是指有型的物质或是有形的工具。」
许多事物都可以从这四个层面(Dimension)去看。换句话说,我们都可以从四个不同的视角(View)去看一件事物。无论是<层面>或<视角>,意味了它们都不是事物的本体(Reality),而只是人们内心对该事物本体的认知(Perception)而已。所以,这些视角本身都没有对错之分,唯有坚持单一视角才可能是错的。

图-1、多个视角看Docker集装箱
同样的,今天大家迎接云平台的集装箱技术风潮,我们也都能从上述的四个视角来看待“Docker Container”。例如,从器的视角来看它,就可以称它为<Docker容器>;此外,从道、法或术的视角来看它,也可特别称它为<Docker集装箱>。于是,在本文里我将从<道>的视角来谈谈我心中对“Docker Container”事物的认知,与大家分享我内心所看到的景象(但只是Image而非Reality)。
1、集装箱之<道>
《老子第25章》中书:「人法地,地法天,天法道,道法自然。」所谓道法自然,就是效法或遵循自然之意。因此,我们就来观察自然界生物的设计,大多面对一项限制,就是:信息的有限性(Information Limitations)。
信息的有限性
关于<信息的有限性>与自然造物法则,在生物学界的探讨已经非常多了。由于这项限制,一个生物形体的造成,是出自一个概括性的计划:单纯而<一致的造形>。随着生物的成长、与环境的交互信息越多,逐渐在细节上修修补补,就发展出<不同的内涵>。然后,基于单纯的造形,不断进行<重复的组合>。例如,漂亮的枫叶林,就是合乎“单纯造形、不同内涵、重复组合”三项特性。许多造形相同(且不同细节)的枫叶,组合出一遍美丽的树林,如下图:

图-2、造物法则之美
再如人们的手掌的造形也都极为相似,其细节纹路也各不相同,也满足上述三项特性。在最具爆发力的工业设计品中,你常常可以发现其杰作具有其特色:一致造形、包容变化、无限组合。其中最典型的是:船运业的集装箱(Container)。它兼具了这三项自然特质,因而带来了无比巨大的商业潜力和商机。所以我们常说,“一致造形、包容变化、无限组合”三项特性是集装箱的本质(Essence)或设计之道。如果您查阅牛津字典,会发现“Essential”这个字是“不可或缺”的意思。也就是说,“一致造形、包容变化、无限组合”三者是集装箱所不可或缺的特质。
集装箱的身影
无论是实际物品、抽象概念或梦想思维,只要兼具这三项特质的东西,就呈现出集装箱的身影了。凡是在革命性的转折里,就经常会出现集装箱的身影。例如,在软件开发方面,人们也受限于<信息的有限性>,必须透过优越的架构设计,来提供给后续维运人员依据布署环境的现实条件而进行修修补补,因而出现Docker集装箱身影,并蔚为风潮。Docker集装箱让人们避免过度设计(Over-Designed),不去冻结未来(Frozen Future),遵循集装箱之<道>,创造整体圆满。
2、一致造形与减法设计
一致造形
刚才提到了集装箱的自然特质:“一致造形、包容变化、无限组合”。

图-3、集装箱的本质
因为单纯一致造形(简称“单一造形”或“一致造形”)又具有极大的包容力和弹性,所以能组合出无限花样。任何事物或系统的组织和外貌往往各不相同,例如各种花朵或化合物(如玻璃、陶瓷)的结构和外貌都不一样,但其幕后有一致的造形,就是:原子(Atom)造形。基于造形的一致不变,而其内涵和组合可变,能创造不同结构,并呈现出了多样化的外貌。
序中有乱
因此,一致的造形,让人们创造了气象万千的架构,以及与众不同的产品。从“一致造形,内涵可变”而观之,集装箱创造了「序中有乱」。集装箱的外表简单有序,所有能迭得很高,呈现巨大而且井然有序;集装箱的内部是空的,用来容纳多样化而繁杂的物品;这种情形称为序中有乱(变化)。由于序中有乱的威力,让一种很简单的东西,发挥了巨大的力量,改变了整个运输产业,也改变了人们的生活。

图-4、<序中有乱>设计思维
此外,从“一致造形,无限组合”而观之,集装箱创造了「乱中有序」。无论是「乱中有序」或「序中有乱」,两者都要呈现出序(Order),并包容变化(Change),只是手段不同而已。例如,前面提过的枫叶是个造形,经由简单重复组合及修修补补而成为一棵树,甚至一个森林,看来是乱中有序。当我们反向细观叶子内部的复杂,也会看到叶子也是一个整体,也是由更小的单位、更简单而一致的造形(序)而形成的,看到的是序中有乱。
减法设计
无论自然界或文艺界,在乱中有序的外貌下,常常蕴藏常了序中有乱的设计。包括艺术家、设计师都在规划序中有乱。例如,诗人的无限自由创意是“加法设计”,而幕后常用一致的造形来表达其“减法设计”。就如同唐诗的七言绝句,它的一致造形(4个句字,每句7字,4种韵律),让李白、杜甫、白居易人人都能发挥创意、尽情思考,但都以一致的造形来表述(Represent)。不但没有伤害创意,而且还基于<书同文、诗同形>而相互激发创作的氛围。

图-5、唐诗<一致的造形>
此外,科学家们也在自然界的复杂(乱中有序)外貌下,以序中有乱的视角去寻觅幕后蕴藏的一致造形,包括原子、分子、细胞等。这些一致造形处处表达了自然界的减法设计。

图-6、力求减法设计
虽然一致造形的轮廓相同,组成元素种类也相同,然而其内部元素,以及元素的不同组合,赋予各个造形不同的内涵。在物理学上的原子造形也是如此,氢原子(H)和氧原子(O)两者的都是原子造形。这两个造形轮廓相同(都是原子造形),但是内涵不同。基于固定而有限的元素种类(如质子、中子、电子三种元素),加上简单的组合规律(如电子围绕质子和中子),形成了单纯而<一致的造形>。一致造形的减法设计发挥出<序中有乱>的特质,带来一样的巨大潜能,蔚为风潮。
加法设计
一致造形除了能包容复杂之外,还让人们容易重複组合出大系统。例如,樱花就是一个造形,规范了花瓣、花蕊、花衬叶等有限小元素的组合规律,表达了减法设计。同时它无限重复组合(即加法设计)成为整个美不胜收的漂亮樱花山谷。同样的,氢原子(H)和氧原子(O)两者的都有一致的原子造形,既规范内部有限的元素组合规律,也规范原子之间的组合规律。例如,两个氢原子和一个氧原子能组合成为水分子,而水分子则无限(重复)组合成为一杯水,或巨大的海洋。因此,我们说<一致造形、包容变化>是从复杂到简单的减法设计;而<一致造形、无限组合>则是从简单到复杂的加法设计。

图-7、支撑加法设计
一致造形(如Docker集装箱,或原子结构),它们把变化封装起来,凸显简单秩序,人们拥有确定感,并通过秩序来掌握变化,人们比较不会害怕变化。因为秩序简单而令人着迷,因为变化无穷而令人惊叹它的无限潜能。这就是集装箱、原子和DNA等一致造形的减法设计具有革命性威力的来源:和谐而充满能量。因此,人们通常必须仰赖有效的减法设计(如集装箱等一致造形),才敢大胆去作加法,创造无限的新奇组合。
图-8、力求有效减法,才能大幅开放加法
无论是人造的或自然界的事物,在其生命周期中,都将面对非常复杂的环境变化。因此设计师或造物者都以开放的心境、力求加法、调整自己去适应环境变化。然而,在设计期间(Design-time),设计师(或造物者)受限于<信息的有限性>,无法预知未来的变化,又要避免过度设计而冻结未来。于是,遵循自然之道:力求有效的减法,才能大胆开放加法。以此观之,Docker集装箱的有效减法设计,将带给人们高度和谐而充满能量,并蔚为革命性风潮。
3. Docker的小集装箱设计:EIT造形
Docker集装箱与EIT造形
Docker集装箱是个单纯的<一致造形>,以序中有乱的视角,将复杂多变包装起来,呈现出简单易用的序。这个序呈现出来,就是集装箱的接口了。此外,在Docker集装箱的潮流下,将涌现更多的小集装箱新造形和接口,也将涌现较大的集装箱新造形和接口。所以,一致造形在设计上有两层作用:
- 规范集装箱内部的小元素组合规律,让人们容易打包集装箱的内容。例如,Docker规范了Docker镜像的标准格式(Format)。
- 规范集装箱之间的组合规律;让人们容易无限组合出大系统。例如,从Docker Hub或Registry中取得Docker镜像来做多样化组合。
在上述两个层面,Docker都能表现得很好了。然而,在运行期间,如何将集装箱里的微服务(Micro-Service)组合出多样化的应用(App)呢? 由于这涉及企业的业务逻辑(Business Logic)的变化,也让Docker设计者(如同自然造物者)也面临<信息的有限性>的限制:无法准确预测未来,又要避免过度设计而冻结未来(Frozen Future)。因此,我们需要再设计一个单纯的造形来提供给后续企业运营环境的现实条件变化而进行修修补补。于是,我(高焕堂)提出了单纯而一致的造形,我称之为:EIT造形。它就成为Docker集装箱里的App层小集装箱。
从汽车设计理解EIT造形
首先,请您观察一下,汽车设计者(如同自然造物者)如何面对<信息的有限性>的挑战:无法准确预测未来,又要避免冻结未来。

图-9、汽车设计者面对<信息的有限性>
从EIT 造形与原子造形的对比,很容易理解到造形内部元素之间,有其组合与互动的韵律(或规律)。基于固定而有限的元素种类(如质子、中子、电子三种元素),加上简单的组合规律(如电子围绕质子和中子),形成所谓的单纯「一致的造形」。同样地,EIT造形也是基于固定而有限的元素种类(如引擎、接口、轮胎三种元素),加上简单的组合规律(如引擎透过接口来呼叫轮胎),也形成了「一致的造形」。

图-10、汽车设计者采纳EIT一致造形
典型的EIT造形,<E&I>是一起设计的,<I>的定义权属于<E>设计团队的。从<E>的视角来看,此<I>是<E>所专属的。从<T>的视角来看,此<I>是各<T>所共享的;<E>也是各<T>所共享的;也就是说两者都是通用性的。<E&I>表达了各买主(或客户)的通用性功能,而<T>则表达了各买主的特殊性需求。通用性的<I>,有两层意义:1) 容纳买主需求(或选择)的未来变化,或容纳新买主的新选择;2) 限制买主的选择范围。例如,买主买了车子之后,未来随时可以改变选择(沙滩、公路或高山),展现出序中有乱的设计。例如,买主未来决定将车子要到沙滩上跑时,就更换新轮胎,如下图。

图-11、EIT:一致造形又包容变化
只要我们心怀EIT造形,就可以感受到汽车设计者基于「序中有乱」思维,进行减法设计,以简单的序(即接口<I>)来包容<T>的多变,以便面对<信息的有限性>的挑战。由于这些都是集装箱的设计之道,于是我们就运用Doicker集装箱概念来把这些相关事物的变化(乱),加以包装于三个集装箱里。

图-12、以集装箱<隔离>变化
每一个集装箱都呈现序中有乱,它们把变化封装起来,让您拥有确定感,并通过秩序来掌握变化,就比较不会害怕变化。因而,才敢大胆去作加法,创造无限的新奇组合。例如,有一位客人想要购买一辆吉普车。汽车制造者就遵循集装箱设计之道,心怀着EIT造形,就迅速组合出一辆新车卖给客人了。

图-13、瞬间实时组合
这C和P两个集装箱都实现了序中有乱的减法设计,让EIT集装箱很容易把两者组合起来成为和谐的整体。此外,EIT集装箱又包容内部EIT造形的无限变化,更加展现出无限新奇的加法设计。有了EIT造形的减法设计,让人们拥有确定感,不会害怕变化,而大幅激发出与生俱来的加法设计能力和创意。
Docker + EIT造形
在需求、数据和软件愈来愈碎片化的趋势下,集装箱包装了微服务(Micro-Service)成为主流。这些微服务在运行时间(Run-time)经常需要动态性组合成为各式各样的App来支撑企业多变的业务流程(Business Process)。举例来说,在游戏业务里,有三个业务模块,分别由不同团队开发,并各自打包成为Docker集装箱,如下图:

图-14、一款游戏里的三个模块
在这个游戏里,玩家操控飞机,携带摄像头(Camera)飞越港口上空,游戏画面会出现摄像头所拍到的景象。如下图:

图-15、飞到港口上空所拍摄到的景象
这三项企业模块之间的动态結合(Association)关系,并非布署时间(Deployment-time)的相依性,並不属于Docker核心所掌管的范围。当飞机继续飞到另一个城市上空时,将会动态結合另一个集装箱的<城市3D图>,飞机所携带的摄像头会拍到新的城市景象。如下图:

图-16、飞到另一个城市上空所拍摄到的景象
顾名思义,”Docker”是:码头上的集装箱搬运工。Docker不仅要把集装箱搬运到不同平台(码头),还要搭配业务模块的动态组合而及时建立或删除集装箱,例如,飞机即将到某个城市上空之前,必须及时将<城市3D图>集装箱建立起来;此外,也可能立即将<港口3D图>集装箱删除了。这意味着,在App执行期间(Run-time)可能些业务模块必须及时将最新状态通知Docker Engine核心。但是,又不能让各业务模块开发者都随意使用Docker Engine的API,以避免各业务模块里处处充斥着Docker API,业务模块才不会被Docker绑住。此时,EIT造形就派上用场了。首先,来看看如何将<无人飞机>和<摄像头>两个Docker集装箱的组合起来,并能包容未来环境的变化。

图-17、Docker集装箱的简单组合
于是,心中想到又要面对<信息的有限性>的挑战:无法预知未来,又不想冻结未来。此时,EIT造形就浮上心头,设计一个EIT集装箱来组合,如下图:

图-18、创造一个EIT集装箱
心中当然很清楚,这EIT集装箱里含有一个单纯的EIT造形。

图-19、EIT集装箱的内部设计
现在看看如何面对动态组合的情境。当飞机继续飞到另一个城市上空时,将会动态结合另一个集装箱的<城市3D图>,飞机所携带的摄像头会拍到新的城市景象。此时,在软件系统里,就瞬间改变EIT集装箱里的EIT造形,以便适应环境变化而展现出新奇的组合。
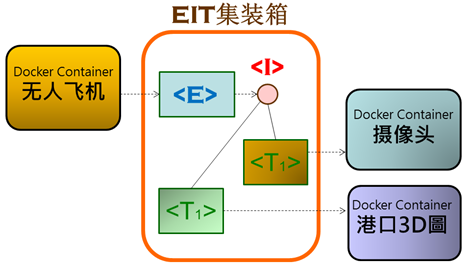
图-20、EIT集装箱内部的千变万化
EIT造形与原子造形是一样的,像氢原子(H)和氧原子(O)两者有一致的造形,内涵各不一样。EIT造形的内部元素,以及元素的不同组合,赋予各个造形不同的内涵。所以上图-19和图-20里的两个EIT集装箱,两者有一致的造形,而内涵不同。这符合集装箱的设计之道:一致造形、包容变化。
4. 软件范例:EIT造形的实践
兹拿Android的SurfaceView框架为例。摄像头(Camera)能透过镜头去取得视像,然后将视像传递到SurfaceView显示窗口里呈现出来。所以,我们必须将<手机屏幕>和<摄像头>两个模块组合起来,并能包容未来环境的变化。

图-21、手机屏幕与Camera的组合
Android是基于Linux操作系统而开发的,也是基于Linux进程(Process)的沙盒隔离策略的。同样的,Docker集装箱也是基于Linux进程的沙盒隔离机制的。因此, Android和Docker的系统架构里蕴含了高度的一致性:都采取基于进程的集装箱思维。于是,可以设计两个类:SurfaceView与Camera。其分别在不同的Android进程(或Docker集装箱)里执行。

图-22、建立两个软件集装箱
同樣地,心中想到又要面对<信息的有限性>的挑战:无法预知未来,又不想冻结未来。此时,EIT造形就浮上心头,设计一个EIT集装箱来组合,如下图:

图-23、创建一个EIT集装箱
同樣的,心中当然很清楚,这EIT集装箱里含有一个单纯的EIT造形。

图-24、最典型的EIT造形设计
集装箱的设计之道:一致造形、包容变化。其意味着,一样造形,内涵可千变万化。例如上图的EIT造形,可以弹性变化如下图:

图-25、集裝箱內部的变化
在我写的另一篇文章:《Android和Docker的一致架构设计:分合自如的设计模式》里,我提到过,善用EIT造形,可创造美妙的应变效果。例如,两支App分别跑在两个不同的集装箱里,然后透过 Docker平台的通信协议(如REST)来交互信息。有一天,维运人员为了节省资源而把这两地集装箱里的两支App加以<合并>到同一个集装箱里运行,却不需要开发者更改两支App的代码。所以上图里的三个集装箱,我们可以将它们合并成一个集装箱。
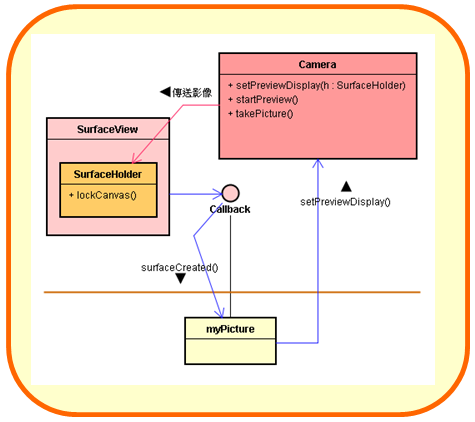
图-26、集装箱外部变化:合并集装箱
设计师将SurfaceView与Camera两者的相依性(Dependency)降低,成为疏结合(Loosely Coupled),预留了弹性,让业主在稍后出现时,能有决策的空间,并委托App开发者把其决策写在App子类(如myPicture)里。这是Android设计师采取EIT的<一致造形>来包容业主商业决策的变化。
5、结语:集装箱之道、单纯与美丽
在我写的《思考软件,创新设计:A段架构师的思考技术》一书里,我特別闡述如何发挥软件集装箱的对称、单纯和美丽。依据爱因斯坦《相对论》的说法:
“事物看上去是相对的,可是不要被善变的外貌所愚弄了。”摘自 K. C. Cole的The Universe and the Teacup一书。
简而言之,当某事物在某种变化中不变,则称该事物具有对称性(Symmetry)。也就说,当你把某个对象变换后,其形状不变的话,就找到一种对称性了。例如一个正方形,当它被旋转90度之后,就形状而言,你看不出有什么地方不同;此时你已经看到不变性了,因此找到对称性了。所以,寻找对称性也就是寻找不变性(Invariance)。当你发现两个事物是对称的,就会想到两个事物幕后的不变性,它蕴含单纯和美丽。因此会想到如何表达出这个单纯美丽的密切联系。例如,当我们把一堆鞋子放入一只集装箱里;经由轮船运抵对岸之后,将鞋子倒出来,成为空集装箱。接着,又把一堆袜子放入该只集装箱里。此时,可观察到鞋子和袜子两项内涵(Content)的对称性,其幕后的集装箱造形(Form)的不变性,也蕴含了单纯和美丽。 ~ End ~
高(焕堂)老师与您分享顶级的视频课程,请点击:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~



