活用<BP算法的黃金三公式>
By 高煥堂
一、前言
在上一篇文章《AI機器學習的黃金三公式》裏,已經說明瞭,學習AI的BP算法有兩個途徑:
途徑-1. 像牛頓一樣的科學家,會去用數學證明 F = ma。如果您是AI算法和模型的科學家,才需要懂微積分去證明AI算法裡的常用簡單公式。
途徑-2. 像一般的學生們的學習物理時,常先記住F=ma 或 E = MC^2的簡單公式,然後一邊應用,一邊領會,最後才去研讀牛頓F=ma的推導過程。
在AI的NN方面也是一樣的。在我出版的《不編程,而學AI:Excel+TensorFlow》一書裡(P.243~245)有如下的圖:
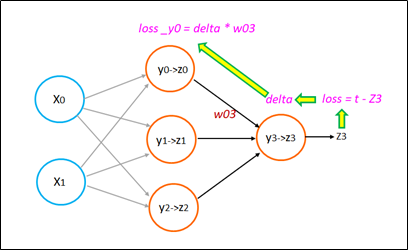
首先您只需知道(先記住即可)NN的Layer與Layer之間BP傳播算法的非常簡單的公式。然後,再去探究delta與error(又稱loss)的關係。請留意,我這裏的error(即loss)不是L()損失函數的值,而這error只是單純指誤差值(t - z3)而已。也就是:
error = t - z3
接著,您只要弄懂delta與error之間的關係,就OK啦。此時,請您先記住簡單公式(慢慢再求深入理解):
delta = error * z3 * (1- z3)
於是,您就輕易弄懂了以上的圖了,也就是知道了Layer與Layer之間的BP(反向傳播)之關係。
接下來,剩下一步,就是要知道如何更新Weights值。在我的《不編程,而學AI:Excel+TensorFlow》一書裡(P.246)有一張圖:
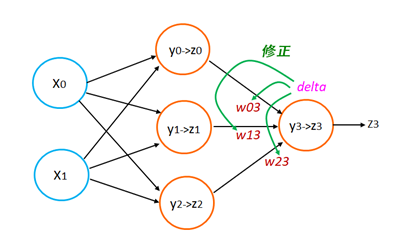
基於剛才已經理解的delta來修正W 就行了。此時請您先記住修正W的公式:
w03 += delta * z0
w13 += delta * z1
w23 += delta * z2
于是,大功告成了,完成了Z3神經元的BP計算了,不亦簡乎、不是樂乎?
二、應用於CNN的卷積層
現在,舉一個最簡單的範例,更容易凸顯如何將上述的NN(神經網路)的BP算法直接應用於CNN的卷積層上,就能够一石兩鳥,同時理解一般NN,又能應用CNN。這個簡單的範例是:
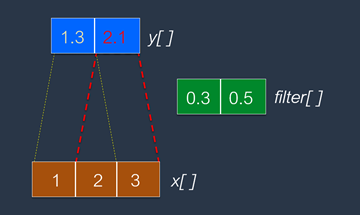
把它對應到神經元模型上,如下圖:
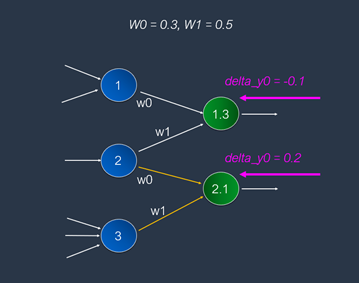
在CNN的BP算法裏,後續層會回傳error值。由于CNN卷積層最常用的激活函數是ReLU。采取ReLU激活函數時,loss值等于delta值(暫時不必問爲什麽,後續有閑情時再去探究即可)。從上圖可以看到了,後續輸出層回傳delta值(已經使用第1公式,從error轉換成為delta值了)是[-0.1, 0.2]。運用上一篇文章所提供的第2公式,很容易從這個delta[]值,反向推導出前一層的error值,並算出delta值,如下:

就得到了delta_x值:[0.03, 0.01, 1.0],如下:
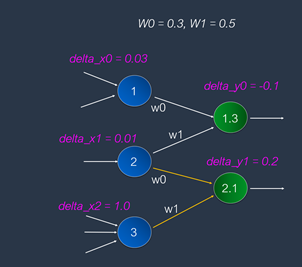
接下來,再運用上一篇文章所提供的第3公式,很容易來修正這卷積層的weight[ ]值了。如下:

以及:

就得到了新的w值:[0.6, 0.9]了。
~ END ~
*** 歡迎參閱 高煥堂的4本AI書籍:

==> 返回首頁


