AI機器學習的BP黃金三公式

AI機器學習的BP黃金三公式

by 高煥堂 

misoo.tw@qq.com

2019_08_06

 

1. 記住第一個公式：delta = z * (1 - z) * error

 這項<BP算法黃金三公式>名稱是我提出的，幷不見得人人都贊同，但是它的確可以非常有效地簡化AI的教學與學生們的學習途徑。雖然看起來這些式子，如：delta = z * (1-z) * error，看來很複雜。其實，只要您不掉入數學推導的細節，它是非常簡單可愛的。其中，error就是預測值與實際值(標簽)的落差值。所以：

   delta = z * (1 - z) * error

   其中的z *(1-z)就是Sigmoid激活函數的導數。將它記住了之後，做些變化。例如，當激活函數改爲ReLU時，其導數爲1或0，此時，這個黃金公式就變成爲：

   delta = loss (或 0)

所以先記住： delta =  z * (1 - z) * error。就能隨著兩種變因而舉一反三了。其變因有二：1)損失函數(Loss Function)；2)激活函數(Activation Function)。例如，最常見的損失函數是MSE(即均方誤差)或SSE(誤差平方和)；而最常見的激活函數是Sigmoid函數。 

2.  逐漸孰悉它的變化：

   例如，改變一下，把損失函數改爲交叉熵時，這標準公式會變成什麽? 再如，改變一下，把激活函數改爲ReLU時，這標準公式會變成什麽? 然後，再改變一下，把激活函數改爲Softmax時，這標準公式會變成什麽? 如此，就很輕易地掌握NN的BP算法的任督之脉了。如此，一切變化盡在其中，就不必去糾纏于對損失函數的偏微分推倒細節了，也就是不必去糾纏于梯度向量的推算細節了，它們都在這簡單公式裡了。 

3. 就像牛頓力學的公式：F = ma

  這項 delta = z * (1 - z) * error 公式，就像幾何學裏的圓形面積公式：Area = PI * r^2 一樣，人人朗朗上口，也像牛頓力學的F = ma公式，或像愛因斯坦的 E = MC^2 質能變換公式一樣，記住它，活用它，然後才漸漸去理解它是如何導出的，甚至許多人一輩子也都不去煩惱它們是如何推導出來的。

4.  三個基本公式

  許多人都可以直接記住它、活用它，總共三個簡單公式：

• 第1公式：delta =  z * (1 - z) * error
• 第2公式：error_prev = W * delta
• 第3公式：dw = X_prev * delta

  這三個公式如同牛頓力學三大定律公式。基于這項基礎知識，就能非常迅速地算出NN, CNN, RNN等神經網絡模型的AI機器學習流程了。 

5.  範例一：解析Python代碼

  例如，在我所撰寫的《Python 與TensorFlow結合》一書裡，有一段代碼：

for i in range(500):

    hy = x.dot(w1)

    hz = relu(hy)

    oy = hz.dot(w2)

    oz = sigmoid(oy)

 

    # Compute and print loss

    L = np.square(t - oz).sum()

    print(i, L)

 

    # Backprop to compute gradients of w1 and w2 with respect to loss

    error = t - oz

    delta = oz * (1-oz) * error

    dw2 = hz.T.dot(delta)

    error_h = delta.dot(w2.T)

    delta_h = error_h.copy()

    delta_h[h < 0] = 0

    dw1 = x.T.dot(delta_h)

 

    # Update weights

    w1 += learning_rate * dw1

    w2 += learning_rate * dw2

 

  這是兩層的NN模型，損失函數L()是SSE，隱藏層的激活函數是ReLU，輸出層則是Sigmoid激活函數。所以，

      delta = oz * (1-oz) * error

   和  delta_h = loss_h.copy()

      delta_h[h < 0] = 0

 

就是第一公式的呈現。至於，

       error_h = delta.dot(w2.T)

是第二公式的呈現。 再來，

       dw2 = hz.T.dot(delta)

       dw1 = x.T.dot(delta_h)

則是第三公式的呈現。

       w1 -= learning_rate * dw1

       w2 -= learning_rate * dw2

    幾乎所有複雜NN的BP算法，都是這三個簡單公式的華麗呈現而已。拿這三個公式去對應和詮釋別人的算法或程序代碼，就不必去追踪別人的程序邏輯，而一目了然。而且對或錯，一清二楚。

 

6.  範例二：解析Torch代碼

   再如，引用 ：http://www.sohu.com/a/291959747_197042網頁裡提供的一份代碼： 

## sigmoid activation function using pytorch

def sigmoid_activation(z):

return 1 / (1 + torch.exp(-z))

 

## activation of hidden layer

z1 = torch.mm(x, w1) + b1

a1 = sigmoid_activation(z1)

 

## activation (output) of final layer

z2 = torch.mm(a1, w2) + b2

output = sigmoid_activation(z2)

loss = y - output

 

## function to calculate the derivative of activation

def sigmoid_delta(x):

return x * (1 - x)

 

## compute derivative of error terms

delta_output = sigmoid_delta(output)

delta_hidden = sigmoid_delta(a1)

 

## backpass the changes to previous layers

d_outp = delta_output * loss

loss_h = torch.mm(d_outp, w2.t())

d_hidn = delta_hidden * loss_h

 

learning_rate = 0.1

w2 += torch.mm(a1.t(), d_outp) * learning_rate

w1 += torch.mm(x.t(), d_hidn) * learning_rate

b2 += d_outp.sum() * learning_rate

b1 += d_hidn.sum() * learning_rate

 

其中的指令：

    d_outp = delta_output * loss

    d_hidn = delta_hidden * loss_h

就是第一公式的呈現。而，

    loss_h = torch.mm(d_outp, w2.t())

就是第二公式的呈現。再來，

    w2 += torch.mm(a1.t(), d_outp) * learning_rate

    w1 += torch.mm(x.t(), d_hidn) * learning_rat

就是第三公式的呈現。于是，三個基本公式就清晰地浮現出來了，也由于很孰悉這三個公式了，就很容易理解這些程序碼的涵意，也能輕易判斷程序是否正確。

 

7. 範例三：解析NN模型圖

    例如，有一個CNN模型的架構圖：

  

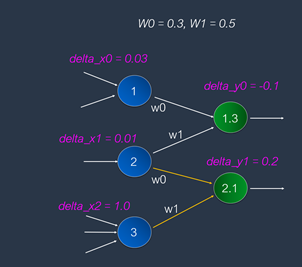
  基于已經熟悉的BP三公式，就清晰知道這些數字之間的相關性了。例如，此圖裡的藍色神經元屬於輸入層，綠色神經元屬於卷積層。目前已經知道了：

      delta_y0 = -0.1

     delta_y1 = 0.2

運用上述的<BP三公式>，就能反向推演出來delta_x0、delta_x1和delta_x2了。很容易展開如下的計算過程：

 

    這就是所謂的反向傳播(BP)：讓敏感度(即 delta值)，就如同海水的漣漪效應一般，從輸出層逆向傳播到各層，來更新權重值(含B值)。

 

8. 結語

   學習AI的BP算法有兩個途徑：

途徑-1. 像牛頓一樣的科學家，會去用數學證明 F = ma。如果您是AI算法和模型的科學家，才需要懂微積分去證明AI算法裡的常用簡單公式。

途徑-2. 像一般的學生們的學習物理時，常先記住F=ma 或 E = MC^2的簡單公式，然後一邊應用，一邊領會，最後才去研讀牛頓F=ma的推導過程。

==> 返回首頁

~ End ~