浅谈导数
简介
又是一个新学年,靠近高二新生的不只有开学还有导数()
你时常发现,数学书上的讲解往往是“一般的”,对于很爱问为什么的你肥肠不友好
所以这是一个你可以当做导数入门看的文章,当然也会有一些书本上原本没有的内容,希望可以帮助各位
在课本上没有详细讲的东西会有解释?
会不自觉提到很多本来不用提的东西(?)
如果你是求导大师就已经可以走了,这里没有啥新东西()
会用到同济的高等数学作为扩展()
简要框架
因为我知道一个人看一个自己不适应的逻辑顺序的文章时有多么不理解,我先简要说一说我的行文框架。
如果你不喜欢,我个人推荐可以选择看\(B\)站大学上的教程,特别是 \(\text{3Blue1Brown}\)(?)
我们简单看一看课本是怎么引入导数,又是怎么一层一层递进地介绍的:
- 5.1. 导数的概念和意义
- 5.1.1. 变化率问题
- 5.1.2. 导数的概念及其几何意义
- 5.2. 导数的运算
- 5.2.1. 基本初等函数的导数
- 5.2.2. 导数的四则运算法则
- 5.2.3. 简单复合函数的导数
- 5.3. 导数的应用
- 5.3.1. 与函数单调性的关系
- 5.3.2. 与函数的极值与最大(小)值的关系
那么因为是应试教育(),我们就按照这个顺序来。
而某些人强调过 “数学就是玩概念的”,所以一般来说我会先把一部分中的概念顺序拎出来聊,再讲记号,再讲具体的内容。
正文部分
\(\mathbb{I.}\) 引入导数的概念
此内容对应\(课本 5.1 节\)
涉及概念
大家都学过高一物理那这个 瞬时速度 的概念我就不讲了(
那么课本就这么引入了这个问题,说明我们 确实 需要这么一个东西帮助我们更好的解决现实问题
这里也进而为后面合理引入 瞬时变化量 的概念设下伏笔
大家都学过高一物理那这个 任意曲线的切线 这个概念我也不讲了(
这里课本也是用了高一物理里面教的定义方法,也是合理的
然后课本就通过给这两个问题找了一个共同点:都是用 平均变化率 逼近 瞬时变化率
然后特殊问题普通化,就有了这个 导数,又称作 瞬时变化率 的东西
令我比较不解的是他定义完了导数之后又回去定义了切线?你上面不是刚刚讲过吗??
然后课本用切线把导数这个概念与几何相结合
然后课本对你说:
在一堆题目里面你可以看出来,\(y=f(x)\) 在 \(x=x_0\) 处求导的过程中,\(x=x_0\) 时,\(f'(x)\) 是一个唯一确定的数. 这样,当 \(x\) 变化时,\(y=f'(x)\) 就是 \(x\) 的函数,我们把它
称为 \(y=f(x)\) 的 导函数,简称 导数.
所以各位明晰一下导数有两个概念,一个是 “导函数” 的简称,一个是 “瞬时变化率” 的别称
换个比较方式:一个是函数,一个是这个函数某个位置具体的值
注意区分(虽然不考)
数学记号
好了,概念知道了,接下来讲一讲记号
导数(瞬时变化量)的记号还是常见的,记做 \(f'(x_0)\) 或者是 \(y'|_{x=x_0}\)
其实这个 \(f'(x_0)\) 已经是在套用导数(导函数)的记号了,也就是 \(y=f'(x)\)
\(\Delta x,\Delta y\) 都可以简单理解成这两个变量的有向变化量,是存在正负的
重头戏还得是 \(\lim\) 和 \(\rightarrow\),这个记号基本上预示着你学的数学不再那么天真,具体了
这两个记号在课本里面有些突然:两个都是在说明意义之后简单引入的,有可能吓到人(
我们在写 \(x \rightarrow p\) 的时候,翻译成简体中文就是:“变量 \(x\) 无限趋近于常量 \(p\)”,
而我们在写 \(\lim\limits_{x \rightarrow p} f(x)=l\) 的时候,适当翻译就是:“当 \(x \rightarrow p\) 时,\(f(x) \rightarrow l\)”
具体内容
极限相关知识
这一部分只想看导数的或者学过的可以跳过,不影响
(等一下我翻一下同济的高等数学)
为什么有极限这个东西呢?
因为有些时候明明这个函数的图像很优美,就是那里缺了一个点,例如 \(f(x)=\dfrac{\sin x}{x}\) 在 \(x=0\) 处明明很平滑,应该非常自然的等于 \(1\) ,但是它就是在 \(x=0\) 处没有意义:
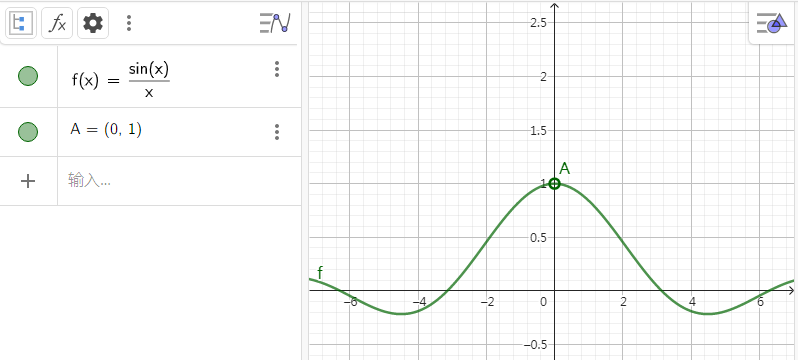
(此图片利用Geogebra绘制,图中 \(x\) 轴单位长度 \(:y\) 轴单位长度 \(=\pi:1\))
又好比 \(f(x)=\dfrac 1x\) 的最两端看着就像 \(0\),但是他永远都不是 \(0\),你也用不了其他具体的数字来说
因为极限可以让某一些数学家能意会的东西更加具体顺带满足一些强迫症数学家的私心,所以它诞生了
所以注意:\(\lim\limits_{x\rightarrow p}f(x)\) 是否存在与 \(f(p)\) 是否有意义无关
对于上面的某些定义或者意义,某些比较较真的同学可能会问:如果说:“自变量 \(x\) 无限趋近于常量 \(p\)”,那么这个 “无限趋近” 的具体定义怎么表述?
其实是一个不错的问题,因为你马上会意识到有三种趋近的方式:
在数轴上 \(x\) 逼近 \(p\) 的过程中:
- 始终有 \(x<p\)(此时记做 \(x\rightarrow p^{-}\),\(\lim\limits_{x\rightarrow p^{-}}f(x)\) 称为左极限)
- 始终有 \(x>p\)(此时记做 \(x\rightarrow p^{+}\),\(\lim\limits_{x\rightarrow p^{+}}f(x)\) 称为右极限)
- \(x\) 在 \(p\) 两侧反复横跳(就是刚刚讲的 \(x \rightarrow p\))
所以有一个分类的定义:
对公式过敏者慎重选看
我偷个懒没问题吧(有个前提是\(\exists \delta'>0,f(x)\) 在 \(P_i(\delta')\) 上有定义
\(\lim\limits_{x\rightarrow p_i}=A\iff\forall \varepsilon >0,\exists \delta \in(0,\delta'),\left[\forall x\in P_i(\delta),|f(x)-A|<\varepsilon\right]\),其中 \(p_i\iff\begin{cases}p&i=1\\p^{+}&i=2\\p^{-}&i=3\end{cases}\),\(P_i(\delta)=\begin{cases}(p-\delta,p)\cup(p,p+\delta)&i=1\\(p,p+\delta)&i=2\\(p-\delta,p)&i=3\\\end{cases}\)
有人会说:诶这几个玩意区分他干嘛
but这点确实需要在我们的考虑范围之内,因为这个要点不仅 受到函数定义域的约束 ,还与 因变量最后趋向的值 有关
例如前者,我们在遇到函数 \(f(x)=x^2,x\in (0,+\infin)\) 时,你发现求 \(\lim\limits_{x\rightarrow 0} f(x)\) 你只能从右边逼近,它只存在一个 \(\lim\limits_{x\rightarrow 0^{+}}\),所以极限是否存在受到函数定义域的约束
而后者也可以举例解释,比如 \(f(x)=\operatorname{sgn}(x)\cdot\left(x^2+\dfrac 12\right)\),其中 \(\operatorname{sgn}(x)=\begin{cases}\frac{|x|}{x}&x\neq 0\\0&\text{otherwise}\end{cases}\)
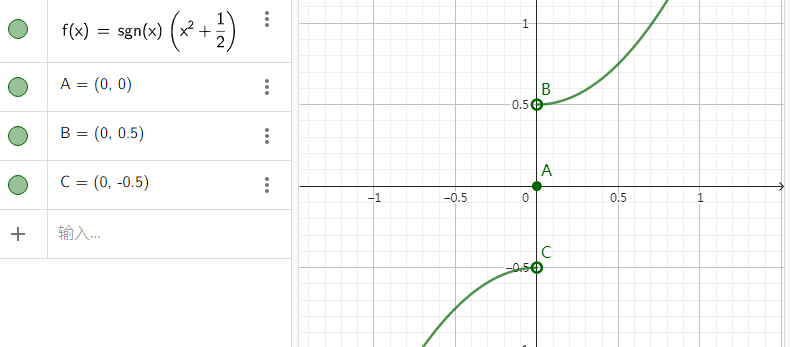
这个函数在 \(x=0\) 处的左右极限大家都能意会出来吧?一个是 \(-\dfrac 12\),一个是 \(\dfrac 12\)
那它为什么没有极限也能意会到了吧?
这两个例子也可以解释上面提到的
\(\lim\limits_{x\rightarrow p}f(x)\) 是否存在与 \(f(p)\) 是否有意义无关
第一个例子中 \(f(0)\) 无意义(不在定义域中)而 \(\lim\limits_{x\rightarrow 0}f(x)=0\)
第二个例子中 \(f(0)=0\) 但是 \(\lim\limits_{x\rightarrow 0}f(x)\) 不存在
\(\lim\limits_{x\rightarrow p}\) 中这个 \(p\) 还可以换成 \(+\infin,-\infin,\infin\),定义当中换成相应的区间即可
其中第三种情况的极限存在当且仅当第一和第二种情况的极限存在且相等
所以一共有六种不同的极限,而对于其中任意一种,都有一些共同的性质,包括四则运算性质(以极限为例):
若 \(\lim\limits_{x\rightarrow p}f(x)=A\) 且 \(\lim\limits_{x\rightarrow p}g(x)=B\),
那么有:\(\lim\limits_{x\rightarrow p}f(x)\plusmn g(x)=A\plusmn B\)
\(\lim\limits_{x\rightarrow p}f(x)\cdot g(x)=A\cdot B\)
\(\lim\limits_{x\rightarrow p}\dfrac{f(x)}{g(x)}=\dfrac AB\ (B\neq 0)\)
还有迫敛性(同样以极限为例):
若 \(\lim\limits_{x\rightarrow p}f(x)=\lim\limits_{x\rightarrow p}g(x)=A\),并且 \(\forall x\in (p-\delta,p)\cup(p,p+\delta)(\delta >0),f(x)\le h(x)\le g(x)\)
则有 \(\lim\limits_{x\rightarrow p}h(x)=A\)
先扯到这里,到需要的时候再进一步补充
你问我怎么算极限?好比求导,背一堆基本的,再用四则运算性质转换,特殊的情况可以用 洛必达法则(先不讲)
当然高中里如果这个地方本来就有定义的话直接带就好了,除非这个地方的极限不存在
但是这个东西高中也不考啊
导数的基础定义和几何意义
如果 \(f(x)\) 在区间 \((x_0-\delta,x_0+\delta)(\delta >0)\) 内有定义
\(f'(x_0)=\lim\limits_{\Delta x\rightarrow 0} \dfrac{\Delta y}{\Delta x}=\lim\limits_{\Delta x\rightarrow 0} \dfrac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\)
其实和极限类似,导数也有左右导数……可以自己写写式子,下个定义试试看
\(\lim\) 中的这个式子当做求瞬时速度时长得和平均速度的式子差不多,可以看出导数的现实意义就是 平均增长率的极限
这个式子还可以写成 \(\dfrac{f(x_0+\Delta x)-f(x_0)}{(x_0+\Delta x)-x_0}\),看着就像是 \((x_0,f(x,0)),(x_0+\Delta x,f(x_0+\Delta x))\) 两个点连接所成的直线的斜率,\(\Delta x\rightarrow 0\) 时两个点不断接近,也就变成了 切线的斜率,也就是 导数的几何意义,即 \(y=f(x)\) 的图像在 \(x=x_0\) 处的位置的切线斜率大小
\(\mathbb{II.}\) 导数的运算
此内容对应\(课本 5.2 节\)
涉及概念
这一部分没有什么概念了
因为开始吃名为计算的硬骨头
数学记号
嗯,最多是 \((\sin x)'\) 这一种?
具体内容
一部分基本初等函数的导数
注:我知道可以用一堆不知道哪里来的极限求出来,但我真的不想把极限讲的太细,所以找了一些较能绕过极限的方法
当然还是有些无法避免,或者确实重要的
我们首先来看看一些基本的初等函数的导数长什么样子
-
常函数 \(f(x)=c\),\(f'(x)=0\)
这个书上够清楚了,偷懒了(
-
幂函数 \(f(x)=x^n\ (n\in \mathbb{R})\),\(f'(x)=nx^{n-1}\)
嗯,课本很厉害,他教会我用了 \(5\) 个特例就可以找到规律
大家都知道杨辉三角,也就是组合数吧?
大家也知道 \((a+b)^n=\sum\limits_{i=0}^n\dbinom{n}{i}a^ib^{n-i}(n\in \mathbb{Z}^+)\) 吧?
嗯?你不知道?
考虑带有 $a^i$ 每一项系数的组合意义因为有乘法分配律,和式相乘拆开括号后的结果,相当于是每一次在一个括号里面只选择一个项,再把所有选出来的项乘起来,最后把所有情况相加
就好比 \((a+b)(c+d)=ac+ad+bc+bd\),相当于枚举了所有的情况
因为乘法有交换律,所以乘的顺序没有影响
问题转化为:在所有情况中选且只选出了 \(i\) 个 \(a\) 的情况数,不考虑顺序
这不就是 \(n\) 个里面选 \(i\) 个的组合数吗?\(\dbinom{n}{i}\) 秒了
又由于 \(n\) 个里面选 \(i\) 个,剩下的 \(n-i\) 个一定全是 \(b\),所以 \(b\) 的幂次是 \(n-i\)
我们可亲可敬的数学家们(应该是某位名人)在延拓了组合数的范围之后,这个 \(n\) 不再受限于 \(\mathbb{Z}^+\) 之中,而是有:\((a+b)^n=\sum\limits_{i=0}^n\dbinom{n}{i}a^ib^{n-i}(n\in \mathbb{R})\),并且 \(\forall n\in \mathbb{R},\dbinom{n}{0}=1,\dbinom{n}{n-1}=\dbinom{n}{1}=n\)
而按照导数的定义展开后:
\(\begin{aligned} f'(x)&=\lim\limits_{\Delta x\rightarrow 0}\dfrac{(x+\Delta x)^n-x^n}{\Delta x}\\ &=\lim\limits_{\Delta x\rightarrow 0}\dfrac{\sum\limits_{i=0}^{n-1}\dbinom{n}{i}x^i{\Delta x}^{n-i}}{\Delta x}\\ &=\lim\limits_{\Delta x\rightarrow 0}\sum\limits_{i=0}^{n-1}\dbinom{n}{i}x^i{\Delta x}^{n-i-1}\\ &=\sum\limits_{i=0}^{n-1}\dbinom{n}{i}x^i\lim\limits_{\Delta x\rightarrow 0}{\Delta x}^{n-i-1}&(极限的四则运算规则)\\ \end{aligned}\)
我们知道 \(\forall n>0,f(x)=x^n\) 在 \((0,+\infin)\) 上单调递增
所以在 \(n>0\) 时,\(\lim\limits_{\Delta x\rightarrow 0} (\Delta x)^n=0\)
而 \(n=0\) 时,\(\lim\limits_{\Delta x\rightarrow 0} (\Delta x)^n=1\)
\(\forall i\in [0,n-1],n-i-1\ge 0\)
所以对于这个 \(\sum\) 里的每一项,只有 \(i=n-1\) 这一项不为 \(0\)
所以 \(f'(x)=\dbinom{n}{n-1}x^{n-1}=nx^{n-1}\)
-
正弦函数 \(f(x)=\sin x\),\(f'(x)=\cos x\)
你学过一个公式叫做和角公式
\(\begin{aligned} f'(x)&=\lim\limits_{\Delta x\rightarrow 0}\dfrac{\sin(x+\Delta x)-\sin x}{\Delta x}\\ &=\lim\limits_{\Delta x\rightarrow 0}\dfrac{\sin x \cos \Delta x +\sin \Delta x \cos x -\sin x}{\Delta x}\\ &=\sin x\lim\limits_{\Delta x\rightarrow 0}\dfrac{\cos \Delta x-1}{\Delta x}+\cos x\lim\limits_{\Delta x\rightarrow 0}\dfrac{\sin \Delta x}{\Delta x} \end{aligned}\)
嗯……剩下的这两个部分虽然可以画图像
\(\lim\limits_{\Delta x\rightarrow 0}\dfrac{\sin \Delta x}{\Delta x}=1\)
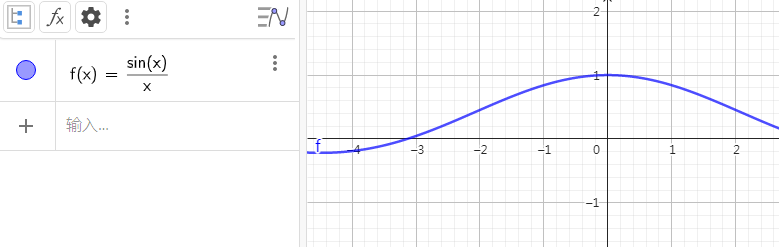
\(\lim\limits_{\Delta x\rightarrow 0}\dfrac{\cos \Delta x-1}{\Delta x}=0\)
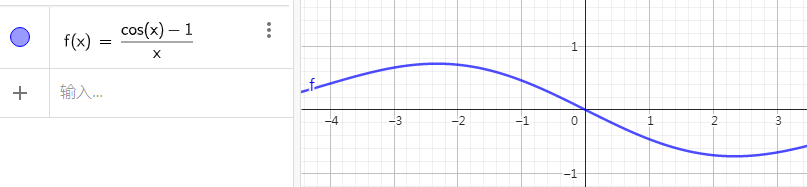
但手画这两个图像对于人类来说还是太困难了一点
所以小证一下:
(1) \(\lim\limits_{x\rightarrow 0}\dfrac{\sin x}{x}=1\)
观察到结论 \(\forall x\in \left(0,\dfrac{\pi}{2}\right),\sin x<x<\tan x=\dfrac{\sin x}{\cos x},\cos x>0\)
观察不到?
可以回高一补一补,如果你是高一及以下当我没说放一张图作无字证明:
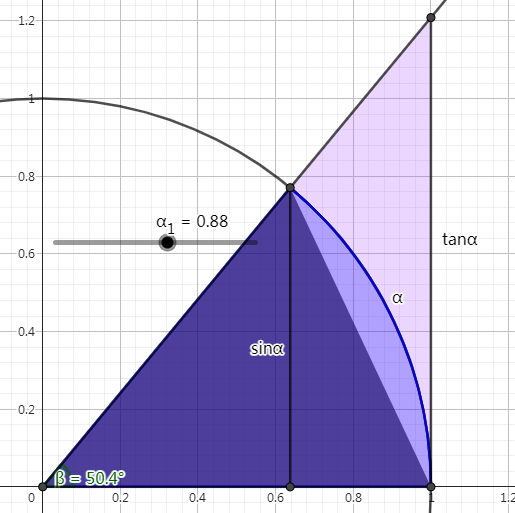
所以有 \(\forall x\in \left(0,\dfrac{\pi}{2}\right),x\cos x<\sin x<x\)
变成 \(\forall x\in \left(0,\dfrac{\pi}{2}\right),\cos x<\dfrac{\sin x}{x}<1\)
\(\begin{aligned} \because&\lim\limits_{x\rightarrow 0} \cos x=\lim\limits_{x\rightarrow 0} 1=1\\ \therefore&\lim\limits_{x\rightarrow 0} \dfrac{\sin x}{x}=1 &(极限的迫敛性) \end{aligned}\)
(2) \(\lim\limits_{x\rightarrow 0}\dfrac{\cos x-1}{x}=0\)
先把上面的式子拆成单项,考虑到有:\(\cos x=1-2\sin^2\dfrac{x}{2}\)
\(\begin{aligned} \lim\limits_{x\rightarrow 0}\dfrac{\cos x-1}{x}&=\lim\limits_{x\rightarrow 0}\dfrac{-2\sin^2\frac{x}{2}}{x}\\ &=-\lim\limits_{x\rightarrow 0}\dfrac{\sin^2\frac{x}{2}}{\frac{x}{2}}\\ &=-\lim\limits_{x\rightarrow 0}\dfrac{\sin^2\frac{x}{2}}{\left(\frac{x}{2}\right)^2}\cdot \dfrac x2\\ &=-\lim\limits_{x\rightarrow 0}\left(\dfrac{\sin\frac{x}{2}}{\frac{x}{2}}\right)^2\cdot \lim\limits_{x\rightarrow 0}\dfrac x2\\ &=-1\cdot 0\\ &=0 \end{aligned}\)
上面两个极限的证明结束了,代回原来的式子后可知 \(f'(x)=\cos x\)
-
余弦函数 \(f(x)=\cos x\),\(f'(x)=-\sin x\)
你以为我要用 \(\cos x\) 的和角公式?
\(f(x)=\cos x=\sin(x-\frac{\pi}{2})\)
相当于 \(g(x)=\sin x\) 的图像整体向左平移 \(\frac{\pi}{2}\) 个单位长度
那么原来是在 \(x=x_0\) 处的切线同样平移,此时 \(x=x_0-\frac{\pi}{2}\) 而切线斜率不变
所以 \(f'(x-\frac{\pi}{2})=g'(x)=\cos x\)
\(f'(x)=\cos (x+\frac{\pi}{2})=-\sin x\)
-
自然指数函数 \(f(x)=e^x\),\(f'(x)=e^x\)
学到导数了,怎么能没有 \(e\) 呢?
我们直接展开:
\(\begin{aligned} f'(x)&=\lim\limits_{\Delta x\rightarrow 0}\dfrac{e^{(x+\Delta x)}-e^x}{\Delta x}\\ &=\lim\limits_{\Delta x\rightarrow 0}e^x\cdot \dfrac{e^{\Delta x}-1}{\Delta x}\\ &=e^x\lim\limits_{\Delta x\rightarrow 0}\dfrac{e^{\Delta x}-1}{\Delta x}\\ \end{aligned}\)
额,剩下的这部分虽然也可以画图像:
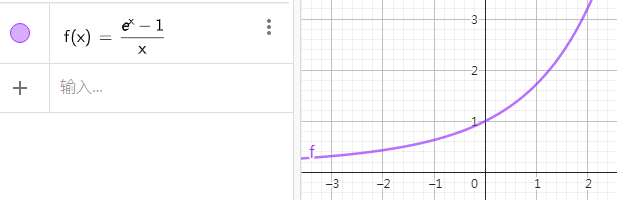
手画对于人类来说还是太困难了一点
证明:\(\lim\limits_{x\rightarrow 0}\dfrac{e^x-1}{x}=1\)
考虑换元,令 \(u=e^x-1\),则有 \(x=\ln (u+1)\),且可知 \(x\rightarrow 0\) 时 \(u \rightarrow 0\)
\(\begin{aligned} \lim\limits_{x\rightarrow 0}\dfrac{e^x-1}{x}&=\lim\limits_{u\rightarrow 0}\dfrac{u}{\ln(u+1)}\\ &=\lim\limits_{u\rightarrow 0}\dfrac{1}{\ln\left[(u+1)^\frac 1u\right]}\\ \end{aligned}\)
\(\ln\) 里面这个东西实际上就是 \(e=\lim\limits_{n\rightarrow \infin} \left(1+\dfrac{1}{n}\right)^u=\lim\limits_{n\rightarrow 0} (1+n)^\frac 1n\)
所以 \(\lim\limits_{x\rightarrow 0}\dfrac{e^x-1}{x}=\lim\limits_{u\rightarrow 0}\dfrac{1}{\ln e}=\lim\limits_{u\rightarrow 0} 1=1\)
代回去,可以知道 \(f'(x)=e^x\)
我知道初等函数没有列举完你写别急
导数的四则运算法则
我们肯定不想对于所有的函数都算极限,更希望通过已知的函数的导数推理出其他一般函数的导函数
所以我们考虑:对于函数 \(f(x)\) 和 \(g(x)\) 有什么可能的变换
-
我会加减法!
\(\begin{aligned} \left[f(x)\plusmn g(x)\right]'&=\lim\limits_{\Delta x\rightarrow 0} \dfrac{[f(x+\Delta x)\plusmn g(x+\Delta x)]-[f(x)\plusmn g(x)]}{\Delta x}\\ &=\lim\limits_{\Delta x\rightarrow 0} \dfrac{f(x+\Delta x)-f(x)}{\Delta x} \plusmn \lim\limits_{\Delta x\rightarrow 0} \dfrac{g(x+\Delta x)-g(x)}{\Delta x}\\ &=f'(x)\plusmn g'(x) \end{aligned}\)
所以有:\([f(x)\plusmn g(x)]'=f'(x)\plusmn g'(x)\)
-
我会乘法!
\(\begin{aligned} \left[f(x)g(x)\right]'&=\lim\limits_{\Delta x\rightarrow 0} \dfrac{f(x+\Delta x)g(x+\Delta x)-f(x)g(x)}{\Delta x}\\ &=\lim\limits_{\Delta x\rightarrow 0} \dfrac{f(x+\Delta x)g(x+\Delta x)-f(x)g(x+\Delta x)+f(x)g(x+\Delta x)-f(x)g(x)}{\Delta x}\\ &=\lim\limits_{\Delta x\rightarrow 0} \dfrac{f(x+\Delta x)g(x+\Delta x)-f(x)g(x+\Delta x)}{\Delta x}+\lim\limits_{\Delta x\rightarrow 0} \dfrac{f(x)g(x+\Delta x)-f(x)g(x)}{\Delta x}\\ &=\lim\limits_{\Delta x\rightarrow 0}g(x+\Delta x)\cdot \lim\limits_{\Delta x\rightarrow 0} \dfrac{f(x+\Delta x)-f(x)}{\Delta x}+f(x) \lim\limits_{\Delta x\rightarrow 0} \dfrac{g(x+\Delta x)-g(x)}{\Delta x}\\ &=g(x)f'(x)+f(x)g'(x) \end{aligned}\)
所以有: \([f(x)g(x)]'=f(x)g'(x)+g(x)f'(x)\)
特别的,\(f(x)=C\),即 \(f(x)\) 为常函数的时候有:
\([Cg(x)]'=Cg'(x)+[C]'g(x)=Cg'(x)\)
-
我会除法!
\(\begin{aligned} \left[\dfrac{f(x)}{g(x)}\right]'&=\lim\limits_{\Delta x\rightarrow 0} \dfrac{\dfrac{f(x+\Delta x)}{g(x+\Delta x)}-\dfrac{f(x)}{g(x)}}{\Delta x}\\ &=\lim\limits_{\Delta x\rightarrow 0} \dfrac{f(x+\Delta x)g(x)-f(x)g(x+\Delta x)}{\Delta x\cdot g(x)\cdot g(x+\Delta x)}\\ &=\lim\limits_{\Delta x\rightarrow 0} \dfrac{\dfrac{f(x+\Delta x)-f(x)}{\Delta x}\cdot g(x)-f(x)\cdot \dfrac{g(x+\Delta x)-g(x)}{\Delta x}}{g(x)\cdot g(x+\Delta x)}\\ &=\dfrac{f'(x)g(x)-f(x)g'(x)}{g(x)^2} \end{aligned}\)
所以有: \(\left[\dfrac{f(x)}{g(x)}\right]'=\dfrac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}\)
-
我会复合函数!
\(\begin{aligned} \left[f(g(x))\right]'&=\lim\limits_{\Delta x\rightarrow 0} \dfrac{f(g(x+\Delta x))-f(g(x))}{\Delta x}\\ &=\lim\limits_{\Delta x\rightarrow 0} \dfrac{f(g(x+\Delta x))-f(g(x))}{g(x+\Delta x)-g(x)}\cdot \dfrac{g(x+\Delta x)}{\Delta x}\\ &=\lim\limits_{\Delta x\rightarrow 0} \dfrac{f(g(x+\Delta x))-f(g(x))}{g(x+\Delta x)-g(x)}\cdot \lim\limits_{\Delta x\rightarrow 0} \dfrac{g(x+\Delta x)}{\Delta x}\\ &=f'(g(x))g'(x)\\ \end{aligned}\)
所以有: \([f(g(x))]'=f'(g(x))g'(x)\)
提醒一下,\([f(g(x))]'\) 表示的是 \(f(x)\) 和 \(g(x)\) 的复合函数的导数,而 \(f'(g(x))\) 表示的是 \(f(x)\) 的导数和 \(g(x)\) 的复合函数
除法法则的另一种理解方式:
\(\begin{aligned} 令 h(x)&=x^{-1},有 h'(x)=-x^{-2}\\ \left[\dfrac{f(x)}{g(x)}\right]'&=\left[f(x)h(g(x))\right]'\\ &=f(x)\cdot \left[h(g(x))\right]'+f'(x)h(g(x))\\ &=f(x)h'(g(x))g'(x)+\dfrac{f'(x)}{g(x)}\\ &=\dfrac{-f(x)g'(x)}{g(x)^2}+\dfrac{f'(x)g(x)}{g(x)^2}\\ &=\dfrac{f'(x)g(x)-f(x)g'(x)}{g(x)^2} \end{aligned}\)
-
我会反函数!
记 \(f(x)\) 的反函数为 \(f^{-1}(x)\)
有:\(\begin{cases} y=f^{-1}(x)\\ x=f(y) \end{cases}\)
\(\begin{aligned} \left[f^{-1}(x)\right]'&=\lim\limits_{\Delta x\rightarrow 0} \dfrac{\Delta y}{\Delta x}\\ &=\lim\limits_{\Delta x\rightarrow 0} \dfrac{1}{\frac{\Delta x}{{\Delta y}}}\\ &=\dfrac{1}{\lim\limits_{\Delta y\rightarrow 0} \frac{\Delta x}{{\Delta y}}}\\ &=\dfrac{1}{f'(y)}\\ &=\dfrac{1}{f'(f^{-1}(x))} \end{aligned}\)
所以有: \(\left[f^{-1}(x)\right]'=\dfrac{1}{f'(f^{-1}(x))}\)
另一部分基本初等函数的导数
讲了这些有用的导数运算法则,我们就能继续推其他基本初等函数的导数了
反三角函数的导数我应该不用讲
其他像 \(\cot\) 这种三角函数的导数我应该也不用讲
-
自然对数函数 \(f(x)=\ln x\),\(f'(x)=\dfrac{1}{x}\)
\(\begin{aligned} 令 g(x)&=e^x\\ \because f(x)&=g^{-1}(x)\\ \therefore f'(x)&=\dfrac{1}{g'(f(x))}\\ &=\dfrac{1}{e^{ln x}}=\dfrac 1x \end{aligned}\)
-
指数函数 \(f(x)=a^x\),\(f'(x)=a^x \ln a\)
\(\begin{aligned} f(x)&=a^x=e^{x\ln a}\\ f'(x)&=e^{x\ln a}\cdot (x\ln a)'=a^x \ln a \end{aligned}\)
-
对数函数 \(f(x)=\log_a x\),\(f'(x)=\dfrac 1{x\ln a}\)
\(\begin{aligned} f(x)&=\log_a x=\dfrac{\ln x}{\ln a}\\ f'(x)&=\dfrac 1{\ln a}(\ln x)'=\dfrac 1{x\ln a} \end{aligned}\)
-
正切函数 \(f(x)=\tan x\),\(f'(x)=\dfrac 1{\cos^2 x}\)
\(\begin{aligned} f(x)&=\dfrac{\sin x}{\cos x}\\ f'(x)&=\dfrac {\cos x(\sin x)'-\sin x(\cos x)'}{\cos^2 x}\\ &=\dfrac{\cos^2 x+\sin^2 x}{\cos^2 x}\\ &=\dfrac 1{\cos^2 x} \end{aligned}\)
双曲函数
等等这是啥?为啥突然不讲导数了?
这个双曲函数和三角函数的相似性太令我震惊了一点……权当拓展,可以略过
先来看看什么是双曲函数:
\(\begin{aligned} \operatorname{sh} x&=\dfrac{e^x-e^{-x}}2 &(奇函数)\\ \operatorname{ch} x&=\dfrac{e^x+e^{-x}}2 &(偶函数)\\ \operatorname{th} x&=\dfrac{\operatorname{sh} x}{\operatorname{ch} x}=\dfrac{e^x-e^{-x}}{e^x+e^{-x}} \end{aligned}\)
那为什么我们说双曲函数和三角函数之间具有相似性呢?来看一些例子:
\(\begin{array}{c||c} \operatorname{ch}^2 x-\operatorname{sh}^2 x=1&\cos^2 x+\sin^2 x=1\\ \operatorname{sh} 2x=2\operatorname{ch} x\operatorname{sh} x&\sin 2x=2\sin x\cos x\\ \operatorname{ch} 2x=\operatorname{ch}^2 x+\operatorname{sh}^2 x&\cos 2x=\cos^2 x-\sin^2 x\\ \operatorname{th} x=\dfrac{\operatorname{sh} x}{\operatorname{ch} x}&\tan x=\dfrac{\sin x}{\cos x}\\ \operatorname{sh}(x+y)=\operatorname{sh} x\operatorname{ch} y+\operatorname{ch} x\operatorname{sh} y&\sin(x+y)=\sin x\cos y+\cos x\sin y\\ \operatorname{sh}(x-y)=\operatorname{sh} x\operatorname{ch} y-\operatorname{ch} x\operatorname{sh} y&\sin(x-y)=\sin x\cos y-\cos x\sin y\\ \operatorname{ch}(x+y)=\operatorname{ch} x\operatorname{ch} y+\operatorname{sh} x\operatorname{sh} y&\cos(x+y)=\cos x\cos y-\sin x\sin y\\ \operatorname{ch}(x-y)=\operatorname{ch} x\operatorname{ch} y-\operatorname{sh} x\operatorname{sh} y&\cos(x-y)=\cos x\cos y+\sin x\sin y \end{array}\)
看出了什么?
这两玩意真的只是在公式上相差了几个正负号啊!
等等,既然刚刚讲了导数,怎么能不讲导数的相似性
\(\begin{array}{c||c} (\operatorname{sh} x)'=\operatorname{ch} x&(\sin x)'=\cos x\\ (\operatorname{ch} x)'=\operatorname{sh} x&(\cos x)'=\sin x\\ \end{array}\)
那么你我不免会问是为什么。
emm...你有没有看过一个叫做Alan的人做的名为“火柴人 VS 数学”的视频?
那你是不是记得有一个公式叫做欧拉公式:\(e^{i\pi}=-1\)?
合理而言他的扩展长这样:\(e^{ix}=\cos x+i\sin x\)
所以从中你或许能够看出来双曲函数和三角函数的些许关系
先来看 \(\operatorname{sh} x\) 和 \(\sin x\)
\(\begin{aligned} \operatorname{sh} ix&=\dfrac{e^{ix}-e^{-ix}}2\\ &=\dfrac{(\cos x+i\sin x)-(\cos -x+i\sin -x)}2\\ &=\dfrac{\cos x+i\sin x-\cos x+i\sin x}2\\ &=i\sin x \end{aligned}\)
所以 \(\operatorname{sh} ix=i\sin x\),即:\(\sin x=\dfrac{\operatorname{sh} ix}i=-i\operatorname{sh} ix\),\(\operatorname{sh} x=-i\sin ix\)
和谐
再是 \(\operatorname{ch} x\) 和 \(\cos x\)
\(\begin{aligned} \operatorname{ch} ix&=\dfrac{e^{ix}+e^{-ix}}2\\ &=\dfrac{(\cos x+i\sin x)+(\cos -x+i\sin -x)}2\\ &=\dfrac{\cos x+i\sin x+\cos x-i\sin x}2\\ &=\cos x \end{aligned}\)
所以 \(\cos x=\operatorname{ch} ix\),\(\operatorname{ch} x=\cos ix\)
同样和谐,同时有 \(\operatorname{th} x=\dfrac{\operatorname{sh} x}{\operatorname{ch} x}=\dfrac{-i\sin ix}{\cos ix}=-i\tan ix\)
举个相似性推导的例子,比如:\(\operatorname{ch}^2 x-\operatorname{sh}^2 x=1\),这个式子可以直接代入定义证明
还可以这么干:
\(\begin{aligned} \cos^2 x+\sin^2 x=1&\iff \operatorname{ch}^2 ix + i^2 \operatorname{sh}^2 ix=1\\ &\iff \operatorname{ch}^2 ix-\operatorname{sh}^2 ix=1\\ &\iff \operatorname{ch}^2 x-\operatorname{sh}^2 x=1 \end{aligned}\)
换个例子,比如:\(\sin 2x=2\sin x\cos x\) 和 \(\cos 2x=\cos^2 x-\sin^2 x\),这个式子也可以直接代入定义证明
还可以这么干:
\(\begin{aligned} \sin 2x=2\sin x\cos x&\iff -i\operatorname{sh} 2ix=2\cdot-i\operatorname{sh} ix\operatorname{ch} ix\\ &\iff \operatorname{sh} 2ix=2\operatorname{sh} ix\operatorname{ch} ix\\ &\iff \operatorname{sh} 2x=2\operatorname{sh} x\operatorname{ch} x\\ \cos 2x=\cos^2 x-\sin^2 x&\iff \operatorname{ch} 2ix=\operatorname{ch}^2 ix-(i\operatorname{sh} ix)^2\\ &\iff \operatorname{ch} 2ix=\operatorname{ch}^2 ix+\operatorname{sh}^2 ix\\ &\iff \operatorname{ch} 2x=\operatorname{ch}^2 x+\operatorname{sh}^2 x \end{aligned}\)
其他的大家感兴趣可以自己试试
牛顿迭代
就书上这个例子,作了解已经够了
至于深入吗……左转B站3b1b走起
\(\mathbb{III.}\) 导数的应用
此内容对应\(课本 5.3 节\)
涉及概念
新增了一个极值,或者说,局部最大(小)值
数学记号
同样没有
具体内容
导数与函数的单调性
我们知道,在区间 \([a,b]\) 上的单调性,例如递增,可以表示成:\(\forall x_1,x_2\in [a,b],x_1<x_2\Rightarrow f(x_1)<f(x_2)\)
我们还知道不等式具有传递性,所以:
\(\forall x_1,x_2\in \mathbb{R} \wedge x_1<x_2,\Big[\exists \{a_n\},a_1=x_1,a_n=x_2,\forall i\in [1,n)\cap \mathbb{Z},f(a_i)<f(a_{i+1})\Big]\Rightarrow f(x_1)<f(x_2)\)
人话说就是:对于任意的一对数 \(x_1,x_2\) 有 \(x_1<x_2\),存在一列以 \(x_1\) 开头,\(x_2\) 结尾的数,相邻两项对应的函数值都呈现 \(f(a_i)<f(a_{i+1})\) 的不等式,那么由不等式的传递性可知 \(f(x_1)<f(x_2)\)
那么我们想到:如果 \(\forall x\in (a,b),f'(x)>0\):
\(\begin{aligned} \forall x\in (a,b),f'(x)>0&\iff\forall x\in (a,b),\lim\limits_{\Delta x\rightarrow 0}\dfrac{f(x+\Delta x)-f(x)}{\Delta x}>0\\ &\iff\forall x\in (a,b),\lim\limits_{\Delta x\rightarrow 0}[f(x+\Delta x)-f(x)]\Delta x>0\\ &\iff\forall x\in (a,b),\lim\limits_{\Delta x\rightarrow 0^{+}}[f(x+\Delta x)-f(x)]\Delta x>0\\ &\iff\forall x\in (a,b),\lim\limits_{\Delta x\rightarrow 0^{+}}[f(x+\Delta x)-f(x)]>0\\ &\iff\forall x,y\in (a,b),y>x\Rightarrow f(y)>f(x)\\ &\iff y=f(x)在区间(a,b)内单调递增 \end{aligned}\)
单调递减的情况相似
导数与函数的极值
极值点的导数为 \(0\) 可以尝试主观理解()
额,书上给了一个左右侧导数与 \(0\) 比大小看是不是极值点,为什么呢?
高数上的一副插图直观解释了这个必要不充分的条件:
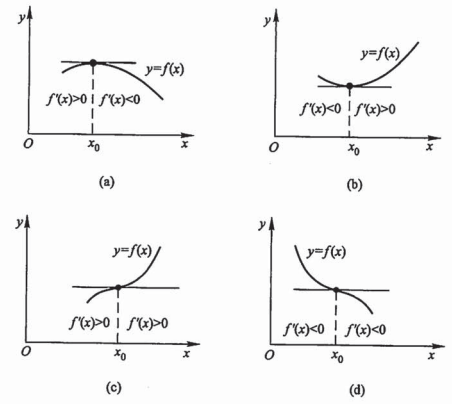
而最值只能是极值或者端点的值
最后书中给出了一个研究函数的方式:根据 \(f(x)\) 的图象判断 \(f(x)\) 的性质,根据 \(f'(x)\) 的性质画出 \(f(x)\) 的图象
不是你在这里套娃呢

尾声
好了,这里就是所有作者认为值得一写的课本上所提的导数部分内容
有什么建议都可以在评论区提,作者后续也会进一步完善


 浙公网安备 33010602011771号
浙公网安备 33010602011771号