数学之地
让我们来锻练数学的功底吧!
\(\mathfrak{P.S.}\)我并不认为你们傻,我只是想要随便写写而已
——\(\color{LimeGreen}{\text{SmallBlack}}\)
章节:
\(\mathcal{I}\) 几何板块
\(\ \ \ \ \mathbb{ .}\) 几何入门
\(\ \ \ \ \ \ \ \ \mathtt{I.}\) 点与线
\(\ \ \ \ \mathbb{I}\).直线的相交
\(\ \ \ \ \ \ \ \ \mathtt{I.}\) 相交
\(\ \ \ \ \ \ \ \ \ \ \ \ \mathfrak{i.}\)推论:
\(\ \ \ \ \ \ \ \ \ \ \ \ \mathfrak{ii.}\)证明:
\(\ \ \ \ \ \ \ \ \mathtt{II.}\)特殊情况:
\(\ \ \ \ \mathbb{II}\).平行线的性质及判定
\(\ \ \ \ \ \ \ \ \mathtt{I.}\)定义:
\(\ \ \ \ \ \ \ \ \mathtt{II.}\)基本事实:
\(\ \ \ \ \ \ \ \ \mathtt{III.}\)推论:
\(\ \ \ \ \ \ \ \ \mathtt{IV.}\)证明:
\(\ \ \ \ \ \ \ \ \ \ \ \ \mathfrak{(1)}\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \mathfrak{(2)}\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \mathfrak{(3)}\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \mathfrak{(4)}\)
直接裂开
\(\mathcal{I.}\)几何板块
\(\mathbb{\ .}\) 几何入门
(不是我的\(\LaTeX\)炸了,是罗马数字里本来就没有0(雾))
- 我们把点,线,面,体这\(\mathtt{4}\)个整数维空间(对应\(\mathtt{0}-\mathtt{3}\)维)称为几何图形,其中"体"称作立体图形,其余三类称作平面图形,我们重点考虑平面图形.
\(\mathtt{I.}\) 线
\(\mathfrak{i.}\)类型
一般的,线分为三类:
\(\text{线}\begin{cases}\text{直线}\\\text{射线}\\\text{线段}\end{cases}\)
\(\mathfrak{ii.}\)特点:
| 线的类型 | 区别 | 读法 | 方向性 |
|---|---|---|---|
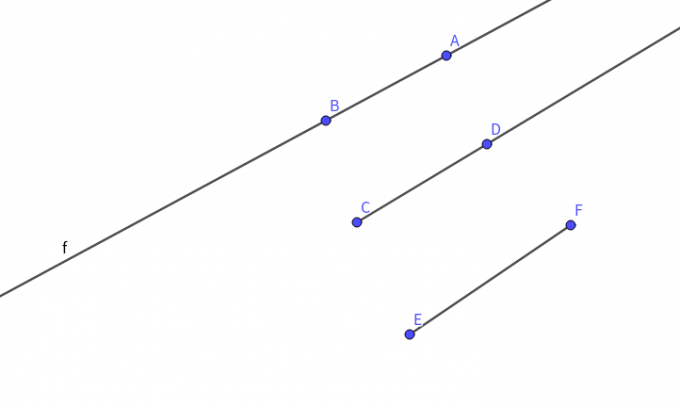
| 直线 | 无端点 | 直线\(AB\),直线\(BA\),直线\(f\) | 无 |
| 射线 | 有一个端点 | 射线\(CD\) | 有 |
| 线段 | 有两个端点 | 线段\(EF\),线段\(FE\) | 无 |
\(\mathfrak{iii.}\)相关定义:
- 点\(C\)把线段\(AB\)分为两条线段\(AC\)与\(BC\),如果\(AC=BC\),那我们称点\(C\)是线段\(AB\)的中点
\(\mathfrak{iv.}\)基本事实:
\(\mathtt{1.}\) 两点确定一条直线
\(\mathtt{2.}\) 两点之间线段最短
\(\mathtt{II.}\) 角
- 角是两条有公共端点的射线组成的图形,这个公共端点称作这个角的顶点,角也可以看作是一条射线绕他的端点旋转后形成的图形,起始的位置称作角的始边,终止的位置称作角的终边。
\(\mathfrak{i}.\) 表示方式
我们使用\(\angle\)($\angle$)来表示角
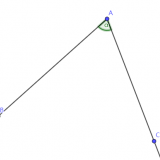
\(\mathtt{1.}\) 使用三个大写字母表示,如图1,可表示为\(\angle BAC\)
\(\mathtt{2.}\) 在不会引发歧义的情况下,我们使用这个角顶点的字母表示这个角,如图1,可表示为\(\angle A\),但图2中的\(\angle CBD\)不能使用\(\angle B\)代替,因为\(\angle B\)可能表示\(\angle ABC\)或者\(\angle CBD\)。
\(\mathtt{3.}\) 我们可以使用一个希腊字母或数字来表示一个角,如图1,可表示为\(\angle\alpha\)。
\(\mathbb{I}\).直线的相交
- 在同一平面内,两条直线有如下情况:相交或平行
\(\mathtt{I.}\) 相交
\(\mathfrak{i.}\)推论:
\(\mathtt{1.}\)对顶角相等
\(\mathtt{2.}\)邻补角互补
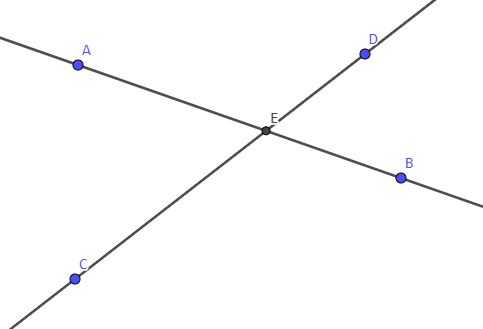
\(\mathfrak{ii.}\) 证明
如图,直线\(AB\)与直线\(CD\)交于一点\(E\),
\(\because \angle AEB=\angle CED=180^\circ\)
\(\therefore \angle AEC+\angle BEC=180^\circ\)
\(\angle CEA+\angle DEA=180^\circ\)
\(\angle AED+\angle BED=180^\circ\)
\(\angle CEB+\angle DEB=180^\circ,\)即邻补角互补
\(\therefore \angle AEC=\angle BED,\angle AED=\angle BEC,\)即对顶角相等
\(\mathtt{II.}\)垂直:
- 当两条相交的直线所构成的四个夹角中有一个为\(90^\circ\)时,我们说这两条直线互相垂直,其中一条叫做另一条的垂线,两条直线的交点被称作垂足
\(\mathbb{II}\).平行线的性质及判定
\(\mathtt{I.}\)定义:
- 在同一平面内,不相交的两条直线互相平行.
\(\mathtt{II.}\)基本事实:
\(\mathtt{1.}\)同位角相等,两直线平行。
\(\mathtt{2.}\)两直线平行,同位角相等。
\(\mathtt{III.}\)推论:
\(\mathtt{1.}\)内错角相等,两直线平行
\(\mathtt{2.}\)同旁内角互补,两直线平行
\(\mathtt{3.}\)两直线平行,内错角相等
\(\mathtt{4.}\)两直线平行,同旁内角互补
\(\mathtt{IV.}\)证明:
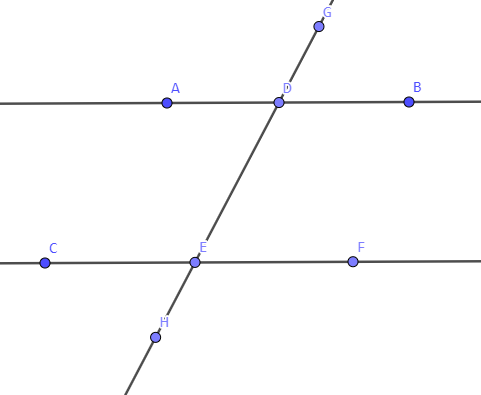
如图,在一个平面中有一条直线\(AB\)及线外一点\(C\),过\(C\)点作直线\(CF\),再画一条不与直线\(AB\)平行的直线\(GH\),分别交直线\(AB,CD\)于点\(D,E\)
\(\mathfrak{(1)}\)
已知:\(\angle ADE=\angle FED\)
求证:\(CF//AB\)
证:
\(\because AB\)与\(GH\)交于点\(D\)(已知)
\(\therefore \angle ADE=\angle BDG\)(对顶角相等)
又\(\because \angle ADE=\angle FED\)(已知)
\(\therefore \angle BDG=\angle FED\)(等量代换)
\(\therefore CF//AB\)(同位角相等,两直线平行)
\(\mathfrak{(2)}\)
已知:\(CF//AB\)
求证:\(\angle ADE=\angle FED\)
证:
\(\because CF//AB\)(已知)
\(\therefore \angle BDG=\angle FED\)(两直线平行,同位角相等)
又\(\because AB\)与\(GH\)交于点\(D\)(已知)
\(\therefore \angle ADE=\angle BDG\)(对顶角相等)
\(\therefore \angle ADE=\angle FED\)(等量代换)
\(\mathfrak{(3)}\)
已知:\(\angle ADE+\angle CED=180^\circ\)
求证:\(CF//AB\)
证:
\(\because CF\)与\(GH\)交于点\(E\)(已知)
\(\therefore \angle CED+\angle FED=180^\circ\)(邻补角互补)
又\(\because \angle ADE+\angle CED=180^\circ\)(已知)
\(\therefore \angle ADE=\angle FED\)(同角的补角相等)
\(\therefore CF//AB\)(内错角相等,两直线平行)
\(\mathfrak{(4)}\)
已知:\(CF//AB\)
求证:\(\angle ADE+\angle CED=180^\circ\)
证:
\(\because CF//AB\)(已知)
\(\therefore \angle ADE=\angle FED\)(两直线平行,内错角相等)
又\(\because CF\)与\(GH\)交于点\(E\)(已知)
\(\therefore \angle CED+\angle FED=180^\circ\)(邻补角互补)
\(\therefore \angle ADE+\angle CED=180^\circ\)(等量代换)
梅开二度
\(\text{upd:开学了,爷的青春结束了,我要开始咕咕了}\)
\\更新字典:
\\XX板块(double r)
\\r:更新进度
- 加入 相交\(1\),垂直\(0.1\),平行\(0.9\)版
- 加入 几何入门\(0.3\)
\(\mathtt{Waiting...}\)(有意见请在下方评论)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号