Baekjoon 18482 - Six Words思路

前记

你猜猜为什么只是思路

正文

题意简述

题目转送门：前提是你有账号

我们有一个函数 \(L\)，你可以向其中输入一个带点权边权的无向图 \(G\)，他会映射到另一个带点权边权的无向图 \(L(G)\)，具体方式如下：
我们记给定的图为 \(G=(V,E)\)，操作后的图为 \(G_0=(V_0,E_0)\)，那么有：

• \(G\) 中的每一条边都在 \(G_0\) 中都有唯一对应的节点，该点的点权等于该边的边权
• \(G_0\) 中两节点之间存在一条边，当且仅当这两节点在 \(G\) 中对应的边存在公共点，该边的边权等于该公共点点权

以符号化形式来说（可以忽略，格式不好或不严谨请见谅）：

• \(\exists f：E\rightarrow V_0\)
  • 或者说： \(\exists f,[\ \forall u,v\in V,[\ (u,v)\in E\iff f[(u,v)]\in V_0\wedge \operatorname{val}'(\ f[(u,v)]\ )=\operatorname e[(u,v)]\ ]\ ]\)
• \(\forall (u_1,v_1),(u_2,v_2)\in E,[\ x_1=f[\ (u_1,v_1)\ ]\wedge x_2=f[\ (u_1,v_1)\ ]\implies[\ (x_1,x_2)\in E_0 \iff [\ \exists k\in V,\{u_1,v_1\}\cap\{u_2,v_2\}=\{k\}\neq \varnothing\ ]\wedge \operatorname e'[(x_1,x_2)]=\operatorname{val}(k)\ ]\ ]\)

这就是 \(L\) 的作用

现在给定图 \(G\)，求 \(L(L(G))\) 的最小生成树的树边的边权和

其中 \(G\) 无自环无重边，
点数 \(n\) 满足 \(3≤ n ≤ 10^5\),
边数 \(m\) 满足 \(2 ≤ m ≤ \min(\frac{n(n−1)}2, 2 · 10^5)\)

样例：

思路

因为 \(n\) 已经达到了 \(10^5\) 的范围，如果我们直接暴力是骗不到多少分的，那么路就剩下两条：要么优化执行 \(L\) 的复杂度，要么寻找 \(L\) 的规律

前者很明显是不行的，因为一个度数为 \(n\) 的点在 \(L\) 函数操作后会创造出 \(\frac{n(n-1)}2\) 条新的边和 \(n\) 个度数为 \(n-1\) 的点，两次 \(L\) 操作后，如果直接暴力存储，空间首先不够用

那么就只能寻找 \(L\) 存在什么规律了

由于此题只用求最小生成树边权和，我们首先关注的肯定是边权的问题

\(L(L(G))\) 的边权从哪里来呢？是 \(L(G)\) 的点权

\(L(G)\) 的点权从哪里来呢？是 \(G\) 的边权

所以我们知道的是：\(L(L(G))\) 中出现的边权，一定是 \(G\) 中某一条边的边权转化而来的

所以 \(G\) 的点权是白给的，因为这和\(L(L(G))\)的边权没关系

而我们又知道这个 \(L(L(G))\) 有着比 \(L(G)\) 多得多的边

那么我们就知道了一个事实：如果按照边由小到大的扫描，一定是一片一片扫过去的

那么所有边权相同的边是否是聚集在一块区域内呢？我们为了优化算法，自然希望它是尽可能规律的

之前提到，一个度数为 \(n\) 的点 在 \(L\) 函数操作后会创造出 \(\frac{n(n-1)}2\) 条权值等于该点点权的新的边；或者说， 一个有 \(n\) 个节点，边权全为该点点权的完全图

而如果一条边两端点度数之和为 \(n\)，它变换后会产生一个度数为 \(n-2\) 的，权值为该边边权的点

所以我们知道： 如果单看 \(G\) 中的一条边，它会在 \(L(L(G))\) 当中对应一个边权相同的完全子图（或者说一个团）

为了后续叙述方便，我就暂且把这个东西称作 团子

嗯，这个思路确实有效，但是我们还要问，这些团子之间有什么关系？

嵌套？重合？黏连？

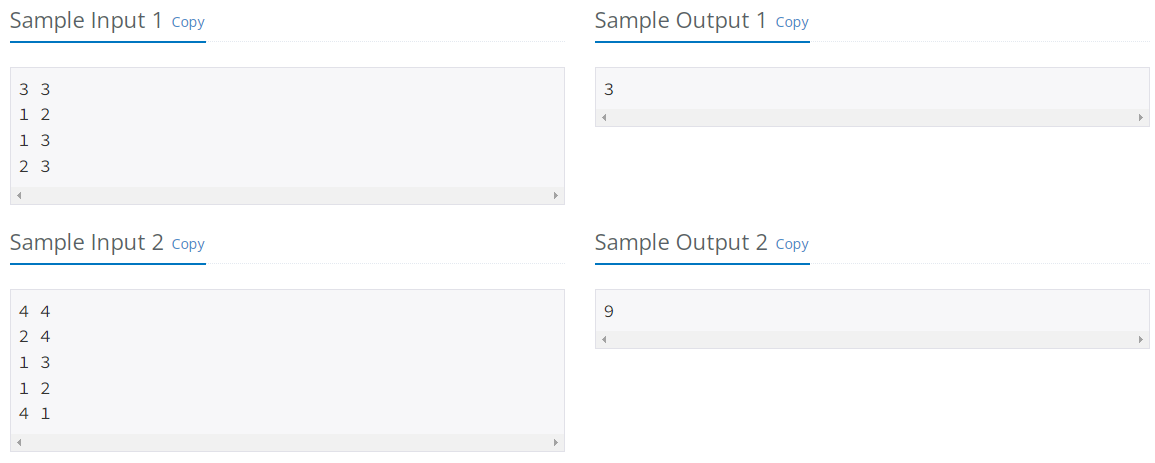
这种时候就可以写一个 \(L\) 的暴力，然后拿一个样例手玩一下，例如普通一点的样例 \(2\)：

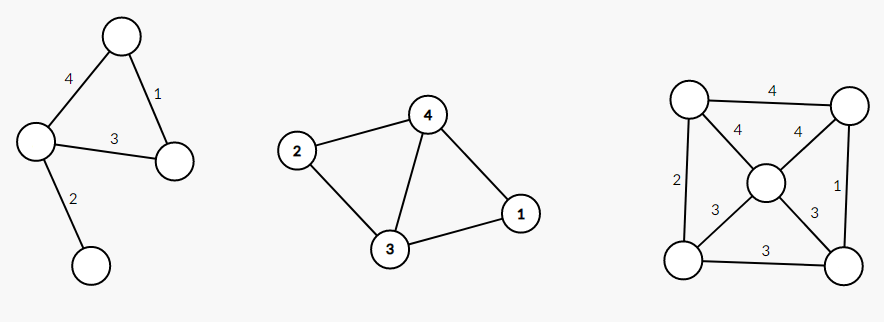
注：因为和 \(G\) 的点权无关，就把点权相关的数值擦掉了

上左图为给定的 \(G\)，向右为执行函数 \(L\) 后的结果

然后我们把 \(L(L(G))\) 里面的 团子 圈起来……

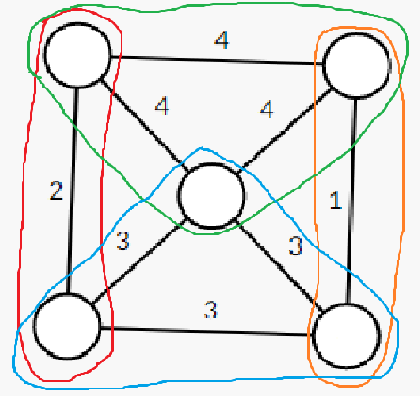
然后我们就发现了三个要点：

可以先自己再多玩几种情况，总结一下，这里是我的三个结论

1. 一个节点最多被包含在两个团子内

相应解释

因为 $L(L(G))$ 的节点对应 $L(G)$ 里的边，一条边有两个端点，而每一个 $L(G)$ 里的端点在度数大于 $2$ 时对应 $L(L(G))$ 的一个团子，所以它至多被两个完全子图包含

2. 两个不同的团子至多有一个重合的节点

相应解释

和上面大同小异，因为 $L(L(G))$ 的团子对应 $L(G)$ 里的节点，此题中两点之间至多有一条边，所以两团子至多有一个节点重合

3. 两个团子有重合点当且仅当它们在 $G$ 中所对应的边存在公共点

相应解释

根据函数 $L$ 的变换规则可以知道：$L(G)$ 中两节点之间存在边 $\iff$ 这两节点在 $G$ 中对应的边存在公共点，而从上面 $(2)$ 的解释中可知：两团子存在一个重合的节点 $\iff$ 它们在 $L(G)$ 中所对应的节点之间存在边，所以这两个命题等价

都已经到这里了，那不就是直接……

等等我们好像有一些具体的实现问题

进一步的实现

那么有实现就必须有算法的选择，有这个选择题那还是先知道数据的强度为妙

而这个 \(L(L(G))\) 的强度我不能接受（）,所以考虑在 \(G\) 上面进行操作后映射到 \(L(L(G))\) 上

为了方便处理连通性，我最后选择了 \(\text{Prim}\) 算法，具体就是在原图上跑，加入一条边就处理相应的团子内的信息

接下来就只用看团子具体怎么处理了

对于一开始大小为 \(n\) 的团子，肯定选择使用 \(n-1\) 边进行连接

那么对于之后的团子有什么需要注意的呢？

我们发现如果有好几个点已经被其他的团子访问到了，就不需要在花费一条边进行连接了

也就是说，如果当前团子有 \(n\) 个点，有 \(x\) 个已经被访问了，只需要花费 \(n-x\) 条边即可

问题又出现了：如何标记一个点被访问过了？

因为原图中一条边选取后只会影响与它有公共点的边，那只要在两个端点处打标记修改即可

接下来就是具体的代码了

现在是 \(10:46\)，我看看我什么时候打好

现在是 \(11:12\)，我打完过样例了

Code

请注意：因为这份代码是没有直接上交至Baekjoon OJ上通过题目的，所以不能保证准确性

所有代码全都是建立在上面的思路上的

如果我的思路有不当之处或者有疏漏，还请各路神仙指出

// Problem: Six Words
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// Date:2023-07-12 10:48:00
// By:SmallBlack
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;
inline long long read()
{
    long long s=0,k=1;
    char c=getchar();
    while(!isdigit(c))
    {
        k=(c=='-')?-1:1;
        c=getchar();
    }
    while(isdigit(c))
    {
        s=s*10+c-'0';
        c=getchar();
    }
    return s*k;
}
#define d read()
#define ll long long
#define Maxn 10010
#define Size 100010
#define mp make_pair
#define pb push_back
#define fi first
#define se second
vector<pair<ll,ll> >e[Size];
ll dis[Size],pre[Size];
ll tag[Size];
bool vis[Size];
ll prim(ll s)
{
    memset(dis,0x7f,sizeof dis);dis[s]=0;
    priority_queue<pair<int,int> >q;
    q.push(mp(0,s));//用二叉堆优化 Prim 至 O((n+m)logn) 完全可以接受
    ll ans=0;
    while(!q.empty())
    {
        ll u=q.top().se;q.pop();
        if(vis[u]) continue;
        vis[u]=1;
        if(u!=s)//统计原图每一条边对于L(L(G))的MST的贡献
        {
            ll sz=(ll)(e[u].size()+e[pre[u]].size()-2);
            //一条边两端点度数之和为 n，它变换后会产生一个大小为 n-2 的 “团子”
            if(ans==0) sz--;//第一个 “团子” 需要特判
            sz-=(tag[u]++)+(tag[pre[u]]++);//浅浅压行
            ans+=dis[u]*sz;
            //其实这里如果想简单点也可以直接开一个数组记录度数
            //然后打标记就相当于减两端度数了
            //或许可以稍稍减少字符数？（笑）
        }
        for(auto [v,w]:e[u])
        {
            if(!vis[v]&&w<dis[v])
            {
                dis[v]=w,pre[v]=u,
                q.push(mp(-w,v));
            }
        }
    }
    return ans;
}
int main()
{
    ll n=d,m=d;
    for(int i=1;i<=m;i++)
    {
        ll x=d,y=d;
        e[x].pb(mp(y,i)),e[y].pb(mp(x,i));
        //直接建原图后执行 Prim 算法
    }
    printf("%lld\n",prim(1));
}