决策单调性的一点理解

我做的第一道决策单调性是这道题：[Jsoi2011]柠檬。当时并不是很理解甚至根本不会决策单调性，所以随便抄抄题解就扔了，现在重新做一遍。

PS：下面的东西全是我自己瞎$YY$的，如果有错误一定要指出来啊$QwQ$

题意：给你一个长度为$n$的序列，将其分成若干段，每段选择一个数，获得这个数乘以它在这段出现次数的平方的价值。求最大总价值。

首先我们不难发现，对于选择的一段序列，头和尾的数一定是选择的数，否则我们把这个数加入其它段会使答案更优。我们设$s_i$表示第$i$个数$a_i$在之前出现的个数，那么就有这样一个状态转移方程：

$f_i=min\{f_j+a_i*(s[i]-s[j]+1)^{2}\}$

然后我们将它看成二次函数，随着$j$的增大，对于我们的决策有意义的函数集合应该是这样

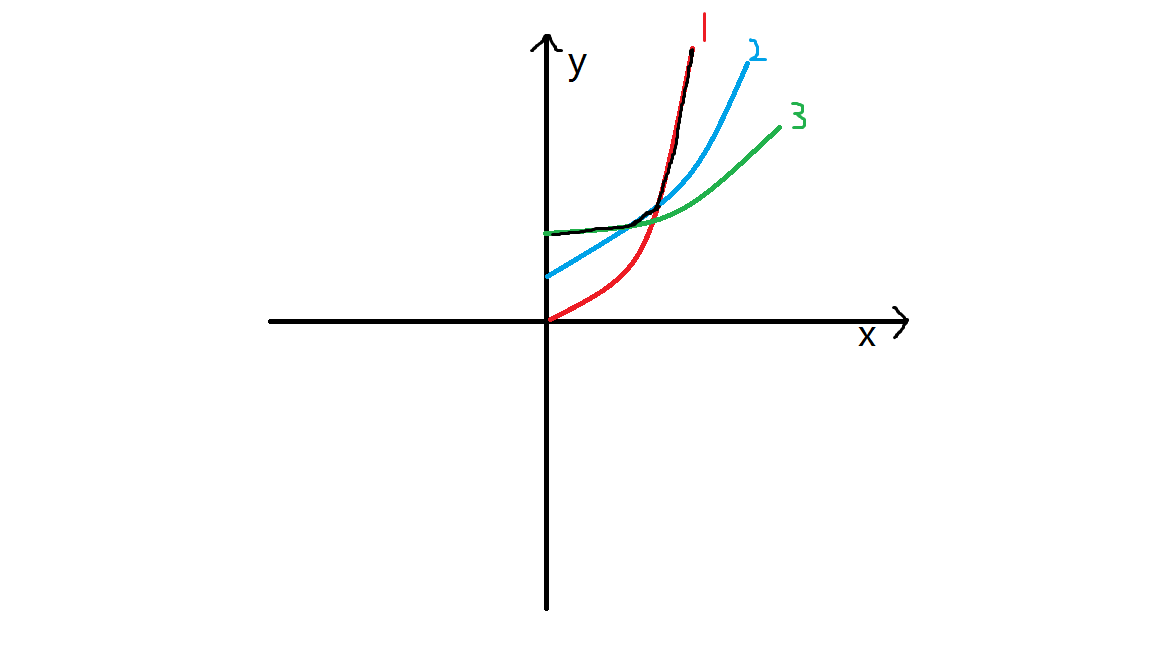
可以理解成二次函数的二次项系数随$i$增大反而减小，而常数项在不断增大

根据初中的数学知识我们知道，在两个二次函数的对称轴一侧最多可能出现一个交点

也就是说当$x=a$时第$i$个二次函数比第$j$大$(i<j)$，那么$a$之后第$i$个二次函数就一直比第$j$个大

所以如果出现下面这种情况，显然第二个二次函数就对我们的决策没有意义了

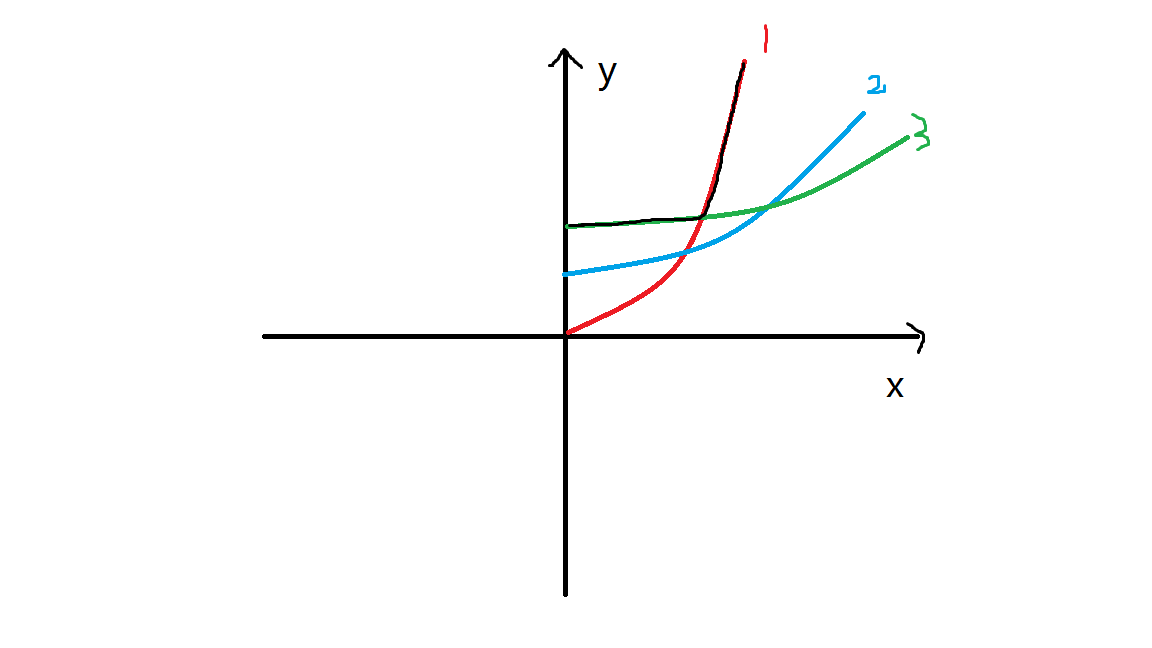
所以我们可以用一个单调栈来维护这些决策，当我们把一个新的二次函数加进栈中前，如果栈顶二次函数超过它的时间晚于第二个二次函数超过栈顶的时间，那么我们就将栈顶的二次函数弹出

当我们把一个二次函数加入栈中之后，我们还需要检查一下第二个二次函数超过栈顶二次函数的时间，如果在此之前已经超过，那么栈顶的二次函数就再也无法产生贡献了，所以我们也将它弹出即可

至于如何求这个时间，二分即可