10.6 review

Problem 1. Sum of xor

求 1 ⊕ 2 ⊕ · · · ⊕ N 的值。  A ⊕ B 即 A, B 按位异或。

Input
1 个整数 N 。
Output
1 个整数，表示所求的值。

题解：水题，有规律，虽然不会证明，先写暴力，然后输出一大串，就找到规律了。

终于可以赋上我自己的AC代码了~~2333

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cmath>
 4 #include<algorithm>
 5 using namespace std;
 6 int main()
 7 {
 8     freopen("xorsum.in","r",stdin);
 9     freopen("xorsum.out","w",stdout);
10     int x=1;
11     long long n;cin>>n;
12     if(n%4==1)
13     {
14         cout<<1<<endl;
15     }
16     else if(n%4==2)
17     {
18         cout<<n+1<<endl;
19     }
20     else if(n%4==3)
21     {
22         cout<<0<<endl;
23     }
24     else if(n%4==0)
25     {
26         cout<<n<<endl;
27     }
28     return 0;
29 }
Skyvot std

Problem 2. Sum of product

对于 A1, A2, . . . , AN ，求

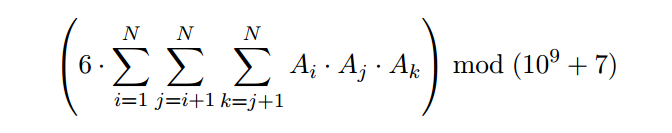
Input
第 1 行，1 个整数 N 。
第 2 行，N 个整数 A1, A2, . . . , AN 。
Output
1 个整数，表示所求的值。

Note
• 对于 30% 的数据，3 ≤ N ≤ 500；
• 对于 60% 的数据，3 ≤ N ≤ 5000；
• 对于 100% 的数据，3 ≤ N ≤ 10^6，0 ≤ Ai ≤ 10^9。

 

分析：大人，这里的6必有蹊跷。

然而，我并没有想到和这个6有什么关系的做法，相反的，我是想到了后面那一堆的求解方式——找规律

然后数据丢失了~~233就这样了。

 

posted @ 2014-11-04 19:03  Skyvot  阅读(161)  评论(0)  编辑  收藏  举报