bzoj 4822~4824 CQOI2017题解
老C的任务
题目大意:
维护一个二维平面,初始给出一些点及其权.多次询问某个矩形内的权和.
n,m <= 100000
题解:
签到题.
CDQ水一水.
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
inline void read(int &x){
x=0;static char ch;static bool flag;flag = false;
while(ch=getchar(),ch<'!');if(ch == '-') ch=getchar(),flag = true;
while(x=(x<<1)+(x<<3)+ch-'0',ch=getchar(),ch>'!');if(flag) x=-x;
}
#define rg register int
#define rep(i,a,b) for(rg i=(a);i<=(b);++i)
#define per(i,a,b) for(rg i=(a);i>=(b);--i)
const int maxn = 100010;
const int maxm = maxn;
struct Node{
int x,y;
int type,val,id;
Node(){}
Node(const int &a,const int &b,
const int &c,const int &d,const int &e){
x = a;y = b;type = c;val = d;id = e;
}
}q[maxn*6];
#define lowbit(x) (x&-x)
int n,m,mxlim;
ll c[maxn*6];int vis[maxn*6],T;
inline void modify(int x,ll d){
for(;x <= mxlim;x += lowbit(x)){
if(vis[x] == T) c[x] += d;
else c[x] = d,vis[x] = T;
}
}
inline ll query(int x){
ll ret = 0;
for(;x;x-=lowbit(x)) if(vis[x] == T) ret += c[x];
return ret;
}
int qcnt = 0;ll ans[maxm];
void solve(int l,int r){
if(l == r) return ;
int mid = l+r >> 1;
solve(l,mid);solve(mid+1,r);
++ T;rg i = l,j = mid+1,k = l;
static Node tmp[maxn*6];
while(i <= mid || j <= r){
if(i > mid || (j <= r && q[j].x < q[i].x)){
if(q[j].type == 2){
ans[q[j].id] += query(q[j].y)*q[j].val;
}
tmp[k++] = q[j++];
}else{
if(q[i].type == 1) modify(q[i].y,q[i].val);
tmp[k++] = q[i++];
}
}
rep(i,l,r) q[i] = tmp[i];
return ;
}
struct num{
int x,y,val;
}p[maxn];
struct number{
int x1,y1,x2,y2;
}nu[maxm];
int b[maxn*6],cnt;
int main(){
read(n);read(m);
rg x,y,v;
rep(i,1,n){
read(p[i].x);read(p[i].y);read(p[i].val);
b[++cnt] = p[i].y;
}
rg xx,yy;
rep(i,1,m){
read(x);read(y);read(xx);read(yy);
b[++cnt] = y;b[++cnt] = yy;
if(x > xx) swap(x,xx);
if(y > yy) swap(y,yy);
nu[i].x1 = x;nu[i].y1 = y;
nu[i].x2 = xx;nu[i].y2 = yy;
}
sort(b+1,b+cnt+1);
rep(i,1,n){
p[i].y = lower_bound(b+1,b+cnt+1,p[i].y) - b;
x = p[i].x;y = p[i].y;v = p[i].val;
q[++qcnt] = Node(x,y,1,v,0);
}
rep(i,1,m){
y = lower_bound(b+1,b+cnt+1,nu[i].y1) - b;
yy = lower_bound(b+1,b+cnt+1,nu[i].y2) - b;
x = nu[i].x1;xx = nu[i].x2;
q[++qcnt] = Node(xx,yy,2,1,i);
q[++qcnt] = Node(x-1,yy,2,-1,i);
q[++qcnt] = Node(xx,y-1,2,-1,i);
q[++qcnt] = Node(x-1,y-1,2,1,i);
}
mxlim = cnt;
solve(1,qcnt);
rep(i,1,m){
printf("%lld\n",ans[i]);
}
return 0;
}
题目: 老 C 的方块
题目大意:
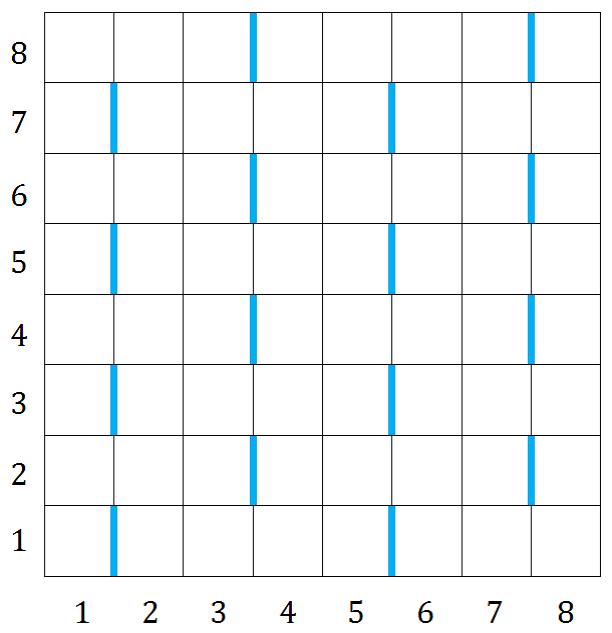
给定一个这样的R行C列网格图:加粗边称为特殊边
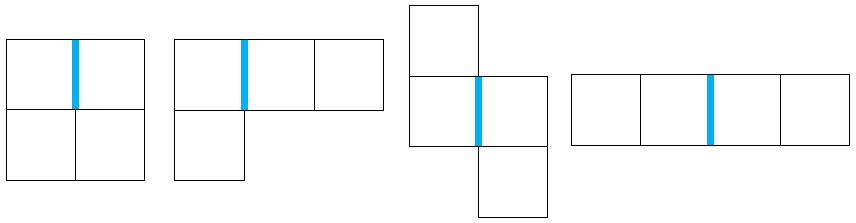
定义若出现下列情况本质相同的情况则不合法.
现在给定网格图内哪些格子是存在的及其被删除的代价共n个
最小化使得网格图合法的代价.
R,C,n <= 100000
题解:
观察所有不合法的状态.
我们发现其实就是特殊边两端不能都有大小超过2的四连块.(不经过特殊边)
所以我们可以列出一些关系:
如果将题目中给出的网格图的行列看成横纵坐标轴:(即(1,1)和(2,1)之间为特殊边)
我们可以得到这样的关系:
对于特殊边(3,2) - (4,2)来说.
如果要这条特殊边合法,那么必须是两边不能同时含有大小超过2的四连块.
那么如果我们删除(3,2)或者(4,2)这是一定满足的.
下面就是不删除(3,2)或者(4,2)的情况,那么我们知道:
要么全部删除(3,1),(2,2),(3,3),要么全部删除(4,1),(5,2),(4,3).
然后我们发现我们可以对网格图进行三色染色:建立最小割模型.
假设我们将(3,1),(2,2),(3,3)染成黑色那么(4,1),(5,2),(4,3)一定是白色.
然后将所有在特殊边两边的点染成黄色.
可以建立最小割模型:

蓝色边为删除对应格子的代价,黑色均为inf,黄色边为特殊边两边的各自的代价的最小值.
跑最小割即可.
#include <map>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
inline void read(int &x){
x=0;char ch;bool flag = false;
while(ch=getchar(),ch<'!'); if(ch == '-') ch=getchar(),flag = true;
while(x=10*x+ch-'0',ch=getchar(),ch>'!');if(flag) x=-x;
}
#define rg register int
#define rep(i,a,b) for(rg i=(a);i<=(b);++i)
#define per(i,a,b) for(rg i=(a);i>=(b);--i)
typedef pair<int,int> pa;
const int maxn = 100010;
const int inf = 0x3f3f3f3f;
struct Edge{
int to,next,cap;
}G[maxn*10];
int head[maxn],cnt = 1;
void add(int u,int v,int c){
G[++cnt].to = v;
G[cnt].next = head[u];
head[u] = cnt;
G[cnt].cap = c;
}
inline void insert(int u,int v,int c){
add(u,v,c);add(v,u,0);
}
#define v G[i].to
int dis[maxn],q[maxn],l,r,S,T;
bool bfs(){
memset(dis,-1,sizeof dis);
l = 0;r = -1;q[++r] = S;
dis[S] = 0;
while(l <= r){
int u = q[l++];
for(int i = head[u];i;i=G[i].next){
if(dis[v] == -1 && G[i].cap != 0){
dis[v] = dis[u] + 1;
q[++r] = v;
}
}
}return dis[T] != -1;
}
int dfs(int u,int f){
if(u == T || f == 0) return f;
int ret = 0;
for(int i = head[u];i;i=G[i].next){
if(dis[v] == dis[u] + 1 && G[i].cap){
int x = dfs(v,min(f,G[i].cap));
f -= x;ret += x;
G[i].cap -= x;
G[i^1].cap += x;
if(f == 0) break;
}
}return ret;
}
inline int dinic(){
int ret = 0;
while(bfs()) ret += dfs(S,inf);
return ret;
}
#undef v
inline bool ca(int x,int y){
int id = (x + 1) >> 1;
if(id & 1) return (y&1) == 1;
else return (y & 1) == 0;
}
inline bool cb(int x,int y){
int id = (x + 1) >> 1;
if(id & 1){
if((y & 1) == 1) return false;
return (x & 1) == 1;
}else{
if((y & 1) == 0) return false;
return (x & 1) == 0;
}
}
inline bool cc(int x,int y){
int id = (x + 1) >> 1;
if(id & 1){
if((y & 1) == 1) return false;
return (x & 1) == 0;
}else{
if((y & 1) == 0) return false;
return (x & 1) == 1;
}
}
int d1[3][2] = {{-1,0},{0,1},{0,-1}};
int d2[3][2] = {{1,0},{0,1},{0,-1}};
map<pa,int>mp;
struct Node{
int x,y,w;
}p[maxn];
int main(){
int C,R,n;read(C);read(R);read(n);
S = maxn - 5;T = S + 1;
rep(i,1,n){
read(p[i].x);read(p[i].y);read(p[i].w);
mp[make_pair(p[i].x,p[i].y)] = i;
if(cb(p[i].x,p[i].y)) insert(S,i,p[i].w);
if(cc(p[i].x,p[i].y)) insert(i,T,p[i].w);
}
rep(i,1,n){
if( (p[i].x & 1) && ca(p[i].x,p[i].y)
&& (mp.count(make_pair(p[i].x+1,p[i].y)))){
rg j = mp[make_pair(p[i].x+1,p[i].y)];
if(p[i].y & 1){
insert(i,j,min(p[i].w,p[j].w));
rep(k,0,2){
rg nx = p[i].x + d1[k][0];
rg ny = p[i].y + d1[k][1];
if(!mp.count(make_pair(nx,ny))) continue;
insert(mp[make_pair(nx,ny)],i,inf);
}
rep(k,0,2){
rg nx = p[j].x + d2[k][0];
rg ny = p[j].y + d2[k][1];
if(!mp.count(make_pair(nx,ny))) continue;
insert(j,mp[make_pair(nx,ny)],inf);
}
}else{
insert(j,i,min(p[i].w,p[j].w));
rep(k,0,2){
rg nx = p[i].x + d1[k][0];
rg ny = p[i].y + d1[k][1];
if(!mp.count(make_pair(nx,ny))) continue;
insert(i,mp[make_pair(nx,ny)],inf);
}
rep(k,0,2){
rg nx = p[j].x + d2[k][0];
rg ny = p[j].y + d2[k][1];
if(!mp.count(make_pair(nx,ny))) continue;
insert(mp[make_pair(nx,ny)],j,inf);
}
}
}
}
int ans = dinic();
printf("%d\n",ans);
return 0;
}
老 C 的键盘
题目大意:
有一个n的排列对于每个位置i,给出[i/2]与i位置上的数的大小关系,求可能的排列数.
n <= 100
题解:
不难发现实际上这是一棵树.
我们把这棵树建出来,那么现在变成一给定一棵树,树上的边代表的父子的大小关系.
我们考虑树归 : 设\(f[i][j]\)表示在以i为根的子树内根作为排名为j的值出现的排列数.
那么问题就在于状态的合并更新了.
对于一个\(f[u][]\)要将儿子的状态\(f[v][]\)合并进来,我们首先分情况讨论:
- u的值必须 > v的值:
我们想象成两个排列进行合并.
我们知道我们必须满足的条件即v在u的前面.
那么我们枚举一下需要有多少排在u的前面即可.
由于需要保证相对顺序不发生变化,所以将n个数插到m个数中的方案即:\(C_{n+m-1}^m\)
但是由于这里要么前面能插,要么后面能插,即什么时候都多一个可以插的位置,
所以实际上这里插入的方案数为\(C_{n+m}^m\)
这样我们列出转移方程:
- u的值必须 < v的值:
相应地列出方程:
预处理前缀后缀和可以将sigma消掉.
据说这么做复杂度是\(O(n^2\log n)\)的..我也不知道为什么..
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
inline void read(int &x){
x=0;static char ch;static bool flag;flag = false;
while(ch=getchar(),ch<'!');if(ch == '-') ch=getchar(),flag = true;
while(x=(x<<1)+(x<<3)+ch-'0',ch=getchar(),ch>'!');if(flag) x=-x;
}
#define rg register int
#define rep(i,a,b) for(rg i=(a);i<=(b);++i)
#define per(i,a,b) for(rg i=(a);i>=(b);--i)
const int maxn = 128;
const int mod = (1e9 + 7);
struct Edge{
int to,next,type;
}G[maxn<<1];
int head[maxn],cnt;
void add(int u,int v,int d){
G[++cnt].to = v;
G[cnt].next = head[u];
head[u] = cnt;
G[cnt].type = d;
}
int C[maxn][maxn];
inline void prework(int n){
C[0][0] = 1;
rep(i,1,n) rep(j,0,n){
C[i][j] = C[i-1][j];
if(j != 0) C[i][j] += C[i-1][j-1];
if(C[i][j] >= mod) C[i][j] -= mod;
}
}
int f[maxn][maxn],pre[maxn][maxn],suf[maxn][maxn];
inline void init(){
memset(head,0,sizeof head);
cnt = 0;
}
int siz[maxn],n;
#define v G[i].to
void dfs(int u,int fa){
siz[u] = 1;
for(int i = head[u];i;i=G[i].next){
if(v == fa) continue;
dfs(v,u);siz[u] += siz[v];
}
rep(i,2,n) f[u][i] = 0;
f[u][1] = 1;
rg s = 1;
static int g[maxn];
for(int i = head[u];i;i=G[i].next){
if(v == fa) continue;
rep(j,1,s+siz[v]) g[j] = 0;
if(G[i].type == -1){
rep(j,1,s) rep(k,1,siz[v]){
g[j+k-1] += 1LL*C[j+k-2][k-1]*C[s-j+siz[v]-k+1][s-j]%mod*f[u][j]%mod*suf[v][k]%mod;
if(g[j+k-1] >= mod) g[j+k-1] -= mod;
}
}else{
rep(j,1,s) rep(k,1,siz[v]){
g[j+k] += 1LL*C[j+k-1][k]*C[s-j+siz[v]-k][s-j]%mod*f[u][j]%mod*pre[v][k]%mod;
if(g[j+k] >= mod) g[j+k] -= mod;
}
}
rep(j,1,s + siz[v]) f[u][j] = g[j];
s += siz[v];
}
rep(i,1,n){
pre[u][i] = pre[u][i-1] + f[u][i];
if(pre[u][i] >= mod) pre[u][i] -= mod;
}
per(i,n,1){
suf[u][i] = suf[u][i+1] + f[u][i];
if(suf[u][i] >= mod) suf[u][i] -= mod;
}
return ;
}
#undef v
inline void work(){
init();read(n);
rg u,v;char ch;
rep(i,2,n){
u = i>>1;
while(ch=getchar(),ch<'!');
v = i;
if(ch == '<') add(u,v,-1),add(v,u,1);
else add(u,v,1),add(v,u,-1);
}
dfs(1,1);
int ans = 0;
rep(i,1,n){
ans += f[1][i];
if(ans >= mod) ans -= mod;
}
printf("%d\n",ans);
}
int main(){
int T;T = 1;
prework(100);
while(T--) work();
return 0;
}