数据结构--单调栈--求最大子矩阵的大小

求最大子矩阵的大小
给定一个整型矩阵map， 其中的值只有0和1两种， 求其中全是1的所有矩形区域中， 最大的矩形区域为1的数量。
例如：
1 1 1 0
其中， 最大的矩形区域有3个1， 所以返回3。
再如：
1 0 1 1
1 1 1 1
1 1 1 0
其中， 最大的矩形区域有6个1， 所以返回6。

解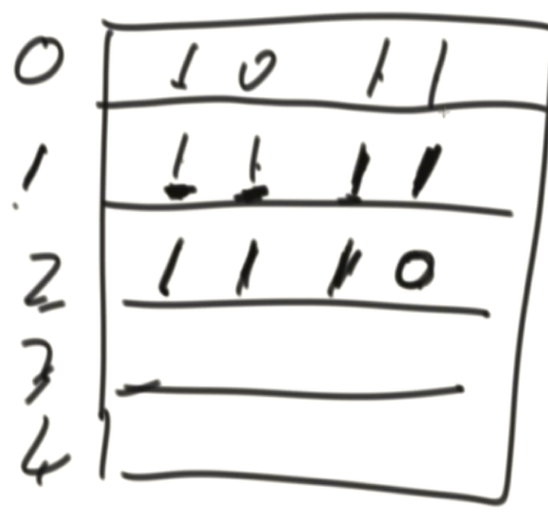：将其放到一个矩阵中，同时从第0行开始计算，以该行打底时，直方图的最大面积

如第0行，数组为[1, 0, 1, 1] 此时按照下面的求直方图最大面积。

然后以第1行打底，此时数组为[2, 1, 2, 2]，同理求直方图最大面积

然后以第2行打底，此时数组为[3, 2, 3, 0] 

注：数组的大小是按照它这一行开始，一列中有多少个连续的1来计算的。

 

 

类似的题目：给定一个数组，表示的是每个位置的直方图的高度，求直方图中连续部分的最大面积

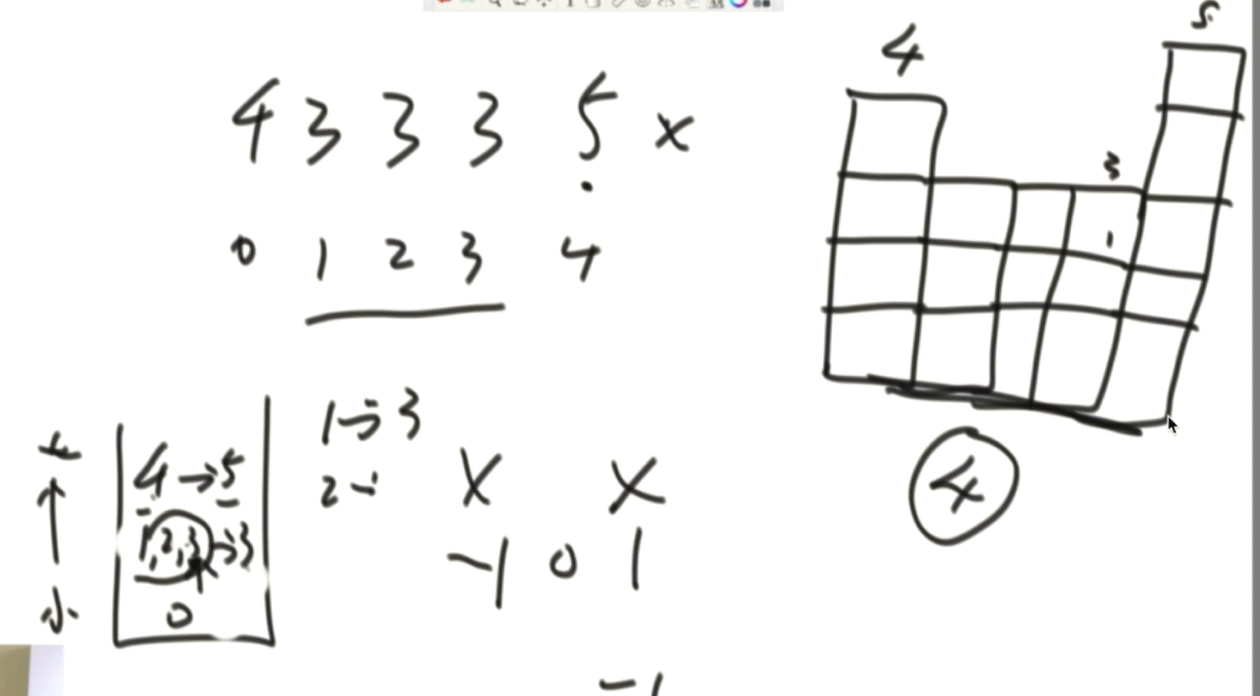
解：利用单调栈，构成一个有栈底到栈顶是从小到大的结构，当要入栈的元素num小于栈顶元素时，栈顶元素出栈，同时对该元素左右能到达的边界进行记录，这样以这个元素为中心的面积就可以求出来了。

 

package dataStructure.stack;

import java.util.Stack;

/**
 * Created by Skye on 2018/5/3.
 * 利用单调栈结构，从栈底到栈顶是从小到大的顺序
 * 以每一行为底，能组成的最大的面积，
 * 遍历每一行时，都要计算，从该位置到左到右比它小的最近的元素的位置，
 * 然后求出这两个位置之间的间距 * 当前位置的高度 就是此位置能够成的最大面积
 *
 */
public class MaximalRectangle {

    public static int maxRectangle(int[][] arrays){
        if(arrays == null || arrays.length == 0 || arrays[0].length == 0) return 0;
        int res = 0;
        int[] help = new int[arrays[0].length];
        for(int i = 0; i < arrays.length; i++){
            Stack<Integer> stack = new Stack<>();
            for(int j = 0; j < arrays[i].length; j++){
                help[j] = arrays[i][j] == 0 ? 0 : help[j] + arrays[i][j];
            }
            for(int j = 0; j < help.length; j++){
                while(!stack.isEmpty() && help[stack.peek()] > help[j]){
                    int right = j;
                    int num = stack.pop();
                    int left = stack.isEmpty() ? -1 : stack.peek();
                    res = Math.max(help[num] * (right - left - 1), res);
                }
                stack.push(j);
            }
            while(!stack.isEmpty()){
                int right = help.length;
                int num = stack.pop();
                int left = stack.isEmpty() ? -1 : stack.peek();
                res = Math.max(help[num] * (right - left - 1), res);
            }
        }
        return res;
     }

    public static void main(String[] args) {
        int[][] map = { { 1, 0, 1, 1 }, { 1, 1, 1, 1 }, { 1, 1, 1, 0 }, };
        System.out.println(maxRectangle(map));
    }
}