数据结构--Manacher算法(最长回文子串)
在字符串中求出其最长回文子串
可能是奇回文也可能是偶回文,要考虑全面
暴力解法:(因为存在奇回文和偶回文的问题,所以不好找,有一个技巧,就是向字符串中每个字符之间添加一个符号(任意符号,也可以是字符串中的符号),然后在每个位置向两端开始扩充)
答案就是最大值/2

判断的前期处理,在字符串的左右都加一个 #
* 11311 --> #1#1#3#1#1#
* 然后以每个字符为基础,向两边开始扩充,得到此字符的回文子串,最后返回最大的回文子串的长度 / 2
代码
public static int manacher1(String str){
if(str == null || str.length() == 0) return -1;
char[] ch = new char[str.length() * 2 + 1];
/*for(int i = 0, j = 0; i < ch.length && j < str.length(); i++){
ch[i++] = '#';
ch[i] = str.charAt( j++ );
}*/
int index = 0;
for(int i = 0; i < ch.length; i++){
ch[i] = (i & 1) == 0 ? '#' : str.charAt( index++ );
}
int max = Integer.MIN_VALUE;
for(int i = 0; i < ch.length; i++){
int count = 1;
for(int x = i - 1, y = i + 1; x >= 0 && y < ch.length; x--, y++){
if(ch[x] == ch[y]){
count += 2;
}else{
break;
}
}
max = max > count ? max : count;
}
return max;
}
Manacher算法: 字符串中每个字符串之间也要加上一个字符
回文直径:从某个位置开始向两边扩的最大长度
1. 回文半径数组:arr[],以每个位置为中心能扩出来的回文半径的长度
2. 最右回文右边界R:所有回文半径中,最靠右的位置
开始位置为-1
3. 回文右边界的中心 当前回文右边界到达最右边时,是以哪个位置为中心进行扩充的
算法:
1.当前位置为 i
可能性1:i 在回文右边界R外,则采用暴力扩充
可能性2:
①、i 在回文右边界R内,且 i 关于回文右边界中心的对称位置 i’ 的回文中心的半径 全部在L 和 R内部,
此时 i 位置的回文区域的半径和 i' 一样
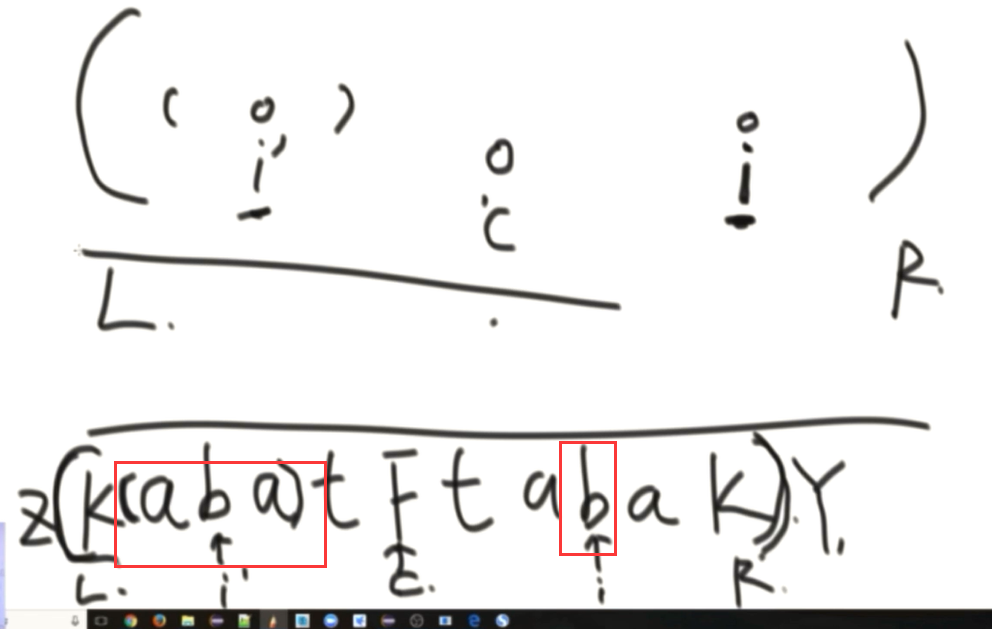
②、:i 在回文右边界R内,且 i 关于回文右边界中心的对称位置 i’ 的回文中心的半径 部分在L 和 R内部
此时 i 位置的回文半径就是 i 到 R
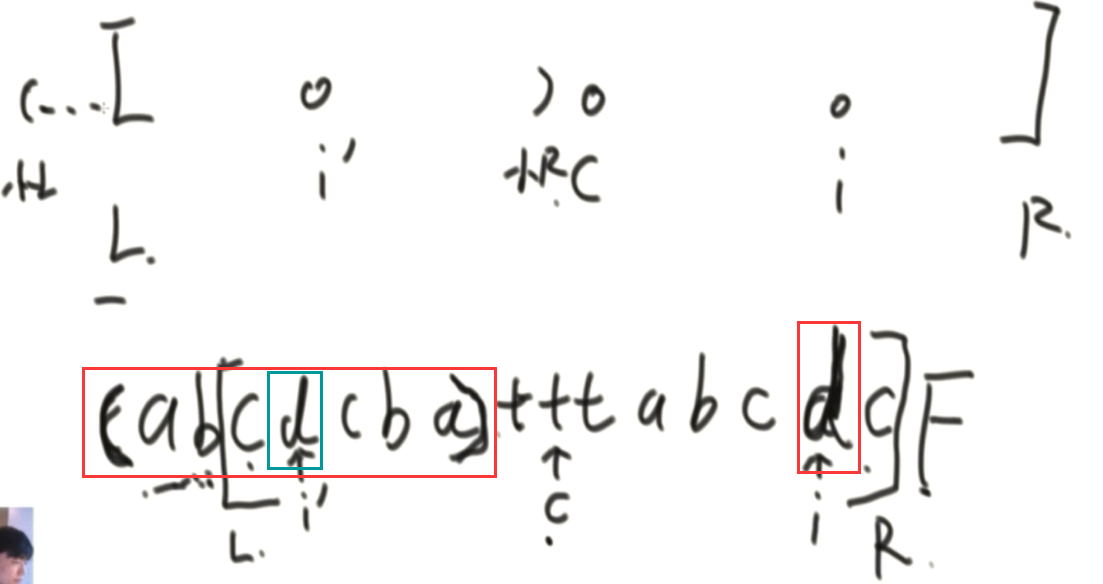
③、:i 在回文右边界R内,且 i 关于回文右边界中心的对称位置 i’ 的回文中心的半径就是L
此时 i 位置的回文半径至少是 i 到 R,后面的情况是不确定的。
①
②
③
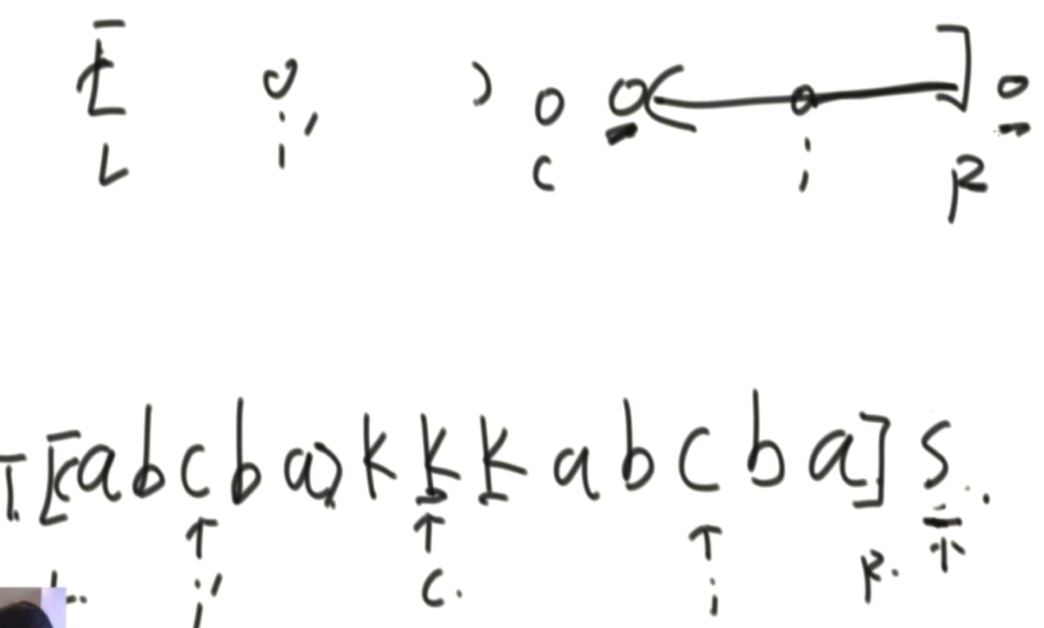

/**
* manacher算法
* 情况1:当前点 i 在最右回文右边界外面
* 采用暴力扩
* 情况2:当前点 i 在最右回文右边界里面
*
*/
public static int manacher2(String str){
if(str == null || str.length() == 0) return -1;
char[] ch = new char[str.length() * 2 + 1];
int index = 0;
//对字符串进行处理 11311 --> #1#1#3#1#1#
for(int i = 0; i < ch.length; i++){
ch[i] = (i & 1) == 0 ? '#' : str.charAt( index++ );
}
for(int i = 0; i < ch.length; i++){
System.out.print(ch[i]);
}
System.out.println();
//最右回文右边界
int maxRight = -1;
//当前回文右边界第一次出现的中心
int center = 0;
//用来记录各点的回文长度 回文半径数组
int[] flags = new int[ch.length];
int max = 0;
for(int i = 0; i < ch.length; i++){
// i 在最右回文右边界外面 暴力扩
if(i > maxRight){
int x = i - 1, y = i + 1;
while( x >= 0 && y < ch.length){
if(ch[x] != ch[y]) break;
x--;
y++;
}
maxRight = maxRight > y - 1 ? maxRight : y - 1;
center = maxRight > y - 1 ? center : i;
flags[i] = y - 1 - i;
} else{
// i 在最右回文右边界里面
//1. 其关于回文中心的对称位置 mirrorI 的回文右边界在当前最右回文右边界的里面
int mirrorI = 2 * center - i;
if(flags[mirrorI] < maxRight - i){
flags[i] = flags[mirrorI];
//2. 其关于回文中心的对称位置 mirrorI 的回文右边界在当前最右回文右边界的外面
} else if(flags[mirrorI] > maxRight - i){
flags[i] = maxRight - i;
} else{
//3. 其关于回文中心的对称位置 mirrorI 的回文右边界等于当前最右回文右边界 从maxRight处继续向外边扩
int x = i - flags[mirrorI] - 1, y = maxRight + 1;
while (x >= 0 && y < ch.length){
if(ch[x] != ch[y]) break;
x--;
y++;
}
maxRight = maxRight > y - 1 ? maxRight : y - 1;
center = maxRight > y - 1 ? center : i;
flags[i] = y - 1 - i;
}
}
max = Math.max( max, flags[i] );
}
return max;
}
优化版
public static int manacher3(String str){
if(str == null || str.length() == 0) return 0;
char[] ch = new char[str.length() * 2 + 1];
int index = 0;
for(int i = 0; i < ch.length; i++){
ch[i] = (i & 1) == 0 ? '#' : str.charAt( index++ );
}
//回文半径数组
int[] flags = new int[ch.length];
//最右回文右边界
int maxRight = -1;
//第一次取到最右回文右边界时的位置
int center = 0;
//最长回文子串长度
int max = Integer.MIN_VALUE;
for(int i = 0; i < ch.length; i++){
//判断当前 i 位置与最右回文右边界maxRight的大小,若 i 在 maxRight外部,则 当前回文半径 = 1,
// 否则当前回文半径 = i 对称点的半径 和 最右回文右边界中,较小的那个,然后,均向外扩,
// 那么 i的对称点的回文半径在maxRight外部和内部均解决,只剩下 回文半径 = maxRight情况,
// 然后以maxRight为起始点,开始向外扩
flags[i] = maxRight > i ? Math.min(flags[2 * center - i], maxRight - i) : 1;
while(i + flags[i] < ch.length && i - flags[i] >= 0){
if(ch[i + flags[i]] == ch[i - flags[i]]) {
flags[i]++;
}
else break;
}
if(i + flags[i] > maxRight){
maxRight = i + flags[i];
center = i;
}
max = Math.max( flags[i], max );
}
return max - 1;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号