贪心算法--堆--哈夫曼编码应用——切金条 （PriorityQueue 优先队列）

一块金条切成两半， 是需要花费和长度数值一样的铜板的。

比如长度为20的 金条， 不管切成长度多大的两半， 都要花费20个铜板。

一群人想整分整块金 条， 怎么分最省铜板？
例如,给定数组{10,20,30}， 代表一共三个人， 整块金条长度为10+20+30=60.

条要分成10,20,30三个部分。 如果， 先把长度60的金条分成10和50， 花费60 再把长度50的金条分成20和30，
花费50 一共花费110铜板。
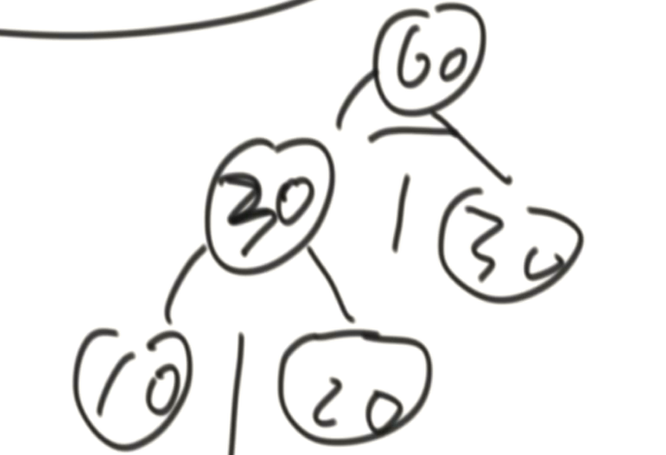
但是如果， 先把长度60的金条分成30和30， 花费60 再把长度30金条分成10和20， 花费30 一共花费90铜板。
输入一个数组， 返回分割的最小代价。

 

 

哈夫曼编码
子结点合并在一起的代价，是加起来的和

哈夫曼树的代价是所有非叶结点的和

比较器：要implements Comparator接口，然后重写compare方法

//小根堆
    public static class MinheapComparator implements Comparator<Integer>{
        @Override
        public int compare(Integer o1, Integer o2) {
            return o1 - o2;
        }
    }

    //大根堆
    public static class MaxheapComparator implements Comparator<Integer>{

        @Override
        public int compare(Integer o1, Integer o2) {
            return o2 - o1;
        }
    }

　　

cost为花费
金条总长度 len 为数组之和
按照首先构造一个小根堆，
弹出两个最小的值，求和  cost += 这两个结点的和
将和加入到小根堆中，，直到最后只剩下一个结点时停止，

代价不是最后一个值，而是所有非叶结点之和，即上面求得两两个结点之和

实际上是从底往上，逆向的计算的，实际切割却是从上往下

 

 

public static int lessMoney(int[] arrays){
        if(arrays == null || arrays.length == 0) return 0;
        //切割金条总花费
        int cost = 0;

        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
        for(int i = 0; i < arrays.length; i++){
            priorityQueue.add(arrays[i]);
        }
        while(priorityQueue.size() > 1){
            int curCost = priorityQueue.poll() + priorityQueue.poll();
            cost += curCost;
            priorityQueue.add( curCost );
        }

        return cost;
    }

整体实现

利用哈夫曼树计算切金条的花费

利用比较器构建大根堆和小根堆

 

public class LessMoney {
    //小根堆
    public static class MinheapComparator implements Comparator<Integer>{
        @Override
        public int compare(Integer o1, Integer o2) {
            return o1 - o2;
        }
    }

    //大根堆
    public static class MaxheapComparator implements Comparator<Integer>{

        @Override
        public int compare(Integer o1, Integer o2) {
            return o2 - o1;
        }
    }

    public static int lessMoney(int[] arrays){
        if(arrays == null || arrays.length == 0) return 0;
        //切割金条总花费
        int cost = 0;

        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
        for(int i = 0; i < arrays.length; i++){
            priorityQueue.add(arrays[i]);
        }
        while(priorityQueue.size() > 1){
            int curCost = priorityQueue.poll() + priorityQueue.poll();
            cost += curCost;
            priorityQueue.add( curCost );
        }

        return cost;
    }

    public static void main(String[] args) {
        // solution
        int[] arr = { 6, 7, 8, 9 };
        System.out.println(lessMoney(arr));

        int[] arrForHeap = { 3, 5, 2, 7, 0, 1, 6, 4 };

        // min heap
        PriorityQueue<Integer> minQ1 = new PriorityQueue<>();
        for (int i = 0; i < arrForHeap.length; i++) {
            minQ1.add(arrForHeap[i]);
        }
        while (!minQ1.isEmpty()) {
            System.out.print(minQ1.poll() + " ");
        }
        System.out.println();

        // min heap use Comparator
        PriorityQueue<Integer> minQ2 = new PriorityQueue<>(new MinheapComparator());
        for (int i = 0; i < arrForHeap.length; i++) {
            minQ2.add(arrForHeap[i]);
        }
        while (!minQ2.isEmpty()) {
            System.out.print(minQ2.poll() + " ");
        }
        System.out.println();

        // max heap use Comparator
        PriorityQueue<Integer> maxQ = new PriorityQueue<>(new MaxheapComparator());
        for (int i = 0; i < arrForHeap.length; i++) {
            maxQ.add(arrForHeap[i]);
        }
        while (!maxQ.isEmpty()) {
            System.out.print(maxQ.poll() + " ");
        }
    }
}